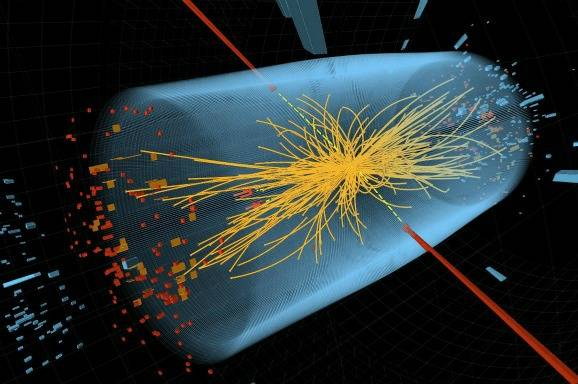
Afbeelding 1. Een meting van de LHC.De output van één meting van de Large Hadron Collider, de grote deeltjesversneller op het CERN in Genève. Aan ingewikkelde quantummechanische botsingsprocessen zoals we die hier zien, valt met geen mogelijkheid exact te rekenen. Benaderingsmethodes zoals die van de storingsreeksen spelen daarom een cruciale rol. Afbeelding: CERN.
Rekenen in de quantummechanica
Een van de pijlers van de moderne natuurkunde is de quantummechanica. Aan de hand van de quantumtheorie (zie dit dossier voor veel meer informatie over die theorie) kunnen we processen die zich op atomaire en subatomaire schaal afspelen met enorme precisie beschrijven. In een eerder artikel kwamen we al een grootheid tegen die met behulp van de quantummechanica tot meer dan tien cijfers achter de komma nauwkeurig bepaald kan worden: de gyromagnetische verhouding van het elektron.
Rekenen aan quantummechanische processen blijkt echter in het algemeen allesbehalve eenvoudig. De reden daarvoor is dat quantummechanica een theorie van kansprocessen is. In de quantummechanica is het nooit zo dat een proces maar op één manier kan verlopen; in een wat zweverige beschrijving zouden we kunnen zeggen dat de quantumwereld een ‘fuzzy’ wereld is, waarin allerlei mogelijke processen zich tegelijk afspelen – elk met een bestaande kans. Zo kan een lichtdeeltje (een foton) door twee naast elkaar liggende spleten tegelijk bewegen, kan een elektron tegelijkertijd links- en rechtsom tollen, enzovoort. Vreemd en verwarrend? In eerste instantie is het dat zeker! Wie meer over de details van deze bijzondere theorie wil begrijpen, wordt dan ook van harte aangeraden om ons uitgebreide dossier over quantumfysica te lezen.
Ook rekentechnisch maakt het kansaspect de quantummechanica wat ingewikkelder dan de klassieke natuurkundige modellen. Een experiment kan immers allerlei verschillende uitkomsten hebben; elk met een verschillende kans daarop. Wat we dus moeten uitrekenen is de verwachte, gemiddelde uitkomst van een experiment, om dat gemiddelde vervolgens te kunnen vergelijken met de meetwaarden die we in de praktijk vinden. Het moge duidelijk zijn dat het berekenen van zo’n gemiddelde – waarbij vaak ook nog eens over oneindig veel verschillende processen gemiddeld moet worden – een heel wat lastiger taak is dan het uitrekenen van één meetuitkomst. De quantummechanica is dan ook typisch een voorbeeld van een theorie waarin het zelden mogelijk blijkt te zijn om exacte uitkomsten te berekenen. Juist voor quantumproblemen zijn technieken zoals storingsrekening daarom ideaal geschikt.

Afbeelding 2. Quantummechanica en kansen.Quantummechanica is een theorie van kansen. Als we enkele lichtdeeltjes op een plaat met daarin twee spleten laten vallen, zien we op het scherm erachter (linksboven) voor elk lichtdeeltje één stip ontstaan. Pas als we heel veel lichtdeeltjes door de spleten sturen zien we dat die stippen (rechtsonder) aan een statistische verdeling voldoen. De precieze verdeling kan met behulp van de interferentie van quantumgolven exact worden uitgerekend. Afbeelding: A. Tonomura.
Quantumveldentheorie
In quantumvraagstukken is het vaak zo dat we individuele deeltjes bestuderen: de weg die één foton aflegt, of het rondtollen van één elektron. Er zijn echter ook allerlei processen in de natuur waarin meerdere deeltjes een rol spelen – denk aan botsingsprocessen. Vaak is het daarbij zelfs zo dat het aantal deeltjes in de loop van het proces kan veranderen. Zo kunnen bij botsingen met hoge energie, zoals die bijvoorbeeld op het CERN in Genève worden veroorzaakt, nieuwe deeltjes ontstaan, die vaak na zeer korte tijd ook weer uiteenvallen in andere deeltjes, of samen met een antideeltje volkomen annihileren.
Om dergelijke processen te kunnen beschrijven is een uitgebreider model nodig, dat bekend staat onder de naam quantumveldentheorie. Wie geïnteresseerd is in de details van dit model kan daarover bijvoorbeeld dit artikel lezen. In de quantumvelldentheorie wordt de wiskunde wederom wat ingewikkelder: nu is het namelijk niet alleen zo dat we gemiddeldes moeten berekenen over alle mogelijke processen die één deeltje kan doorgaan, maar dat we ook alle (wederom vaak oneindig veel) verschillende processen moeten meenemen waarin deeltjes ontstaan of verdwijnen.
Feynmandiagrammen
Laten we een heel eenvoudig quantumproces bekijken: we schieten op een bepaald punt, A, een deeltje zoals een elektron weg met een bepaalde snelheid. De vraag die we willen beantwoorden is eenvoudig: hoe groot is de kans om het deeltje na één seconde in het gebied B aan te treffen? In de klassieke natuurkunde zou die vraag eenvoudig te beantwoorden zijn: als we de beginsnelheid en -positie van het deeltje weten, beweegt het deeltje vervolgens met die snelheid langs een rechte lijn, en kunnen we dus eenvoudig uitrekenen of het deeltje wél of níet in B uitkomt. De kans is dus ofwel 100%, ofwel 0%.
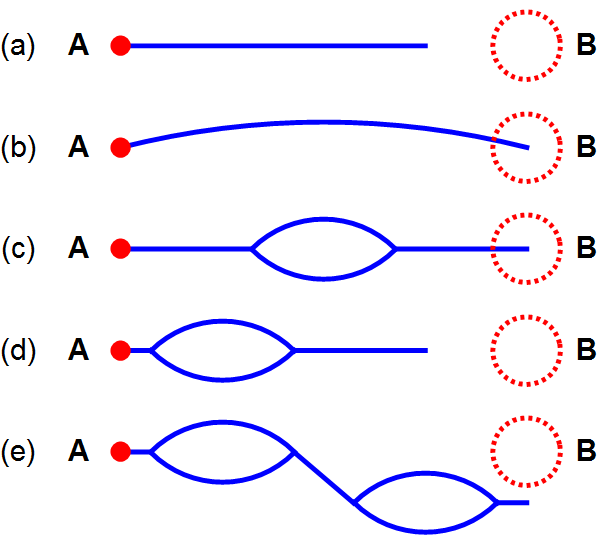
Afbeelding 3. Verschillende Feynmandiagrammen.De bovenstaande diagrammen beschrijven verschillende processen die kunnen gebeuren na het wegschieten van een quantumdeeltje uit het punt A. In sommige gevallen (b en c) komt het deeltje na een seconde in het gebied B aan; in andere gevallen niet. Soms heeft het deeltje onderweg geen interacties (a en b), soms valt een deeltje uiteen in andere deeltjes die later weer kunnen samenkomen (c en d), en soms gebeuren zulke processen zelfs meerdere malen (e).
In de quantummechanica is deze berkening een stuk ingewikkelder. Het exacte traject van het deeltje ligt immers niet vast. Er zijn allerlei verschillende trajecten mogelijk, elk met een bepaalde kans. Het traject waarin het deeltje in een rechte lijn beweegt (afbeelding 3a) zal weliswaar de grootste kans hebben, maar het is niet uitgesloten dat het deeltje in een bocht gaat (afbeelding 3b), of zelfs onderweg nieuwe deeltjes vormt, die vervolgens weer samen een nieuw deeltje kunnen worden, enzovoort (afbeelding 3c t/m 3e). We willen op élk van deze processen de kans weten, en zo de totale kans berekenen dat het deeltje in B uitkomt.
Dit is een voorbeeld van een berekening die onmogelijk exact te doen is. Gelukkig zijn er wel heel goede benaderingsmethodes, waarvan de beroemdste ontdekt werd door de Amerikaanse natuurkundige Richard Feynman. Feynman liet zien dat het heel nuttig is om alle verschillende processen eerst in te delen naar ’topologie’, oftewel de vorm van het proces. Zo zien we in afbeelding 3c en 3d twee verschillende processen waarbij de deeltjes langs iets andere trajecten bewegen, maar waarbij de topologie van het proces hetzelfde is. Het proces in afbeelding 3e heeft echter een andere toplogie: er vindt twee maal de vorming en annihilatie van een deeltjespaar plaats, in plaats van eenmaal.
Wat Feynman voorstelde is om eerst alle processen door te rekenen waarvan het interactiediagram dezelfde toplogie heeft. Zo kunnen we bijvoorbeeld eerst de kans uitrekenen dat het deeltje in B terechtkomt als er onderweg géén deeltjes ontstaan of verdwijnen. Die berekening is nog altijd niet eenvoudig, maar al een stuk eenvoudiger dan het meerekenen van alle mogelijke processen. Vaak is een dergelijke berekening met ofwel de nodige gecompliceerde integralen, ofwel de hulp van een computer, nog uitvoerbaar.
Vervolgens kunnen we bijvoorbeeld alle processen bekijken waarin één deeltjespaar ontstaat en weer verdwijnt, zoals in afbeelding 3c en 3d. Daarna rekenen we de processen door waarin twee deeltjesparen ontstaan en verdwijden, zoals in afbeelding 3e, enzovoort.
Betekent dit niet dat we nog altijd oneindig veel berekeningen moeten doen om het exacte antwoord te vinden? Jazeker, maar het mooie is dat de achtereenvolgende bijdragen die we vinden de exacte kans steeds beter en beter zullen benaderen. Voor elk botsingsproces is er namelijk een bepaalde natuurconstante die bepaald hoe sterk de interachte tussen de deeltjes is – laten we die constante, die ook wel de koppelingsconstante heet, x noemen – en het blijkt dat processen met één deeltjesinteractie evenredig zijn met de getalswaarde van x, die met twee deeltjesinteracties met x2, enzovoort. De totale uitkomst van onze berekening heeft dus de vorm
A + B x + C x2 + …
waarin A, B, C, enzovoort, de bijdragen van alle processen van één bepaalde topologie zijn. Het resultaat is dus precies een storingsreeks! Om de uitkomst van deze storingsrekening te berekenen, kunnen we de berekening eenvoudigweg afkappen als we voldoende termen in de optelsom hebben meegerekend om het eindantwoord naar onze zin voldoende dicht te benaderen. Deze techniek werkt niet alleen voor heel eenvoudige vragen zoals hierboven; dit is ook precies de manier waarop bijvoorbeeld het eerder genoemde gyromagnetische moment van het elektron is berekend.

Afbeelding 4. Richard Feynman (1918-1988).Feynman ontdekte hoe de uitkomsten quantumberekeningen benaderd kunnen worden met behulp van storingsrekening. Foto: Tamiko Thiel.
Werkt resurgence?
Zoals we in onze voorgande artikelen hebben gezien is het ‘afkappen’ van de storingsreeks na een bepaald aantal termen niet altijd voldoende. Dat hangt met name af van de grootte van de koppelingsconstante x: als x een heel klein getal is, is x2 nog kleiner, x3 nog weer kleiner, enzovoort. In zo’n geval hebben we dus al snel voldoende termen in de storingsreeks verzameld. Is de getalswaarde van x echter groot, dan wordt de einduitkomst heel langzaam, of soms zelfs helemaal níet, benaderd. In zo’n geval zijn meer geavanceerde technieken nodig. We kwamer er daarvan in dit dossier al een aantal tegen: Borelsommatie en de uitbreiding daarop: resurgence.
De quantumveldentheorie is daarmee een prachtige testcase voor deze technieken. Lukt het inderdaad om met behulp van resurgence uitkomsten in quantumveldentheorieën te berekenen? Kunnen we bepaalde zaken voorspellen die de storingsrekening zelf niet kan voorspellen, zoals de solitonen en instantonen die we in het vorige artikel bespraken?
Het onderzoek naar deze vragen staat nog in de kinderschoenen. Voor eenvoudige ’toy models’ – bijvoorbeeld theorieën in minder dan drie dimensies of waarin maar enkele soorten deeltjes voorkomen, zijn de uitkomsten veelbelovend. Resurgence blijkt inderdaad allerlei fenomenen te beschrijven en voorspellen die in die modellen niet met storingsrekening te beschrijven of voorspellen zijn. Waar de ’toy models’ zo eenvoudig zijn dat ook de exacte berekeningen gedaan kunnen worden, komen de resultaten bovendien nauwkeurig overeen. De wis- en natuurkundigen zijn echter nog niet zo ver dat het toepassen van deze technieken op realistische quantumveldentheorieën, zoals het standaardmodel dat alle bekende deeltjes in de natuur beschrijft, al lukt.
Kortom: de voortekenen zijn gunstig, maar zoals zo vaak op deze website eindigen we dit dossier aan de grens van de op dit moment bekende wetenschap, en moeten we dus afsluiten met: de toekomst zal het leren!
Dit was het voorlopig laatste artikel in het dossier ‘Storingsrekening’. Op vrijdag 5 februari begint een nieuw dossier, over quantummechanische verschijnselen in de vaste-stoffysica.