Storingsrekening (2): Achilles en de schildpad

In dit artikel:

• Een oneindige optelsom
• Geen oneindige uitkomst!
• Convergente reeksen
• Divergente reeksen
• Reeksen in de natuur

Afbeelding 1. Een schildpad.Schildpadden zijn niet de snelste dieren. Toch lijkt volgens de paradox van Zeno een schildpad die begint met een kleine voorsprong elke wedstrijd van een willekeurig snelle atleet te winnen. Foto: Skitter Photo.

Een oneindige optelsom

In het vorige artikel in dit dossier zagen we hoe we bepaalde berekeningen in de natuurkunde kunnen schrijven als optelsommen, waarin de opeenvolgende termen een steeds hogere macht van een variabele x bevatten. Zulke optelsommen worden machtreeksen genoemd. De machtreeksen die we in het vorige artikel tegenkwamen, hadden een groot maar eindig aantal termen. We willen nu bekijken hoe we de paradox over Achilles en de schildpad kunnen begrijpen aan de hand van een machtreeks met oneindig veel termen.

Laten we voor het rekengemak een behoorlijk snelle schildpad nemen. Onze schildpad loopt precies half zo snel als Achilles. De schildpad krijgt bovendien precies 1 meter voorsprong. Na een bepaalde tijd heeft Achilles het punt bereikt waarop de schildpad startte. Achilles heeft dan dus een meter afgelegd; de schildpad (die half zo snel loopt) is na diezelfde tijd een halve meter verderop aangekomen.

Wanneer Achilles vervolgens deze halve meter heeft afgelegd, is de schildpad alweer een kwart meter verder. Heeft Achilles die kwart meter afgelegd, dan is de schildpad nog een achtste meter verder, enzovoort. We kunnen deze procedure zoals gezegd oneindig vaak herhalen, maar betekent dat ook dat Achilles oneindig ver moet lopen voor hij de schildpad inhaalt?

De totale afstand A die Achilles na het optellen van al deze tussenantwoorden aflegt, is

A = 1 + 1/2 + 1/4 + 1/8 + 1/16 + …

meter. Laten we weer doen wat wiskundigen graag doen, en het getal 1/2 in deze berekening vervangen door een willekeurig getal, x. Dan kunnen we de bovenstaande optelsom schrijven als

A = 1 + x + x² + x³ + x⁴ + …

Dit is precies een machtreeks zoals we die in het vorige artikel tegenkwamen, maar nu met een oneindig aantal termen. We zagen in het eerste artikel dat eenvoudige machtreeksen met een eindig aantal termen met wat trucs soms sterk vereenvoudigd kunnen worden. Is dat hier ook het geval?

Afbeelding 2. Zeno van Elea (ca. 490-430 v. Chr.)De Griekse wijsgeer Zeno van Elea bedacht de paradox van Achilles en de schildpad. De afbeelding is een gravure uit Diogenis Laertii De Vitis van Marcus Meibomius. Overigens is niet bekend of de Zeno op de afbeelding inderdaad Zeno van Elea is, of de filosoof Zeno van Citium, die zo’n anderhalve eeuw later leefde.

Naar boven

Geen oneindige uitkomst!

Laten we om de bovenstaande optelsom uit de rekenen de totale afstand die Achilles aflegt eens vermenigvuldigen met x. Als we dat met elke bijdrage aan de som doen, vinden we

A x = x + x² + x³ + x⁴ + x⁵ + …

Wanneer we deze uitkomst aftrekken van de oorspronkelijke uitdrukking voor A zelf, zien we dat alle termen tegen elkaar wegvallen, behalve de ‘1’ waarmee de uitdrukking voor A begint. Dat wil zeggen:

A – A x = 1.

Maar A – A x kunnen we ook schrijven als A(1-x), dus als we links en rechts delen door (1-x) vinden we de eenvoudige uitkomst dat

A = 1 / (1-x).

Om het oorspronkelijke probleem op te lossen, moeten we nu x = 1/2 invullen. Dat geeft een afstand A = 1 / (1/2) = 2 meter. Klopt dit antwoord? Jazeker: in de tijd dat Achilles 2 meter aflegt, heeft de schildpad immers de helft van die afstand, 1 meter, afgelegd. Op dat moment is zijn voorsprong van 1 meter dus precies verdwenen.

De belangrijke conclusie van deze berekening is: ondanks dat we het inhalen van de schildpad in oneindig veel stapjes hebben opgedeeld, betekent dat niet dat we een oneindige uitkomst vinden!

Afbeelding 3. Fotofinish?Uiteindelijk wint, zoals te verwachten viel, de hardloper Achilles toch gemakkelijk de wedstrijd van de schildpad. Foto: Alonzo Babers wint de 400-meterwedstrijd tijdens de Olympische Spelen van 1984 – fotograaf: Don Sutherland.

Naar boven

Convergente reeksen

De berekening hierboven lijkt erg op de berekening die we in het vorige artikel deden in het voorbeeld van de koning en het schaakbord. Ter herinnering: daar vonden we dat

1 + x + x² + x³ + … + x⁶³ = (x⁶⁴ – 1) / (x-1).

Om dit resultaat nog meer op het resultaat hierboven te laten lijken, kunnen we de teller en de noemer rechts ook met -1 vermenigvuldigen. De hele breuk verandert dan immers niet, en we vinden

1 + x + x² + x³ + … + x⁶³ = (1 – x⁶⁴) / (1 – x).

Stel dat we onze berekening voor x = 1/2 ook met 64 termen zouden willen uitvoeren, in plaats van met oneindig veel termen. We zien dat de bovenstaande uitkomst dan heel sterk lijkt op de uitkomst met oneindig veel termen: het enige verschil is de teller van de breuk, die in het geval met oneindig veel termen 1 is, en in het geval met 64 termen 1 – (1/2)⁶⁴. Met een rekenmachine die met voldoende grote getallen kan werken, vinden we dat (1/2)⁶⁴ bij benadering gelijk is aan 0,000000000000000000054. Met andere woorden,

1 – (1/2)⁶⁴ ≈ 0,999999999999999999946

en het eindantwoord van de berekening met 64 termen verschilt dus maar een minieme fractie van het eindantwoord in de berekening met oneindig veel termen. Het proces kan bovendien willekeurig verbeterd worden door niet 64 maar 100 of 1000 termen in de berekening mee te nemen. Het eindantwoord met oneindig veel termen wordt zo steeds beter en beter benaderd. Een machtreeks die deze eigenschap heeft, noemen we een convergente reeks.

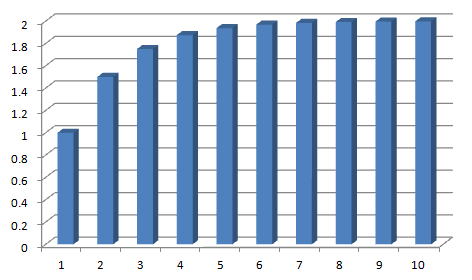
Afbeelding 4. Een convergente reeks.In deze grafiek geeft de eerste balk de grootte weer van de eerste term in het probleem van Achilles en de schildpad. De tweede balk geeft de optelsom van de eerste twee termen weer; de derde balk de optelsom van de eerste drie termen, enzovoort. We zien dat de optelsommen snel het eindantwoord 2 benaderen als het aantal termen groter wordt.

Naar boven

Divergente reeksen

Het voorbeeld van de koning en het schaakbord verschilt niet alleen van het voorbeeld van Achilles en de schildpad in de zin dat eindig veel termen door oneindig veel termen worden vervangen. De factor x, die de relatieve grootte van de opeenvolgende termen bepaalt, is ook verschillend. In het voorbeeld van Achilles en de schildpad legt de schildpad steeds de halve afstand van Achilles af; daarom gebruikten we in die berekening x = 1/2. In het voorbeeld van de koning en het schaakbord moest de koning op elk volgende veld tweemaal zoveel rijstkorrels leggen; daarom gebruikten we in dat voorbeeld x = 2.

Op fundamenteel niveau lijkt dit verschil mogelijk niet zo groot, maar dat het verschil enorm is zien we als we ook in dit geval proberen

1 + x + x² + x³ + … + x⁶³ = (1 – x⁶⁴) / (1 – x)

te benaderen door de uitkomst die we bij Achilles en de schildpad vonden:

A = 1 / (1-x).

We zien wederom dat het verschil tussen de twee uitkomsten ligt in de term x⁶⁴, maar waar die term voor x = 1/2 verwaarloosbaar klein was, vinden we voor x = 2 juist dat die term gigantisch groot wordt:

2⁶⁴ = 18.446.744.073.709.551.616.

Met andere woorden: de uitkomst met 64 termen lijkt in de verste verte niet op de formele uitkomst die we vonden voor oneindig veel termen!

De onderliggende oorzaak hiervan is de volgende. In het geval van Achilles en de schildpad, met x = 1/2, werden de opeenvolgende termen steeds kleiner: 1, 1/2, 1/4, 1/8… In het voorbeeld van de koning en het schaakbord, met x = 2, werden de opeenvolgende termen steeds groter: 1, 2, 4, 8, … In dit laatste geval is het optellen van oneindig veel termen dus onmogelijk: we willen dan oneindig veel getallen optellen, maar die getallen worden zelf ook nog eens steeds groter. Een reeks waarin de eindige sommen, als we steeds meer en meer termen meenemen, niet een bepaalde eindige waarde benaderen, noemen we een divergente reeks.

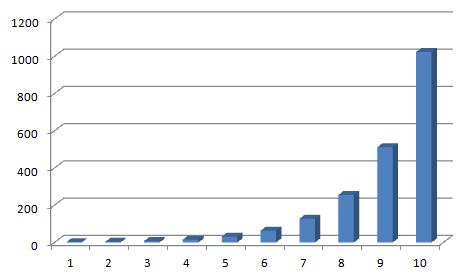
Afbeelding 5. Een divergente reeks.Een soortgelijke afbeelding als afbeelding 4, maar nu voor het voorbeeld van de koning en het schaakbord. We zien dat de optelsommen harder en harder groeien naarmate we meer termen in de berekening meenemen.

Het is nuttig om de redenering hierboven om te draaien. We hebben met formele wiskundige trucs ontdekt dat we de uitdrukking 1/(1-x) kunnen schrijven als een oneindige machtreeks:

1/(1-x) = 1 + x + x² + x³ + x⁴ + …

Aan de andere kant hebben we gezien dat de trucs alleen echt werken als x klein genoeg is: voor x = 1/2 vinden we een convergente reeks, maar voor x = 2 vinden we aan de rechterkant een reeks die divergeert. Een nauwkeuriger studie laat zien dat de reeks voor elke waarde van x tussen -1 en 1 convergeert, en voor elke waarde daarbuiten (inclusief de grensgevallen x = ±1) divergeert.

Naar boven

Reeksen in de natuur

Oneindige machtreeksen komen zoals gezegd in de natuurkunde veel voor. In de eenvoudige voorbeelden die we tot nu toe besproken hebben, konden we de machtreeks steeds zien als een manier om een bekend, exact antwoord te coderen als een som van een groot aantal – soms oneindig veel – termen. In veel natuurkundige problemen is het echter andersom: vaak weten we niet wat het exacte antwoord op een bepaalde vraag is, maar kunnen we die wel met behulp van een machtreeks benaderen. Dit is bijvoorbeeld in de quantumfysica het geval: uitkomsten van processen waarin de fundamentele natuurkrachten een rol spelen, kunnen zelden exact berekend worden, maar vaak kunnen we wel een formele oplossing in de vorm van een storingsreeks opschrijven.

De grote vraag wordt dan: convergeert of divergeert deze storingsreeks? Als de reeks convergeert, vinden we een goede benadering van het antwoord van onze berekening. Maar wat doen we als de reeks divergeert? En in welke natuurkundige systemen (er zullen er heel wat blijken te zijn!) komen we dit gedrag tegen? Dat is het onderwerp van het volgende artikel in dit dossier.

Naar boven

Het tweede artikel in dit dossier verschijnt op dinsdag 22 december.