Snaren en holografie (2): Dimensies

(Dit artikel is een herschreven versie van een eerder verschenen artikel op deze website uit oktober 2012.)

In dit artikel:

• Dimensies en coördinaten
• Minder en meer dimensies
• Dimensies in de natuurkunde
• Vlakke en gekromde dimensies

Afbeelding 1. Flatland.Het boek ‘Flatland’ van Edwin Abott Abott, verschenen in 1884. Het boek beschrijft een vierkant dat in twee dimensies leeft, en op een dag in aanraking komt met een driedimensionaal wezen.

Dimensies en coördinaten

De wereld om ons heen is driedimensionaal. Wat wil dat precies zeggen? Grofweg het volgende: we moeten in drie verschillende richtingen kunnen bewegen (van links naar rechts, van voor naar achter en van boven naar beneden) om van een willekeurig punt A naar een willekeurig punt B te gaan. Iets anders geformuleerd: we hebben drie verschillende coördinaten nodig om elk punt in onze wereld te beschrijven.

Om precies aan te geven waar ik mij in mijn huis bevind, kan ik bijvoorbeeld zeggen dat ik drie meter achter de voordeur sta, twee meter van de linkermuur, op een trapje dat een meter hoog is. Mijn coördinaten in dit (nogal willekeurige) coördinatenstelsel zijn dan dus (3m, 2m, 1m) – of als we de eenheid ‘meters’ achterwege laten: (3, 2, 1). Om te beschrijven waar de top van de Mount Everest zich bevindt, kunnen we zeggen dat die op ongeveer 28 graden noorderbreedte, 87 graden oosterlengte, en 9 kilometer hoogte ligt. Als we de eenheden weer achterwege laten kunnen we die coördinaten schrijven als (28,87,9).

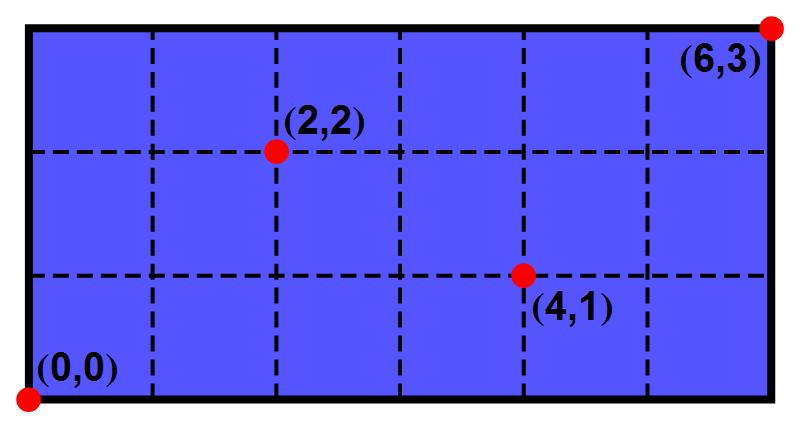
Afbeelding 2. Coördinaten.Een tweedimensionaal coördinatenstelsel. Van de vier rode punten hebben we de coördinaten aangegeven. Er zijn natuurlijk ook punten met coördinaten die geen gehele getallen zijn; die punten liggen tussen de gestippelde lijnen.

Er is in de bovenstaande voorbeelden sprake van twee heel verschillende coördinatenstelsels: één waarin we posities meten in een rechthoekig coördinatensysteem ten opzichte van de voordeur, de linkermuur en de grond; één waarin we posities meten in een bolvormig coördinatensysteem ten opzichte van de evenaar, de nulmeridiaan door Greenwich en het aardoppervlak. In beide gevallen moeten we echter drie afstanden aangeven, en hebben we dus drie coördinaten nodig.

We kunnen de noodzaak voor precies drie coördinaten nog iets anders formuleren. Elke coördinaat beperkt het aantal plaatsen waar we ons uiteindelijke doel kunnen vinden. Neem het rechthoekige coördinatenstelsel als voorbeeld. De eerste coördinaat beperkt daar het aantal mogelijke punten tot een plat vlak (alle punten die drie meter achter de voordeur liggen), de tweede coördinaat tot een lijn in dat vlak (alle punten die drie meter achter de voordeur en twee meter vanaf de linkermuur liggen), en de derde coördinaat geeft tenslotte aan welk punt op die lijn (een meter boven de vloer) we bedoelen. We zien uit deze redenering dat we niet met minder dan drie coördinaten af kunnen. Vandaar de bewering dat onze wereld driedimensionaal is.

Naar boven

Minder en meer dimensies

We kunnen ons bijvoorbeeld ook een tweedimensionale ruimte voorstellen. In zo’n ruimte zijn er maar twee mogelijke bewegingsrichtingen: denk aan het oppervlak van een vel papier, of het oppervlak van een bal. Een mier die over een dergelijk oppervlak loopt, zal alleen maar voor- en achteruit en naar links en rechts kunnen. Effectief heeft de mier dus maar twee coördinaten nodig om zijn positie te beschrijven – zijn wereld is in goede benadering tweedimensionaal. (Dit verandert natuurlijk als het blijkt te gaan om een vliegende mier, die ook in de derde dimensie kan bewegen!) Evenzo ervaart een mier die over een dun takje loopt een ruimte die in goede benadering eendimensionaal is: hij kan alleen maar voor- en achteruit lopen, en heeft aan één coördinaat voldoende om zijn positie op het takje te beschrijven.

Hoe zit het met ruimtes met meer dan drie dimensies? Die kunnen we ons een stuk lastiger voorstellen, om de simpele reden dat onze eigen wereld driedimensionaal is. We hebben in het dagelijks leven geen ervaring met vier- of hogerdimensionale ruimtes, en onze hersenen zijn dus niet goed in staat om zich zo’n wereld voor te stellen. Dat neemt niet weg dat we zo’n hogerdimensionale ruimte prima kunnen beschrijven: elk punt in zo’n ruimte kunnen we eenvoudigweg weergeven door een rijtje van vier of meer coördinaten.

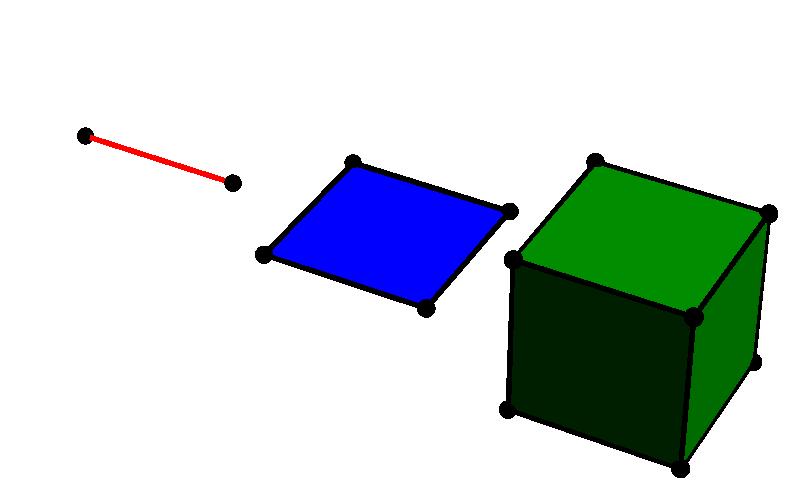
Afbeelding 3. Kubussen.‘Kubussen’ in 1, 2 en 3 dimensies.

Ook het rekenen in hogerdimensionale ruimtes is geen enkel probleem. Een voorbeeld: hoeveel hoekpunten heeft een vierdimensionale “hyperkubus”? In afbeelding 3 zien we van rechts naar links een driedimensionale kubus, een tweedimensionale ‘kubus’ (een vierkant) en een eendimensionale ‘kubus’ (een lijnstuk). We zien dat deze figuren respectievelijk 8, 4 en 2 hoekpunten hebben. Het aantal hoekpunten wordt met het verhogen van de dimensie steeds tweemaal zo groot, dus we kunnen direct al gokken dat een vierdimensionale hyperkubus 16 hoekpunten zal hebben. We kunnen dit aantal hoekpunten ook tellen, door de vierdimensionale coördinaten van de hoekpunten van een voorbeeld van zo’n hyperkubus op te schrijven:

(0,0,0,0), (0,0,0,1), (0,0,1,0), (0,0,1,1),
(0,1,0,0), (0,1,0,1), (0,1,1,0), (0,1,1,1),
(1,0,0,0), (1,0,0,1), (1,0,1,0), (1,0,1,1),
(1,1,0,0), (1,1,0,1), (1,1,1,0), (1,1,1,1).

We zien dat er inderdaad 16 hoekpunten zijn. Dit is maar een eenvoudig voorbeeld van een vierdimensionale “berekening”; met wat meer wiskunde kunnen we ook het hypervolume van een vierdimensionale bol, het aantal snijpunten van twee gekromde vlakken in vier dimensies, en nog allerlei andere meetkundige zaken berekenen.

Naar boven

Dimensies in de natuurkunde

Zijn dergelijke hogerdimensionale ruimtes alleen mysterieuze wiskundige constructies, of hebben we ze ook daadwerkelijk nodig om de natuur te beschrijven? Aangezien we in het dagelijks leven nooit meerdimensionale ruimtes tegen lijken te komen, is het antwoord misschien verbazend, maar hogerdimensionale ruimtes zijn een essentieel hulpmiddel voor de natuurkundige! Het bekendste voorbeeld is de relativiteitstheorie van Albert Einstein. Einstein liet zien dat we ruimte, tijd en zwaartekracht veel beter kunnen begrijpen als we de tijd zien als een vierde dimensie, die op gelijke voet staat met onze drie ruimtedimensies. Elke gebeurtenis in de resulterende ‘ruimtetijd‘ heeft dan vier coördinaten: drie voor de plaats waarop de gebeurtenis zich afspeelt, en een vierde voor het tijdstip. Veel meer details over de vierdimensionale ruimtetijd zijn te vinden in het dossier over de relativiteitstheorie op deze website.

Afbeelding 4. Rotaties van een kubus.Als we alleen de positie van het middelpunt van een kubus vastleggen, kunnen we de kubus nog allerlei oriëntaties geven.

Een ander voorbeeld waarin natuurkundigen meer dan drie coördinaten gebruiken, is voor het vastleggen van de volledige toestand waarin een natuurkundig systeem zich bevindt. Neem als voorbeeld een kubus die zich ergens in een kamer bevindt. Als we van die kubus alleen de drie coördinaten van het middelpunt zouden beschrijven, weten we nog niet precies in welke oriëntatie de kubus zich bevindt. We kunnen de kubus dan nog op allerlei manieren om zijn middelpunt draaien, zonder dat de positie van dat middelpunt zelf verandert – zie de animatie in afbeelding 4.

We kunnen de beschrijving van de toestand van de kubus verbeteren door ook de positie van een van zijn hoekpunten te beschrijven. Dat hoekpunt bevindt zich ergens in een bolvormige ‘schil’ rond het middelpunt; we hebben om die positie te beschrijven dus genoeg aan twee extra (bol)coördinaten. De hele positie van de kubus ligt daarmee echter nog steeds niet vast! Om dat voor elkaar te krijgen moeten we ook nog de positie van een tweede hoekpunt beschrijven. Dat hoekpunt kan nog draaien om de as door het middelpunt van de kubus en het al vastgelegde hoekpunt – zie de animatie in afbeelding 5.

Afbeelding 5. Rotaties van een kubus.Als we van de kubus ook de positie van een hoekpunt vastleggen (hier het hoekpunt rechtsonder) kan de kubus nog om één as draaien.

Om de positie van het tweede hoekpunt vast te leggen, hebben we dus nog één laatste coördinaat nodig. In totaal hebben we daarmee voor het beschrijven van de positie en oriëntatie van de kubus zes coördinaten nodig. We kunnen de toestand van de kubus dus zien als een punt in een abstracte, zesdimensionale ruimte – ook wel de “toestandsruimte” genoemd. In het dossier over faseruimtes dat deels op deze website verschenen is (en binnenkort wordt vervolgd), wordt verder beschreven waarom het nuttig kan zijn om met dergelijke hogerdimensionale toestandruimtes te werken.

Naar boven

Vlakke en gekromde ruimtes

Laten we nog twee slotopmerkingen maken over punten die vaak tot verwarring leiden. Allereerst: zoals we hebben gezien, hoeven dimensies niet altijd ‘plat’ te zijn. Het oppervlak van een vel papier is plat, maar het oppervlak van een bal of van de aarde is gekromd. Een tweedimensionale ruimte kan dus gekromd zijn, en hetzelfde geldt (hoewel we ons dit veel moeilijker kunnen voorstellen) voor drie- en hogerdimensionale ruimtes. Ook de zesdimensionale ruimte die de positie en oriëntatie van de kubus beschrijft, heeft bijvoorbeeld een aantal gekromde dimensies: de dimensies die de rotatie van de kubus om zijn middelpunt beschrijven.

Afbeelding 6. De aarde.Het oppervlak van de aarde is een tweedimensionaal, gekromd oppervlak. Ook hogerdimensionale ruimtes kunnen gekromd zijn, al kunnen wij ons die kromming veel moeilijker voorstellen. Foto: NASA.

Ten tweede: de kromming van een tweedimensionale ruimte kunnen we ons goed voorstellen, omdat we die kromming in onze derde dimensie kunnen uitbeelden. De kromming van een driedimensionale ruimte kunnen we ons niet goed voorstellen, omdat we ten minste een vierde dimensie nodig zouden hebben om die kromming uit te beelden. Een belangrijk misverstand is echter dat er altijd extra dimensies nodig zijn om andere dimensies te kunnen krommen. De zesdimensionale ruimte die de positie van de kubus beschrijft is een goed voorbeeld: deze zes dimensies zijn gedeeltelijk gekromd, maar er is geen zevende of hogere dimensie nodig om deze kromming in te laten plaatsvinden. Ruimtes kunnen dus ook ‘intrinsiek’ gekromd zijn, zonder dat daar extra dimensies voor nodig zijn.

Naar boven

In het derde artikel in dit dossier beginnen we met het bespreken van de snaartheorie.