Snaren en holografie (15): Entropie en oppervlak

In dit artikel:

• Oppervlak en entropie
• Waar bevindt de veldentheorie zich?
• Hoe bereken je de verstrengelingsentropie?
• Wat betekent dit allemaal?

Afbeelding 1. Oppervlak en volume.Rubiks kubus bestaat uit 3 x 3 x 3 = 27 kubusjes die in elke richting drie keer zo klein zijn. Het oppervlak bestaat echter uit 54 vierkantjes, terwijl het oppervlak van een klein kubusje uit 6 vierkantjes bestaat. Het oppervlak neemt dus toe met een factor 9 (3 x 3), de inhoud met een factor 27 (3 x 3 x 3). Het feit dat oppervlak minder snel toeneemt dan volume ligt aan de basis van het holografisch principe. Foto: Mike Gonzalez.

Oppervlak en entropie

Dat er een relatie is tussen quantumzwaartekracht en entropie is al lange tijd bekend. Stephen Hawking en Jacob Bekenstein ontdekten dat zwarte gaten een enorme entropie hebben (dus: een enorme hoeveelheid informatie in zich kunnen verbergen) en dat die entropie proportioneel is met het oppervlak van de rand (de horizon) van het zwarte gat. Dit was een verbazende ontdekking: we zijn in het dagelijks leven gewend dat de hoeveelheid informatie die we in een systeem kwijt kunnen proportioneel is met het volume van een systeem, en niet met het oppervlak. Als we een doos in alle richtingen drie keer zo groot maken, verwachten we dat er 3 x 3 x 3 = 27 keer zo veel informatie in past, en niet 3 x 3 = 9 keer. In de quantumzwaartekracht ‘ziet’ de entropie als het ware een dimensie te weinig.

De observatie dat entropie van een zwart gat proportioneel is met zijn oppervlak, leidde uiteindelijk tot de ontdekking van het holografisch principe. Dit principe zegt dat een theorie van de quantumzwaartekracht equivalent moet zijn met een theorie zonder zwaartekracht in één dimensie minder. Juan Maldacena vond in 1998 een eerste voorbeeld van twee theorieën die inderdaad op deze manier ‘duaal’ aan elkaar zijn: de AdS/CFT-correspondentie.

De vraag is echter: als het holografisch principe algemeen geldig is voor de quantumzwaartekracht, wat is er dan zo bijzonder aan zwarte gaten? Waarom zou alleen voor een zwart gat de hoeveelheid entropie bepaald moeten worden door het oppervlak? Zouden we niet verwachten dat in zekere zin elk zwaartekrachtssysteem dat zich in een bepaald gebied bevindt, beschreven kan worden met een entropie in een theorie in één dimensie minder, en dat die entropie op de een of andere manier gerelateerd is aan het oppervlak van het systeem? We zullen in dit artikel zien dat dat inderdaad het geval is.

Naar boven

Waar bevindt de veldentheorie zich?

Om de algemene relatie tussen oppervlak en entropie te kunnen begrijpen, moeten we iets meer weten over de relatie tussen de hogerdimensionale theorie mét zwaartekracht en de lagerdimensionale theorie zónder. Deze relatie is het meest concreet in de AdS/CFT-dualiteit van Maldacena, dus laten we kijken naar dat beroemde voorbeeld van het holografisch principe. In het artikel over de AdS/CFT-dualiteit zagen we dat Maldacena deze dualiteit afleidde door op twee verschillende manieren ‘in te zoomen’ op een systeem van open en gesloten snaren. Inzoomen op de open snaren gaf een conforme veldentheorie (CFT) in vier dimensies; inzoomen op de gesloten snaren een theorie van de quantumzwaartekracht in een vijfdimensionale anti-de Sitterruimte (AdS).

Afbeelding 2. Het hyperbolische vlak.Het hyperbolische vlak is het tweedimensionale ruimtelijke analogon van de hogerdimensionale anti-de Sitter-ruimtetijd. De afbeelding hierboven geeft een vervormde weergave van het hyperbolische vlak: in het echte hyperbolische vlak zijn alle zwarte en witte ‘driehoeken’ even groot. Het voordeel van deze weergave is dat de ‘rand’, die gemeten in het echte vlak oneindig ver weg ligt, ook in het plaatje weergegeven kan worden. Afbeelding: Anton Sherwood.

Deze procedure van ‘inzoomen’ doet vermoeden dat de twee theorieën die we vinden in zekere zin met elkaar verbonden zijn; dat we door weer terug uit te zoomen de ene theorie in de andere terug kunnen vinden. Dit vermoeden blijkt juist te zijn: het blijkt zo te zijn dat we de conforme veldentheorie kunnen zien als een beschrijving van de natuurkunde die zich op de ‘rand’ van de anti-de Sitterruimte afspeelt. Dit lijkt een vreemde constatering, aangezien een anti-de Sitterruimte net als onze eigen ruimte (voor zover we weten) oneindig groot is, en dus helemaal geen rand lijkt te hebben. Dat is ook wat we vanuit het inzoom-idee zouden verwachten: als we oneindig ver ergens op inzoomen, verwachten we dat een eventuele rand ook oneindig ver weg is. Deze redenering is in grote lijnen juist: de anti-de Sitterruimte heeft wel degelijk een rand, maar die rand is in normale afstanden gemeten oneindig ver weg. Met een wiskundige truc kunnen we echter toch de hele, oneindig grote ruimte én haar rand in één plaatje weergeven – zie afbeelding 2. Een dergelijke weergave blijkt, zoals we hieronder zullen zien, erg nuttig te zijn wanneer we sommige natuurkundige grootheden in de anti-de Sitterruimte willen omrekenen in natuurkundige grootheden in de conforme veldentheorie.

Naar boven

Hoe bereken je de verstrengelingsentropie?

Voor veel fysische grootheden blijkt juist het omrekenen vanuit de vierdimensionale theorie naar de viifdimensionale theorie (of omgekeerd) erg lastig. De AdS/CFT-dualiteit blijkt namelijk niet-locaal te zijn, wat inhoudt dat een grootheid die in de ene theorie op één punt is gedefinieerd – bijvoorbeeld de sterkte van het elektromagnetische veld op een punt in de ruimte – in de andere theorie ‘vertaald’ wordt in een enorm gecompliceerde combinatie van grootheden op allerlei verschillende punten.

De vraag hoe we grootheden in het algemeen precies vertalen van de ene naar de andere theorie, is een belangrijke onderzoeksvraag waar de laatste jaren veel werk aan is verricht. De zoektocht is daarbij met name naar grootheden die relatief makkelijk te vertalen zijn, in de hoop dat die ons meer intuïtie geven bij het opstellen van een algemeen ‘woordenboek’. Uit de voorgaande alinea blijkt dat we bij het zoeken naar dergelijke grootheden met name moeten kijken naar grootheden die niet op één plaats gedefinieerd zijn – juist grootheden die locaal zijn, zijn immers erg lastig om te zetten naar de andere theorie.

Verstrengelingsentropie – wanneer we die meten in de vierdimensionale theorie – blijkt nu een grootheid te zijn die wél betrekkelijk eenvoudig om te zetten is in een grootheid in de andere, vijfdimensionale theorie. Verstrengelingsentropie is inderdaad een grootheid die niet op één punt gedefinieerd is: verstrengelingsentropie zegt immers iets over een bepaald gebied in de vierdimensionale ruimtetijd, en over of en hoe de informatie in dat gebied verstrengeld is met de informatie in de rest van de ruimtetijd.

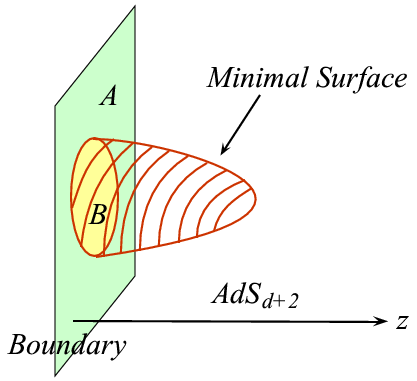
Afbeelding 3. Verstrengelingsentropie en oppervlak.Tekenen in vijf dimensies is natuurlijk erg lastig, dus het bovenstaande is een driedimensionale schets van het resultaat van het resultaat van Ryu en Takayanagi. De vierdimensionale rand van de AdS-ruimte is in deze afbeelding weergegeven als een tweedimensionaal vlak. In die rand bevindt zich een gebied B waarvan we de verstrengelingsentropie willen uitrekenen. Er zijn in de volledige vijf dimensies allerlei oppervlakken met dezelfde rand als B – het rode oppervlak is daar een voorbeeld van. Het voorschrift van Ryu en Takayanagi is nu om het kleinst mogelijke oppervlak met deze rand te vinden; de oppervlakte daarvan is gelijk aan de verstrengelingsentropie van B met A. De schets is in één opzicht misleidend: het oppervlak van het rode gebied lijkt hier duidelijk groter dan het oppervlak van B. In een anti-de Sitterruimte is het echter zo dat de oppervlakken die ‘de extra dimensie ingaan’ juist kleiner zijn dan het oorspronkelijke oppervlak, waardoor er inderdaad altijd zo’n minimaal oppervlak bestaat. (Afbeelding uit het overzichtsartikel ‘Holographic Entanglement Entropy: an Overview’ van Ryu, Takayanagi en Tatsuma Nishioka.)

Hoe verstrengelingsentropie ‘vertaald’ moet worden naar een grootheid in de vijfdimensionale theorie, werd in 2006 ontdekt door de Japanse natuurkundigen Shinsei Ryu en Tadashi Takayanagi. Het resultaat van hun onderzoek is vrij eenvoudig grafisch weer te geven als we bedenken dat we de vierdimensionale CFT kunnen zien als een theorie op de rand van de vijfdimensionale anti-de Sitterruimte – zie afbeelding 3. Stel dat we in de vierdimensionale ruimte de verstrengelingsentropie van een gebied B met de rest van de ruimte (A) willen uitrekenen. Het vierdimensionale gebied B heeft een driedimensionale rand, maar als we B zélf zien als een gebied op de rand van een vijfdimensionale ruimte, zijn er ook nog allerlei andere driedimensionale ‘oppervlakken’ in die vijfdimensionale ruimte die dezelfde rand hebben als B. (Over de terminologie: in vijf ruimtetijddimensies is een ‘oppervlak’ driedimensionaal, net zoals in onze vier ruimtetijddimensies een oppervlak tweedimensionaal is. Een zwart gat in vijf ruimtetijddimensies heeft bijvoorbeeld een driedimensionale horizon.) Het voorschrift van Ryu en Takayanagi is nu als volgt: vind in de vijfdimensionale anti-de Sitterruimte een oppervlak B’ dat dezelfde rand heeft als B, maar zó dat het oppervlak van B’ zo klein mogelijk is. De grootte van dit oppervlak blijkt exact gelijk te zijn aan de verstrengelingsentropie in B!

Naar boven

Wat betekent dit allemaal?

Het resultaat dat Ryu en Tayanagi bereikten, is in veel opzichten een heel bijzonder resultaat. Allereerst is het een mooi voorbeeld van de hierboven genoemde ‘vertaalslag’. In de ene theorie (de vierdimensionale CFT) kunnen we de verstrengelingsentropie uitrekenen; in de andere theorie (quantumzwaartekracht in een vijfdimensionale anti-de Sitterruimte) de grootte van een oppervlak, en uiteindelijk blijkt dat we in de twee theorieën exact dezelfde uitkomst vinden. Verstrengelingsentropie in vier dimensies wordt dus vertaald in een oppervlaktemaat in vijf dimensies.

Dat brengt ons direct op het tweede bijzondere punt: in de vierdimensionale CFT doen we in dit voorbeeld een quantummechanische berekening, terwijl we in de vijfdimensionale quantumzwaartekracht een meetkundige grootheid (een oppervlakte) bepalen. Dit is geheel in lijn met de filosofie achter het holografisch principe. De algemene relativiteitstheorie, waarmee we de zwaartekracht beschrijven, is een theorie die de meetkunde van de ruimtetijd beschrijft. Een berekening over deze meetkunde in de vijfdimensionale quantumzwaartekracht zou dus inderdaad vertaald moeten worden in een berekening van een quantumgrootheid in de vierdimensionale theorie, waar de quantumzwaartekracht geen rol meer speelt.

Afbeelding 4. Tadashi Takayanagi.Takayanagi legt zijn ideeën over verstrengelingsentropie en oppervlakte uit. Foto: Kyoto University.

Het derde bijzondere punt aan het resultaat van Ryu en Takayanagi, en misschien wel het meest interessante van de drie, is dat de vinding een gedeeltelijk antwoord geeft op de vraag waarmee we dit artikel begonnen. Het minimale oppervlak B’ kunnen we zien als de rand van een vrij willekeurig gebied in de vijfdimensionale ruimtetijd – B’ hoeft bijvoorbeeld beslist niet de horizon van een zwart gat te zijn. We zien nu dat de grootte van het oppervlak van zo’n algemeen gebied ook vertaald kan worden in een grootheid in een theorie met een dimensie minder – en zelfs in een entropie in die theorie. Het kernidee van holografie – het idee dat quantumzwaartekracht te beschrijven is in termen van grootheden op de rand van het gebied dat we bestuderen – blijkt dus veel algemener van toepassing dan alleen op zwarte gaten.

De verrassend belangrijke rol die het begrip entropie in dit verhaal speelt, roept natuurlijk veel vragen op. Waarom hebben entropie en zwaartekracht, twee op het oog heel verschillende begrippen, zo veel met elkaar te maken? Deze vraag is een heel belangrijke en actuele onderzoeksvraag in de moderne theoretische natuurkunde. In het komende artikel zullen we iets zeggen over een van de mogelijke antwoorden op deze vraag.

Naar boven

In het zestiende artikel in dit dossier bespreken we het verband tussen thermodynamica en zwaartekracht, en de vraag of dit verband berust op toeval of op dieperliggende fysica.