Relativiteit (6): Tijdsdilatatie

In dit artikel en het volgende willen we de gevolgen van de relativiteitstheorie voor ons begrip van ruimte en tijd nader onder de loep nemen. We beginnen met het begrip tijd: hoe ervaren verschillende waarnemers het tijdsinterval tussen twee gebeurtenissen? Na het bestuderen van de ruimtetijd in de vorige artikelen verwachten we niet meer dat twee waarnemers een dergelijk tijdsinterval noodzakelijkerwijs als even lang zullen ervaren. Kijk bijvoorbeeld eens naar afbeelding 1. We zien hierin de inmiddels vertrouwde referentiekaders van twee waarnemers: een zwarte, en een groene die ten opzichte van de zwarte met de helft van de lichtsnelheid beweegt. Verder zien we in de afbeelding met rode stippen twee gebeurtenissen aangegeven. Deze twee gebeurtenissen gebeuren voor de groene waarnemer op coördinaat x’=0 ls en op tijdstippen t’=0 s en t’=1 s. We kunnen deze gebeurtenissen bijvoorbeeld zien als twee tikken van een klok die de groene waarnemer bij zich draagt. Voor de zwarte waarnemer vinden deze twee gebeurtenissen plaats op x=0 ls en t=0 s voor de eerste tik, en op ongeveer x=0,6 ls en t=1,2 s voor de tweede tik. We zien hier weer duidelijk dat de tweede tik niet alleen op een andere plaats, maar ook op een ander tijdstip plaatsvindt. Met andere woorden, de klok die voor de groene waarnemer éénmaal per seconde tikt, lijkt voor de zwarte waarnemer langzamer te tikken!

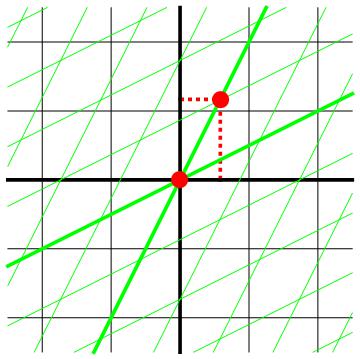
Afbeelding 1. Tijdsdilatatie.Twee tikken van een klok die de groene waarnemer met zich meedraagt vinden, van hem uit gezien, met een tijdsinterval van een seconde plaats. Voor de zwarte waarnemer komt de tweede tik pas na ongeveer 1,2 seconden, op een plaats die ongeveer 0,6 ls verschoven is. De klok lijkt voor de zwarte waarnemer dus langzamer te lopen dan voor de groene!

We kunnen ditzelfde effect nog op een andere, mogelijk meer inzichtelijke manier begrijpen. Relativiteitstheorie is gebaseerd op het feit dat licht een onveranderlijke snelheid heeft. Laten we dus een fictieve klok bouwen die gebruik maakt van het licht. Zie afbeelding 2: we nemen twee spiegels, zetten die op een afstand van 300.000 kilometer van elkaar, en laten een lichtflits tussen de twee spiegels heen-en-weerkaatsen. De “tikken” van de klok zijn de momenten waarop het lichtflitsje een van de spiegels bereikt. Door de afstand waarop we de spiegels gezet hebben, zal deze klok voor een waarnemer die ten opzichte van de klok stilstaat precies eenmaal per seconde tikken.

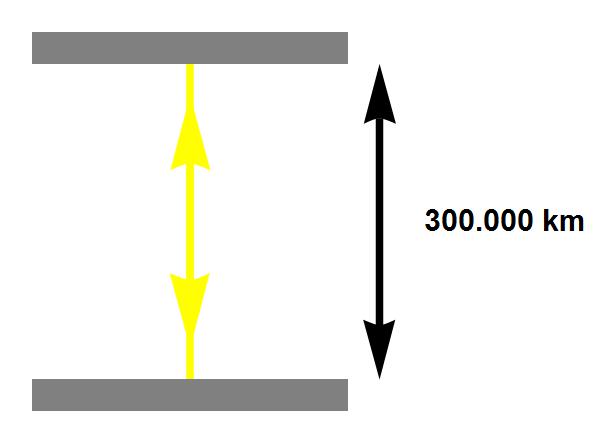
Afbeelding 2. Een lichtklok.Een lichtklok bestaat uit twee spiegels, met een onderlinge afstand van 300.000 kilometer, waartussen een lichtflits heen-en-weerkaatst. Voor een waarnemer die ten opzichte van de klok stilstaat, tikt de klok eenmaal per seconde.

Nu geven we deze klok een grote snelheid (bijvoorbeeld de helft van de lichtsnelheid) in de horizontale richting. De verticale afstand tussen de spiegels zal nog altijd 300.000 kilometer zijn, maar (zie afbeelding 3) voor een stilstaande waarnemer legt het licht tussen twee tikken een grotere, diagonale weg af. We weten echter dat de lichtsnelheid onveranderlijk is, dus het licht zal van ons uit gezien er langer over doen voor het de tweede spiegel bereikt. De tijd tussen twee tikken lijkt voor ons dus langer – we zien wederom dat de klok langzamer lijkt te lopen! Voor een waarnemer die met de klok meebeweegt gaat de lichtflits nog steeds recht op-en-neer; voor hem tikt de klok dus gewoon eenmaal per seconde.

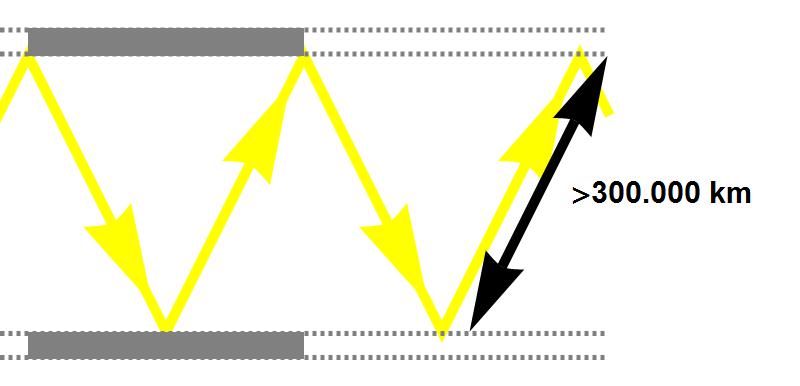
Afbeelding 3. Een bewegende lichtklok.Als de lichtklok beweegt, legt het licht tussen twee tikken een weg af die langer is dan 300.000 km. De bewegende klok tikt daardoor langzamer dan dezelfde klok in stilstand.

Wie handig is met de stelling van Pythagoras kan vrij eenvoudig zelf uitrekenen hoeveel langzamer de bewegende klok precies lijkt te lopen. Voor de liefhebbers geven we weer de formule: als het tijdsinterval tussen twee tikken van de stilstaande klok Δt is, is het tijdsinterval tussen twee tikken van de bewegende klok gelijk aan

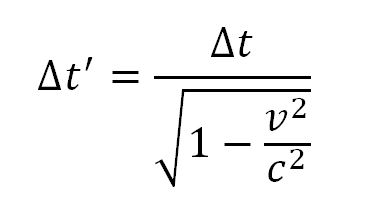
Een klok die met de helft van de lichtsnelheid beweegt, tikt bijvoorbeeld eens in de 1,15 seconden.

Het feit dat bewegende klokken langzamer lopen dan stilstaande klokken, wordt tijdsdilatatie genoemd. (In het Nieuwe Natuurkundeprogramma op de middelbare school wordt ook wel het woord tijdrek gebruikt.) In de bovenstaande afleiding van de tijdsdilatatie hebben we gebruik gemaakt van een heel bijzondere “lichtklok”. De vraag ligt voor de hand of het langzamer lopen van deze klok als hij beweegt, niet een gevolg is van de speciale constructie die we hebben gebruikt. Dat dit niet het geval is, blijkt bijvoorbeeld uit afbeelding 1, waar we hetzelfde effect zagen zonder gebruik te maken van een bepaald type klok. Een andere manier om in te zien dat het type klok niet van belang is, is door een ander soort klok, die even snel loopt, naast de lichtklok te houden. Voor de met de klokken meebewegende waarnemer zijn beide klokken niet in beweging, en lopen ze dus even snel. Elke keer dat de lichtflits onderaan de lichtklok komt, tikt ook de andere klok. Dit zijn gebeurtenissen die vlak naast elkaar op hetzelfde moment gebeuren, en die dus ook voor de niet bewegende waarnemer gelijktijdig op vrijwel dezelfde plaats moeten gebeuren. Kortom: ook de stilstaande waarnemer ziet de lichtklok en de andere klok even snel lopen. Ook de gewone klok loopt dus in beweging langzamer; niet alleen de lichtklok!

Het langzamer lopen van bewegende klokken is een van de gevolgen van de relativiteitstheorie die sterk tegen onze intuïtie indruist. De vraag is dus: kunnen we ook experimenteel testen of tijdsdilatatie een werkelijk bestaand verschijnsel is? Dat kan zeker: in 1971 voerden Joseph C. Hafele en Richard E. Keating een experiment uit waarbij atoomklokken met commerciële vliegtuigen werden meegestuurd. Na tweemaal rond de wereld te zijn gevlogen, werden de klokken vergeleken met klokken die in het laboratorium waren achtergebleven . De klokken die hadden bewogen bleken inderdaad achter te lopen.

Afbeelding 4.Joseph Hafele en Richard Keating met een van de atoomklokken die in een vliegtuig rond de wereld werd gestuurd. Foto: Time Magazine, 18 oktober 1971.

Een andere leuke manier waarop we tijdsdilatatie kunnen waarnemen, is aan de hand van muonen – geladen elementaire deeltjes die hoog in de atmosfeer ontstaan doordat kosmische straling de dampkring binnendringt. Muonen zijn instabiele deeltjes die in ongeveer anderhalve microseconde uiteen vallen in andere elementaire deeltjes. Iets preciezer: na anderhalve microseconde is de helft van de muonen vervallen, na nog eens anderhalve microseconde de helft van de overgebleven muonen, enzovoort. Deze zogenaamde halfwaardetijd is zo kort dat we zouden verwachten dat in hun reis door de atmosfeer vrijwel alle muonen vervallen. Doordat de muonen zo snel bewegen, zorgt de tijdsdilatatie er echter voor dat ook de “interne klok” van een muon veel langzamer loopt. Er komen daardoor veel meer muonen op het aardoppervlak aan dan we zonder tijdsdilatatie zouden verwachten. Dit effect werd al in 1941 voor het eerst gemeten door B. Rossi en D. B. Hall. Zij vergeleken de hoeveelheid muonen die arriveerden op de top van een hoge berg met de hoeveelheid die aankwam aan de voet van de berg, en vonden dat het resultaat in overeenstemming was met wat we zouden verwachten op basis van de tijdsdilatatie, maar enorm afweek van de verwachtingen als daarin de tijdsdilatatie niet werd meegenomen.

Deze en nog vele andere experimenten tonen aan dat tijdsdilatatie die de relativiteitstheorie voorspelt bij hoge snelheden inderdaad plaatsvindt. Tijdsintervallen zijn waarnemerafhankelijk. Laten we nu eens kijken naar het analoge effect voor ruimtelijke afstanden. Zijn die ook afhankelijk van de waarnemer die ze meet?

Dit is het zesde artikel uit het dossier Relativiteitstheorie. In het zevende artikel zien we hoe naast de tijd ook de ruimte heel bijzondere eigenschappen heeft in de relativiteitstheorie.

Foto blokkenschema: Jürgen Götzke.