Relativiteit (2): De lichtsnelheid

Hoewel het er op het eerste gezicht niet op lijkt, heeft licht een bepaalde snelheid. Als je een lamp in een kamer aandoet lijkt de hele kamer instantaan verlicht te worden, maar in werkelijkheid doet het licht er een fractie van een seconde over om vanaf de lamp de voorwerpen in de kamer te bereiken, en vanaf daar weerkaatst te worden naar je ogen. We merken daar weinig van doordat de snelheid van het licht zo enorm groot is: lichtgolven planten zich voort met bijna 300.000 kilometer per seconde. Alleen op astronomische schaal merk je iets van het feit dat het licht niet oneindig snel beweegt: zo doet het licht van de maan Hoewel het er op het eerste gezicht niet op lijkt, heeft licht een bepaalde snelheid. Als je een lamp in een kamer aandoet lijkt de hele kamer instantaan verlicht te worden, maar in werkelijkheid doet het licht er een fractie van een seconde over om vanaf de lamp de voorwerpen in de kamer te bereiken, en vanaf daar weerkaatst te worden naar je ogen. We merken daar weinig van doordat de snelheid van het licht zo enorm groot is: lichtgolven planten zich voort met bijna 300.000 kilometer per seconde. Alleen op astronomische schaal merk je iets van het feit dat het licht niet oneindig snel beweegt: zo doet het licht van de maan er ruim een seconde over om ons te bereiken, en dat van de zon zo’n acht minuten. Het licht van verre sterrenstelsels kan zelfs miljarden jaren onderweg zijn voor het ons bereikt.er ruim een seconde over om ons te bereiken, en dat van de zon zo’n acht minuten. Het licht van verre sterrenstelsels kan zelfs miljarden jaren onderweg zijn voor het ons bereikt.

Afbeelding 1. James Clerk Maxwell.James Clerk Maxwell (1831-1879), die de wiskundige beschrijving van het elektromagnetisme (en dus ook het licht) afleidde. (Gravure van G. J. Stodart, naar een foto van Fergus of Greenack.)

De natuurkundige beschrijving van het licht is afkomstig van James Clerk Maxwell. Rond 1860 leidde hij een aantal wiskundige formules af – tegenwoordig bekend als de Maxwellvergelijkingen – die heel nauwkeurig de eigenschappen van elektromagnetische golven beschrijven. Het licht is zelf zo’n elektromagnetische golf (net zoals bijvoorbeeld radiostraling en gammastraling) , en met behulp van de Maxwellvergelijkingen kunnen we dus precies de eigenschappen van het licht in natuurkundige experimenten voorspellen.

Eén eigenschap van het licht lijkt daarbij nogal verbazend: uit de Maxwellvergelijkingen volgt dat het licht voor elke waarnemer dezelfde snelheid zou moeten hebben! Dat die eigenschap indruist tegen onze intuïtie over snelheden blijkt als we het licht vergelijken met bijvoorbeeld een kogel die uit een pistool komt. Stel dat zo’n kogel op ons wordt afgevuurd met een snelheid van 300 meter per seconde. We kunnen proberen de kogel te ontwijken, of – als we het minder slim aanpakken – voor de kogel uit te rennen zodat die ons niet inhaalt. Als we met een flinke sprintsnelheid van zo’n 10 meter per seconde voor de kogel uitrennen, verwachten we dat de kogel ons met “slechts” 300-10=290 meter per seconde bereikt. Dit zien we in afbeelding 2 en 3 schematisch weergegeven – merk op dat ook hierbij weer het relativiteitsbeginsel een belangrijke rol speelt!

Afbeelding 2.Een pistool vuurt een kogel af op de groene waarnemer, die met grote snelheid van de kogel wegrent.

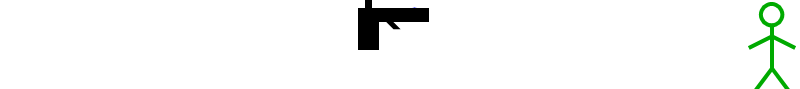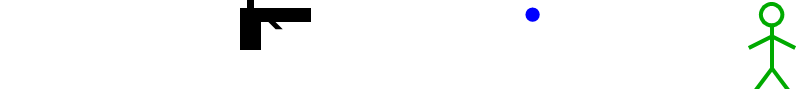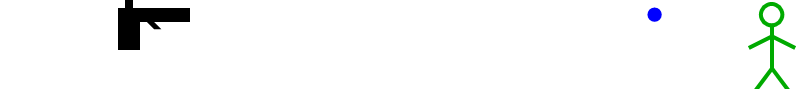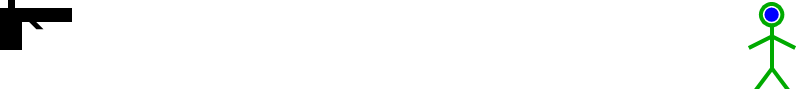
Afbeelding 3.Dezelfde situatie als in afbeelding 6, zoals waargenomen door de bewegende waarnemer. De kogel komt met een lagere snelheid op hem af; we verwachten dat die snelheid gelijk is aan de snelheid van de kogel min de snelheid van de waarnemer.

Geldt dezelfde redenering ook voor licht? We vervangen het pistool nu door een lamp, die een lichtflits op ons afstuurt met 300.000 km/s. We willen de lichtflits voor blijven, en vliegen met behulp van een supersnel ruimteschip daarom met een gigantische snelheid van 10.000 km/s van de lamp weg. Met precies dezelfde redenering als hierboven zouden we nu verwachten dat het licht ons inhaalt met een snelheid van 290.000 km/s.  Maar de Maxwellvergelijkingen voorspellen iets anders: die zeggen dat we het licht, zelfs als we weg bewegen, altijd met 300.000 km/s op ons af zullen zien komen!

Er moet dus óf iets mis zijn met onze intuïtie over snelheden (en in het bijzonder het optellen en aftrekken daarvan), óf met de wetten van Maxwell. Natuurkunde is altijd gebaseerd op onze experimenten en ervaringen, en dus gaan natuurkundigen er meestal in eerste instantie vanuit dat onze intuïtie juist is. De eerste vraag die men zichzelf stelde was dus: kan er iets mis zijn met de Maxwellverglijkingen, en kunnen we die “repareren” zodat ze weer met onze intuïtie in overeenstemming zijn?

Een oplossing die voor de hand lag was de volgende. Het zou natuurlijk goed kunnen dat de lichtgolven zich voortplanten door een bepaald medium, net zoals watergolven zich voortplanten door het water. Zo’n medium was nooit waargenomen (het licht leek zich ook prima door volkomen lege ruimte voort te planten), maar het kreeg toch alvast een naam: ether. Als het licht zich als golf door de ether voortplant, zouden de wetten van Maxwell alleen geldig zijn voor waarnemers die stilstaan ten opzichte van die ether. De uit die vergelijking volgende lichtsnelheid van 300.000 km/s zou dan ook alleen gemeten worden door waarnemers die stil staan ten opzichte van die ether, en niet door iedere willekeurige waarnemer. De wetten van Maxwell zouden daarmee incompleet zijn, en moeten worden aangevuld met wetten die ook de mogelijke bewegingen van de ether beschrijven. Samen zouden die nieuwe natuurwetten dan volgens het relativiteitsbeginsel weer voor iedere eenparig bewegende waarnemer moeten gelden.

Een dergelijke ether werd echter nooit gevonden – het leek erop dat de Maxwellvergelijkingen compleet waren, en ook de voortplanting van het licht door een volkomen lege ruimte beschreven. Dit volgde bijvoorbeeld uit een beroemd experiment dat de natuurkundigen Albert Michelson en Edward Morley in 1887 uitvoerden. In afbeelding 4 zien we een schets van dit experiment. Licht wordt afgevuurd op een half doorlatende spiegel, en komt vervolgens via twee verschillende, loodrecht op elkaar staande banen, terecht op een scherm. Aangezien licht een golf is vertoont het interferentie: als de twee lichtstralen die op het scherm vallen allebei tegelijk op een “top” van de golf zijn, versterken ze elkaar; als de ene straal op een “top” is als de ander in een “dal” is, zwakken ze elkaar juist af. Het gevolg is dat op het scherm een interferentiepatroon te zien is als in afbeelding 5.

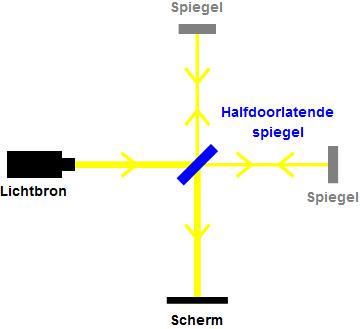
Afbeelding 4. Een schets van het experiment van Michelson en Morley.

Of de lichtstralen op een “top” of in een “dal” zijn als ze aankomen, hangt af van hoe lang de lichtstralen onderweg zijn geweest tussen het moment waarop ze in de halfdoorlatende spiegel gescheiden worden en het moment waarop ze in de detector aankomen. Als er een ether is hangt deze reistijd af van de beweging van het licht ten opzichte van de ether: stroomt de ether met het licht mee, dan gaat het licht wat sneller; stroomt de ether tegen het licht in, dan gaat het licht wat langzamer. De aarde draait in een baan rond de zon; we verwachten dus dat het licht in de bewegingsrichting van de aarde tegen de ether in stroomt, en in de omgekeerde bewegingsrichting met de ether mee. Wat Michelson en Morley nu deden was eenvoudigweg hun opstelling draaien: als er een ether zou zijn waardoorheen de aarde bewoog zouden de reistijden van het licht moeten veranderen, en zou dus ook het in de detector waargenomen interferentiepatroon moeten veranderen. Een dergelijke veranderig werd echter niet waargenomen, en dus leek het bestaan van een ether vrijwel uitgesloten.

Afbeelding 5. Interferentie.Een interferentiepatroon zoals dat op het scherm ontstaat in het experiment van Michelson en Morley.

Om het bestaan van een ether helemaal uit te sluiten, moeten er natuurlijk nog allerlei andere experimenten gedaan worden. Zo moet er bijvoorbeeld worden uitgesloten dat de aarde de ether “met zich meesleept”, zodat een draaiing van de opstelling van Michelson en Morley de snelheid van het licht ten opzichte van de ether niet verandert. Ook kan het geen kwaad om soortgelijke experimenten in een bewegend ruimteschip in de ruimte uit te voeren, om te zien of ook ver van de aarde dezelfde resultaten worden gevonden. Zulke experimenten zijn in de afgelopen ruime eeuw in overvloede gedaan, en steeds met hetzelfde resultaat: de ether lijkt niet te bestaan. Ook andere pogingen om de Maxwellvergelijkingen aan te passen leverden niets op: de vergelijkingen lijken onder alle denkbare omstandigheden te gelden.

Daarmee zijn we weer terug bij het oorspronkelijke probleem. Als de Maxwellvergelijkingen kloppen en volledig zijn, moeten ze voor elke eenparig bewegende waarnemer gelden – en moet elke eenparig bewegende waarnemer dus dezelfde lichtsnelheid waarnemen. Dit druist, zoals we eerder beschreven, rechtstreeks in tegen onze dagelijkse intuïtie over het bepalen van relatieve snelheden – we zijn gewend daarvoor eenvoudigweg snelheden op te tellen of af te trekken. Er lijkt dus iets mis te zijn met onze intuïtie!

Merk overigens op dat het onveranderlijk zijn van de lichtsnelheid niet indruist tegen het relativiteitsbeginsel. Integendeel: er lijkt een natuurwet te zijn die eenvoudigweg zegt “de lichtsnelheid is 300.000 km/s”; een natuurwet die voor elke eenparig bewegende waarnemer geldt. We zouden dus het onveranderlijk zijn van de lichtsnelheid juist kunnen zien als een mooie bevestiging van het relativiteitsbeginsel.

De vraag is natuurlijk: waar gaat onze intuïtie dan de mist in? Deze vraag werd door Einstein op een verbazend elegante wijze beantwoord. Hij nam het relativiteitsbeginsel en de onveranderlijkheid van de lichtsnelheid als uitgangspunt, en leidde af wat deze twee postulaten betekenden voor ons begrip van snelheid. Een snelheid is een afstand die wordt afgelegd in een bepaalde tijd, dus om snelheden goed te begrijpen moeten we beter kijken naar de eigenschappen van ruimte en tijd. Dit was precies wat Einstein deed. Hij kwam tot een verbazende conclusie: ruimte en tijd moeten worden samengevoegd tot één begrip: de ruimtetijd. Voor we overgaan op het beschrijven van die ruimtetijd kijken we in het volgende artikel eerst nog iets beter naar onze “klassieke” beschrijving van ruimte en tijd. Als we goed begrijpen waarop die intuïtie gebaseerd is, kunnen we ook begrijpen wat er in Einsteins visie precies verandert.

Dit is het tweede artikel uit het dossier Relativiteitstheorie. In het derde artikel beschrijven we de Galileitransformaties, die weergeven hoe ruimte en tijd zich in het klassieke wereldbeeld gedragen.