Entropie (5): Entropie en thermodynamica

Entropie als thermodynamische eigenschap

Deze statistische omschrijving van entropie is tegenwoordig de meest gangbare, maar het begrip entropie werd al ontdekt halverwege de 19e eeuw – een periode waarin het bestaan van atomen nog een hypothese was waarin lang niet iedereen geloofde. Oorspronkelijk was entropie dan ook geen microscopische, statistische grootheid. De oorspronkelijke definitie van entropie ging puur uit van de macroscopische thermodynamische eigenschappen van systemen.

Afbeelding 1. Een zuigerEen cilinder gevuld met gas, afgesloten door een beweegbare zuiger (blauw).

Laten we eens kijken naar het volgende gedachte-experiment. We nemen een cilinder die wordt afgesloten door een beweegbare zuiger, en vullen die cilinder met gas – zie afbeelding 1. We klemmen nu de zuiger tijdelijk vast, zodat die niet kan bewegen. Het gas heeft oorspronkelijk dezelfde temperatuur als de omgeving, maar nu warmen we de cilinder op en meten hoeveel warmte (en dus: hoeveel energie) we op die manier aan het gas toevoegen.

Als we nu de zuiger losmaken, zal het warme gas in de cilinder uitzetten en de zuiger een stuk naar buiten duwen. De cilinder kan daarmee gebruikt worden als een bron van energie, precies zoals dat in bijvoorbeeld een automotor gebeurt. We kunnen meten hoeveel arbeid (energie) de cilinder kan leveren, bijvoorbeeld door te meten wat het grootst mogelijke gewicht is dat de zuiger een bepaalde afstand omhoog kan duwen.

Als we dit hele experiment uitvoeren in een ruimte met constante temperatuur, en we zorgen dat er nergens in het experiment warmte weglekt, is de uitkomst van het experiment niet erg verrassend. De hoeveelheid energie die de cilinder als arbeid kan leveren, blijkt precies gelijk te zijn aan de hoeveelheid energie die we als warmte aan de cilinder hebben toegevoegd. Dit is een eenvoudig voorbeeld van de Eerste Hoofdwet van de thermodynamica: energie blijft altijd behouden.

Nu passen we het experiment als volgt aan. Voordat we de zuiger van de cilinder losmaken, brengen we de cilinder eerst naar een andere, warmere kamer. Als we nu in deze tweede kamer de zuiger loslaten en meten wat de maximale arbeid is die de cilinder kan verrichten, zal de uitkomst ons misschien meer verbazen. De energie die nu als arbeid geleverd kan worden, blijkt aanmerkelijk kleiner te zijn dan de hoeveelheid energie die we oorspronkelijk als warmte aan de cilinder hebben toegevoegd!

De verklaring voor dit verschijnsel is de volgende. Als het gas uitzet, zal het in evenwicht willen komen met de lucht buiten de cilinder – dan is immers zoals we gezien hebben de entropie van het totale systeem het hoogst. In dit geval betekent “in evenwicht” dat het gas in de cilinder en de lucht erbuiten dezelfde druk en temperatuur bereiken.

Doordat het gas in de cilinder uitzet, koelt het ook af. (Het omgekeerde hiervan is een bekend verschijnsel: wie een fietsband heeft opgepompt, kan aan de onderkant van de fietspomp goed voelen dat de gecomprimeerde lucht de pomp flink heeft opgewarmd.) In de warmere kamer zal het gas minder in temperatuur hoeven te dalen dan in de koudere kamer, en dus ook minder uitzetten. Dit is de reden dat de zuiger in de warmere kamer minder arbeid kan verrichten dan in de koudere kamer.

Afbeelding 2. De eerste definitie van entropieDe passage in het boek “The mechanical theory of heat” (1867) waarin Rudolf Clausius het thermodynamische begrip entropie definieert.

Een opmerking voor de perfectionisten: de situatie in de twee kamers hangt natuurlijk niet alleen af van de temperatuur, maar bijvoorbeeld ook van de luchtdruk in de twee kamers. We zijn er in het bovenstaande voor het gemak van uitgegaan dat de dichtheid van de lucht – dus het aantal atomen per liter – in de twee kamers hetzelfde is. Een betrekkelijk eenvoudige formule laat dan zien dat de luchtdruk in de warmere kamer ook hoger zal zijn dan die in de koudere kamer. Dit is een tweede manier om te begrijpen waarom het gas in de warmere kamer minder ver uitzet: het gas in de cilinder zal uitzetten tot de afnemende gasdruk gelijk is aan de luchtdruk in de kamer. In de warmere kamer hoeft het gas daarvoor dus minder ver uit te zetten.

We lijken nu op een tegenspraak gestuit te zijn, want hoe is het voorgaande in overeenstemming te brengen met de Eerste Hoofdwet, de wet van behoud van energie? We hebben meer energie als warmte aan de cilinder toegevoegd, dan we er als arbeid uit hebben gekregen – waar is het verschil gebleven? De oplossing van deze puzzel zit hem in het feit dat we niet alle soorten van energie hebben meegeteld. De atomen in het gas in de cilinder bewegen, en hebben daarmee zelf ook energie. In een warmer gas bewegen de atomen sneller, dus een warmer gas heeft meer inwendige energie dan een koud gas. Het gas in de cilinder zal in de warmere kamer dus meer inwendige energie hebben dan in de koudere kamer, en dit verschil in energie verklaart precies de “verloren” energie hierboven.

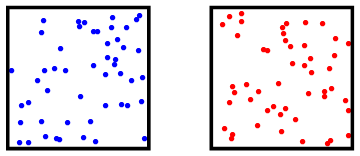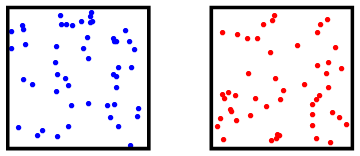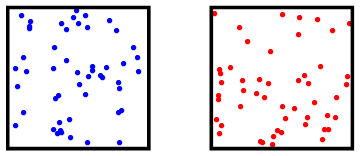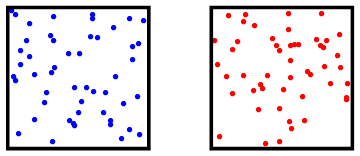
Afbeelding 3. Koud en warm gasIn een warm gas bewegen de atomen sneller dan in een koud gas; het warme gas heeft daarmee dus meer inwendige energie. Het gas rechts heeft een temperatuur die ongeveer zesmaal zo hoog is (gemeten in Kelvin) als het gas links.

Halverwege de 19e eeuw wist men, bij gebrek aan een volledige atoomtheorie, nog niet precies waar de inwendige energie van een gas uit bestond, maar het bovenstaande verschijnsel was wel duidelijk. Het werd als volgt geformuleerd: een systeem zoals een gas heeft energie in twee vormen: energie die omgezet kan worden in arbeid, en energie die niet omgezet kan worden. Het was bovendien duidelijk dat de energie die wel kan worden omgezet in arbeid, toeneemt naarmate de temperatuur van het systeem ten opzichte van de omgeving toeneemt. Als die relatieve temperatuur tweemaal zo hoog wordt gemaakt, kan het systeem ook twee keer zoveel arbeid leveren. De verhouding tussen “beschikbare energie” en “temperatuur ten opzichte van de omgeving” is dus constant, en deze constante werd de entropie genoemd.

Het moge uit onze beschrijving duidelijk zijn dat deze klassieke, thermodynamische definitie van entropie heel veel te maken heeft met de statistische vorm van entropie die we tot nu toe behandeld hebben. Sterker nog: toen de atoomtheorie eenmaal volledig ontwikkeld was, werd duidelijk dat de twee definities in feite dezelfde grootheid beschrijven. De eenheden waarin de twee gemeten werden was wel iets anders – net zoals het universele begrip “afstand” door bijvoorbeeld de Amerikanen in mijlen word gemeten, en door de meeste Europeanen in kilometers. Om een afstand in mijlen om te zetten in een afstand in kilometers, vermenigvuldigen we die met ongeveer 1,6. Op precies dezelfde manier kunnen we een “statistische entropie” omzetten in een “thermodynamische entropie” door die te vermenigvuldigen met een constant getal. Dat getal wordt de constante van Boltzmann genoemd; als we de vrijgekomen energie meten in Joules (J) en de temperatuur in Kelvin (K, graden Celsius ten opzichte van het absolute nulpunt) is die constante ongeveer 1,38 x 10^-23 J/K.

Dit is het vijfde artikel in het dossier Entropie. In het zesde artikel in dit dossier bespreken we wat entropie en de richting van de tijd met elkaar te maken hebben.

Afbeeldingsverantwoording: de afbeelding in het blokkenschema is afkomstig van Wikipedia.