Entropie (3): Van micro naar macro

Waarom loopt een gasfles leeg?

Atomen in een gas blijven niet op dezelfde plaats stilstaan. Ze vliegen met een bepaalde snelheid door de verder lege ruimte, botsen met de wanden van het compartiment en met elkaar, en bewegen zo kriskras door elkaar heen. We kunnen dat gedrag simuleren door de ballenbak te “schudden”. We verwisselen daarbij steeds twee willekeurige naast elkaar gelegen ballen in hetzelfde compartiment. Laten we aannemen dat er ook een kleine opening tussen de twee compartimenten is. Ook ballen die zich links en rechts van de opening bevinden kunnen op deze manier verwisseld worden.

In afbeelding 1 zien we een animatie van wat er nu gebeurt. De opening tussen de twee compartimenten is in het geel aangegeven. De totale animatie bestaat uit 600.000 verwisselingen, in een ballenbak met 800 ballen waarvan 20 rode. Aan het begin van de animatie zijn de rode ballen willekeurig over de rechterhelft van de bak verdeeld. In het compartiment rechts is dus een grote hoeveelheid “gas”; links is nog een vacuüm zonder gasatomen.

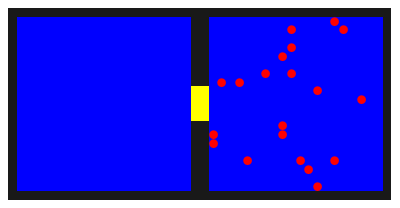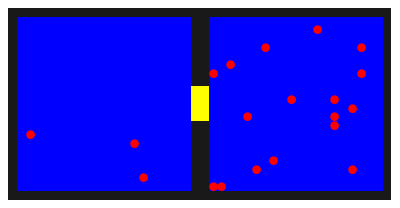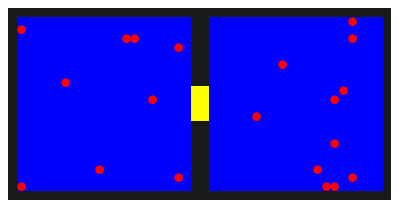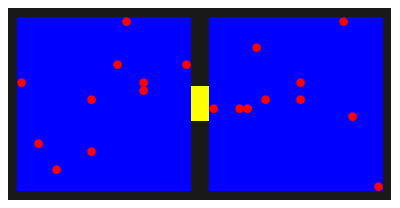
Afbeelding 1. Animatie van een leegstromende gasflesDe rode gasatomen bewegen zich willekeurig door de twee compartimenten, en kunnen via de gele opening van het ene naar het andere compartiment bewegen. Na enige tijd zijn de atomen evenwichtig verdeeld over de twee helften.

Op een gegeven moment komt een van de rode ballen terecht aan de rechterkant van de opening, en bestaat er een kans dat die bal verwisseld wordt met de blauwe bal links van de opening. Zodra dat gebeurt, is er dus één gasatoom in de linkerhelft van de bak, en zijn er nog 19 in de rechterhelft. Weer iets later kan zo nog een gasatoom “ontsnappen”, en wordt de verhouding 2:18. Natuurlijk kunnen ballen ook weer terug bewegen van links naar rechts. In de animatie gaat bijvoorbeeld de verhouding op een gegeven moment van 3:17 naar 2:18, als een van de drie ontsnapte gasatomen weer terug de rechterhelft in beweegt.

Op deze manier worden de ballen in de loop van de tijd flink door elkaar gehusseld, en zo zal uiteindelijk een situatie ontstaan waarin de ballen willekeurig over de twee helften verdeeld zijn. We weten uit het voorafgaande dat de kans enorm groot is dat die verdeling erg gelijkmatig is. In de animatie is de verdeling in het laatste frame bijvoorbeeld 11:9.

Merk op dat hier geen enkele “kracht” aan het werk is. Het is niet zo dat de atomen in de rechterhelft “elkaar naar buiten duwen” waardoor uiteindelijk een groot aantal atomen links terechtkomt. De atomen hebben geen enkele interactie met elkaar. Toch krijgen we een eindsituatie waarin de gasatomen gelijkmatig over de twee compartimenten verdeeld zijn.

De uiteindelijke gelijkmatige verdeling van de ballen is puur een statistisch effect. Zoals we in het vorige hoofdstuk zagen, is de kans op een gelijkmatige willekeurige verdeling vele malen groter dan de kans op een verdeling met alle ballen aan één kant van de bak. Het is niet onmogelijk dat de rode ballen uiteindelijk allemaal weer aan één kant van de bak terechtkomen; de kans daarop is alleen extreem klein.

Dit is de reden dat een gasfles leegloopt als we die opendraaien. Dat gebeurt niet omdat een onzichtbare kracht de gasatomen uit de fles naar buiten duwt, maar omdat we beginnen vanuit een enorm ongelijkmatige situatie: een situatie met alle atomen in de gasfles, en geen enkel gasatoom daarbuiten. De kans dat een gasatoom de fles uit vliegt, is dus als we de kraan nog maar net open hebben staan veel groter dan de kans dat een gasatoom de fles in vliegt. Pas als de fles “leeg” is (preciezer: als de dichtheid van gasatomen in de fles even groot is als de dichtheid van gasatomen daarbuiten) zijn die twee kansen ongeveer gelijk, en ontstaat een evenwichtssituatie waarbij grofweg evenveel atomen de fles in als uit zullen bewegen.

Theoretisch bestaat daarbij altijd de kans dat alle atomen de fles weer in vliegen, maar die kans is zo onnoemelijk klein dat we die in de praktijk kunnen verwaarlozen. In het bovenstaande voorbeeld is die kans aan het eind van de animatie zo’n 0,0001%. In een realistische gasfles zitten niet 20 gasatomen, maar een aantal dat zelf een getal van meer dan 20 cijfers is. De kans dat ál die atomen toevallig weer de gasfles in bewegen, is dusdanig klein dat we die op geen enkele praktische manier meer van 0 kunnen onderscheiden.

Microscopische en macroscopische toestanden

Laten we nog eens teruggaan naar een eerder gemaakte  opmerking: de kans op elke specifieke verdeling van ballen in onze ballenbak is precies gelijk. Wanneer we de ballen willekeurig over de compartimenten verdelen, hebben de drie verdelingen in de afbeeldingen 2, 3 en 4 dus alle drie dezelfde kans om te ontstaan. We zeggen dat de afbeeldingen 2, 3 en 4 alle drie een even waarschijnlijke microscopische toestand weergeven.

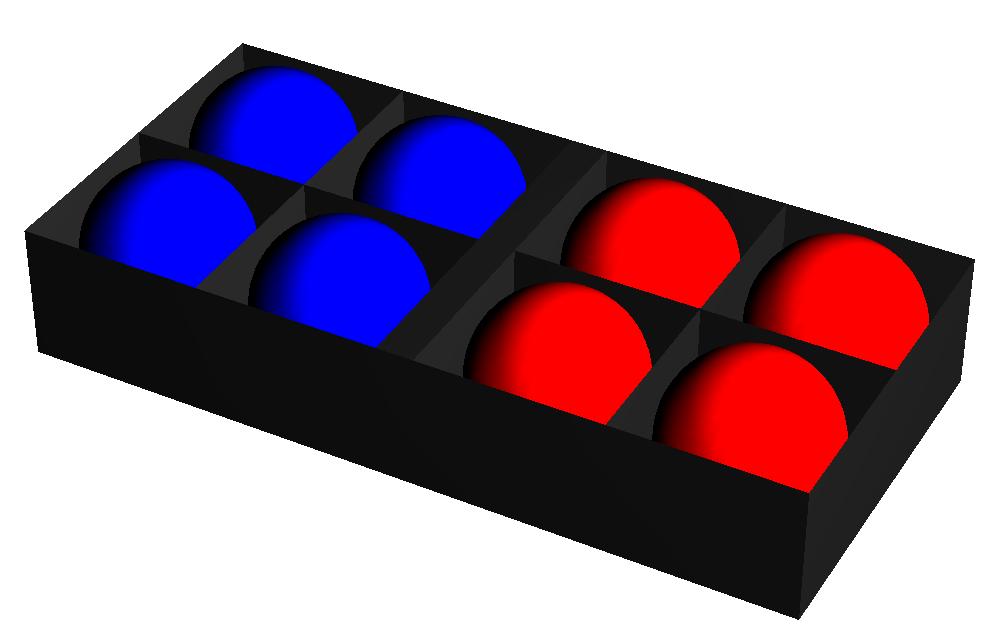
Afbeelding 2. Ballenbak (gesorteerd)

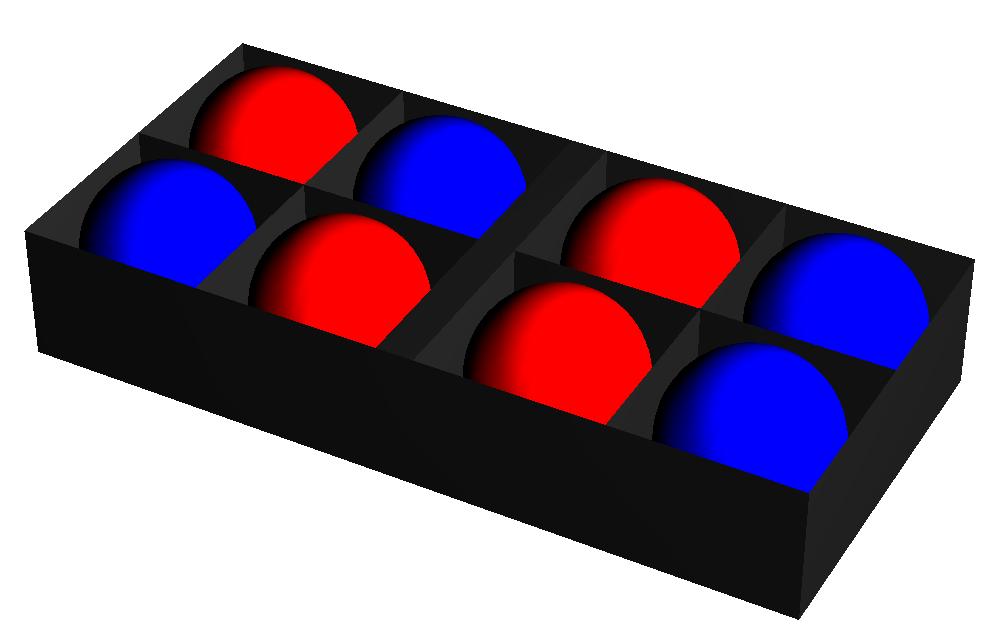
Afbeelding 3. Ballenbak (ongesorteerd)

Afbeelding 4. Ballenbak (ongesorteerd)

Afbeelding 3 en 4 dragen echter allebei bij aan de “gelijkmatige” situatie, met twee ballen aan elke kant. Dat wil zeggen: in ons experiment waren we niet geïnteresseerd in de precieze posities van alle ballen, maar alleen in het aantal rode en blauwe ballen aan elke kant. Afbeelding 2 draagt dus (als enige) bij aan de macroscopische toestand “0:4”, en afbeelding 3 en 4 (en nog 34 soortgelijke afbeeldingen) dragen bij aan de macroscopische toestand “2:2”.

In zekere zin ontstaan de grote verschillen in waarschijnlijkheid dus doordat we informatie hebben “weggegooid”: wanneer we alleen weten dat de ballenbak in de macroscopische toestand “2:2” is, weten we niet precies hoe de ballen verdeeld zijn – die ene macroscopische toestand beschrijft 36 verschillende microscopische toestanden. Op dezelfde manier beschrijft de macroscopische toestand “1:3” zestien verschillende microscopische toestanden (zie afbeelding 5), en komt de macroscopische toestand “4:0” overeen met één enkele microscopische toestand.

In ons voorbeeld is het weggooien van informatie een vrijwillige keuze geweest – we kunnen de toestanden van de ballenbak ook zonder veel problemen op microscopisch niveau beschrijven. In veel natuurkundige systemen is het echter praktisch onmogelijk om  de microscopische toestand van het systeem te beschrijven. Denk bijvoorbeeld weer aan het gas in een gasfles. Dit gas heeft diverse macroscopische eigenschappen die we eenvoudig kunnen meten, zoals de temperatuur van het gas, de druk die het gas uitoefent op de wanden van de gasfles, of het volume dat het gas inneemt.

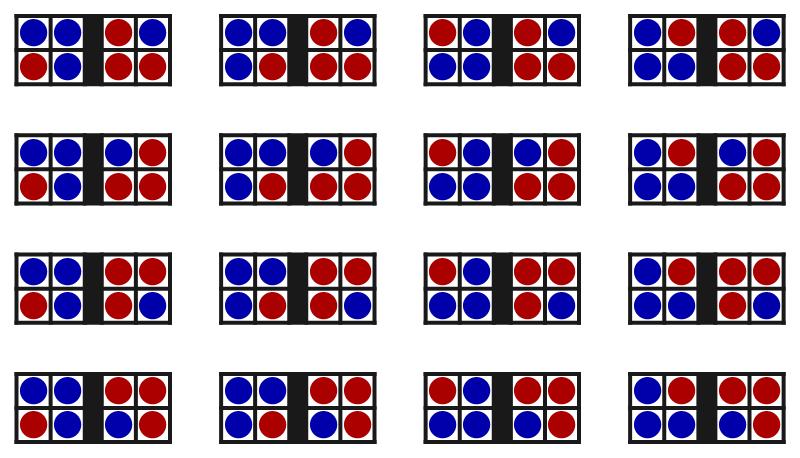
Afbeelding 5. De configuraties van de ballenbakDe zestien microscopische toestanden die overeenkomen met de macroscopische toestand “1:3”.

Het meten van de precieze microscopische toestand van het gas is echter vrijwel onmogelijk. Daarvoor zouden we van elk atoom in het gas moeten bepalen op welke plaats het zich precies bevindt, en met welke snelheid het in welke richting beweegt. In een realistisch gas is het aantal atomen zoals gezegd een getal van meer dan 20 cijfers, dus het moge duidelijk zijn dat dit in de praktijk volkomen ondoenlijk is. En dat niet alleen: zelfs als we een dergelijke meting zouden kunnen doen, zou de enorme hoeveelheid informatie ons nauwelijks meer vertellen over de eigenschappen van het gas dan we al wisten. Alle interessante kenmerken van het gas hangen alleen af van de temperatuur, de druk en het volume, en niet van de precieze configuratie van atomen die tot die grootheden leidt. De microscopische toestand van het gas is in onze macroscopische wereld dus niet alleen onmeetbaar, maar ook oninteressant.

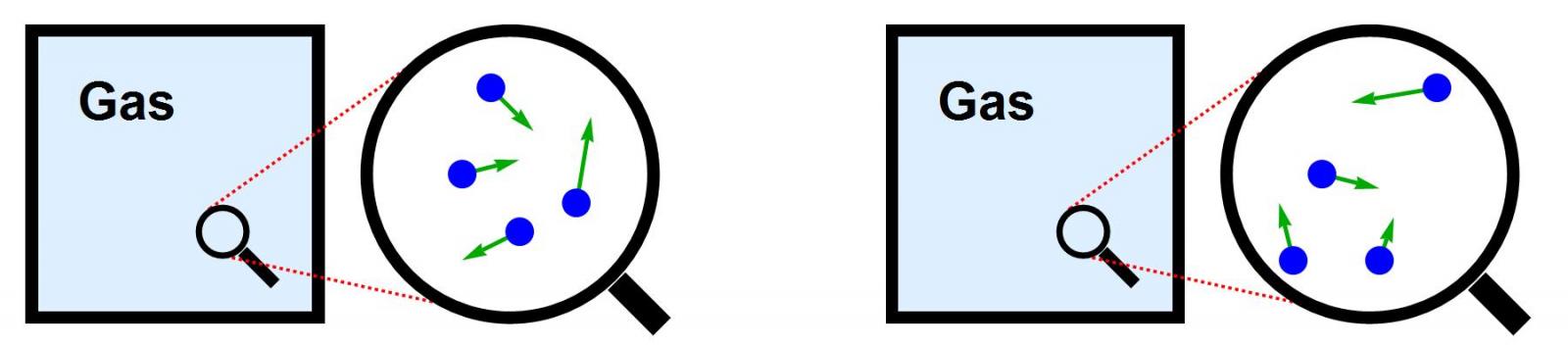
Afbeelding 6. Een gas.Eén macroscopische toestand komt overeen met enorm veel microscopische toestanden. De microscopische parameters, zoals de posities en snelheden van individuele atomen, zijn in het algemeen onmeetbaar en oninteressant.

Het weggooien van de microscopische informatie heeft dus in de macroscopische praktijk weinig merkbaar effect. Het enige wat we moeten onthouden is dat, net als in het voorbeeld van de ballenbak, niet elke macroscopische toestand overeenkomt met evenveel microscopische toestanden. In het algemeen zullen, zoals we gezien hebben, macroscopische toestanden met een gelijkmatig karakter extreem veel waarschijnlijker zijn dan macroscopische toestanden met een ongelijkmatig karakter. In het voorbeeld van de gasfles betekent dat dat na verloop van tijd de gasdruk en -dichtheid binnen en buiten de fles precies gelijk zullen zijn: de fles loopt leeg. In het geval van een kop thee betekent het dat na verloop van tijd de temperatuur binnen en buiten de kop gelijk zullen zijn: de thee koelt af. In theorie is het niet uitgesloten dat de gasfles spontaan weer volstroomt of dat de thee spontaan weer opwarmt, maar die kans is zo extreem klein dat we zoiets in een mensenleven (en zelfs: gedurende de leeftijd van het heelal) niet zullen meemaken.

Dit is het derde artikel in het dossier Entropie. In het vierde artikel in dit dossier wordt het begrip entropie heel precies gedefinieerd, en maken we kennis met de Tweede Hoofdwet van de thermodynamica, die zegt dat entropie nooit afneemt.

Afbeeldingsverantwoording: de afbeelding van de gasbrander in het blokkenoverzicht komt van deze website