Zwemmen op microschaal (1)

Afbeelding 1. Een E. colibacterie.Een E. coli-bacterie is van micrometergrootte en kan zwemmen door een bundel van lange flagella achter zich rond te draaien. Bron: BioCote.

Navier, Stokes en Reynolds

Zoals we eerder in deze serie hebben gezien, worden vloeistofstromen beschreven door de Navier-Stokesvergelijkingen. In hun volle glorie zien die er als volgt uit:

De precieze details van deze vergelijking zijn niet van belang, maar de ingrediënten wel. Zo zijn ρ, u en p respectievelijk de massadichtheid, de snelheid en de druk van een vloeistofelement.

De materiaalconstante η is de viscositeit. Hoewel de Navier-Stokesvergelijking een zeer moelijke vergelijking is, beschrijft die eigenlijk iets eenvoudigs: een krachtenbalans die volgt uit de 2^e wet van Newton, waarbij de traagheid van een vloeistofelement (links) gebalanceerd wordt met de wrijvingskrachten op het vloeistofelement (rechts). Wanneer we onderzoeken hoe deze effecten schalen met de typische eigenschappen van het systeem dat we beschrijven, vinden we dat de traagheid als functie van die eigenschappen schaalt als ~ ρV²/L, terwijl de wrijving schaalt als ~ ηV/L², waarbij V en L de typische snelheid en grootte van ons systeem zijn. Wanneer we deze schalingen door elkaar delen, dan vinden we een getal dat de grootte van de traagheid en die van de wrijving vergelijkt, het Reynoldsgetal:

Wanneer dit Reynoldsgetal groot is, zijn traagheidseffecten dus belangrijk. Deze situatie leidt tot chaotische stromen. Aan de andere kant: wanneer het Reynoldsgetal (heel) klein is, is wrijving veel belangrijker dan traagheid, en kunnen we de traagheid dus verwaarlozen, wat soms tot bizarre effecten kan leiden – zoals te zien is in het filmpje in artikel 3 van deze serie.

Wanneer is dit Reynoldsgetal klein? Als we vergelijking (2) bekijken, zien we dat het Reynoldsgetal bijvoorbeeld klein is wanneer de typische snelheid van de vloeistof (V) klein is, of wanneer het systeem dat we beschrijven zelf klein is (L klein), of wanneer de vloeistof heel stoperig is (η groot). Met andere woorden: hydrodynamica van water op heel kleine schaal is hetzelfde als hydrodynamica van stroop op grote schaal!

Zwemmen met Reynoldsgetallen

Om dit alles verder te onderzoeken, moeten we wat typische getallen invullen. Mensen zwemmen meestal in water, wat een dichtheid heeft van ρ ~ 10³ kg/m³ en een viscositeit van η ~ 10^-3 Pa s. Voor het gemak zeggen we dat mensen ongeveer een meter groot zijn (L ~ 1 m) en zwemmen met een snelheid die ook van die orde van grootte is (V ~ 1 m/s).

Als we dit invullen in vergelijking (2), vinden we dat het Reynoldsgetal ongeveer 10⁶ is, dus traagheid – het feit dat een beweging moeilijk afgeremd of versneld wordt – is voor mensen die in het water zwemmen erg belangrijk. Dit zien we bijvoorbeeld bij een zwemwedstrijd, waarbij de goede zwemmers vele meters onder water doorglijden nadat ze van het startblok in het water duiken.

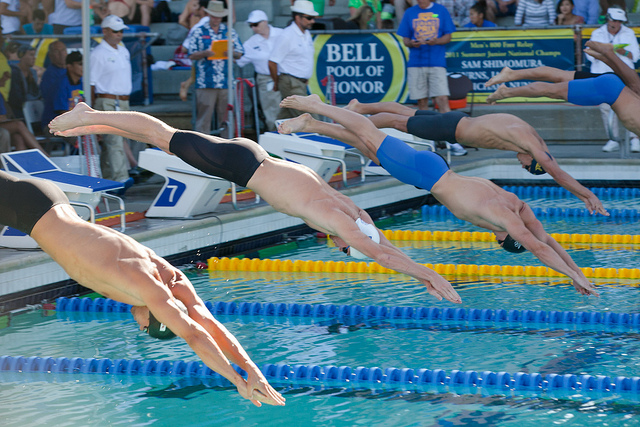
Afbeelding 2. De start van een zwemwedstrijd.Nadat de zwemmers in het water terechtkomen, komen ze niet direct tot stilstand, maar glijden ze nog een groot stuk onder water door. Met andere woorden: er is een grote traagheid. Foto: JD Lasica.

Maar stel nu dat we het zwemmen van een bacterie willen beschrijven. Een typische bacterie is ongeveer een micrometer groot (L ~ 1 μm) en zwemt met een snelheid V ~ 10 μm/s, zodat vergelijking (2) nu een Reynoldsgetal van ongeveer 10^-4 oplevert. Voor bacteriën is wrijving dus veel belangrijker dan traagheid.

Om dit verschil nog wat duidelijker te maken, kunnen we kijken naar de stopafstand in beide voorbeelden: we stellen ons voor dat een mensen en een bacterie van het startblok in het zwembad duiken en we maken een schatting van de afstand waarna ze tot stilstand komen. We nemen voor het gemak aan dat de massadichtheid van de zwemmer vergelijkbaar is met die van de vloeistof, zodat onze zwemmer (met grootte L)  ongeveer een volume L³ en een massa ρL³ heeft. Zoals hierboven beschreven, geldt dat de inertiële krachtdichtheid (de traagheid) schaalt als ρV²/L, terwijl de viskeuze krachtdichtheid (de wrijving) schaalt als ηV/L². We vermenigvuldigen deze krachtdichtheden met het volume L³ om de krachten zelf te vinden, gebruiken vervolgens de 2^e wet van Newton (kracht is massa keer versnelling), en vinden zo dat de traagheid leidt tot een vertraging a ~ V²/L als gevolg van de traagheidseffecten en a ~ ηV/(ρL²) als gevolg van de wrijving.

Aan de hand van de vertraging kunnen we ten slotte een remweg s = V²/(2a) uitrekenen na welke de zwemmer tot stilstand komt. De enthousiaste lezer die alle sommetjes zelf doet, zal tot de volgende conclusie komen. Voor een hoog Reynoldsgetal (de traagheid domineert) volgt dat s ~ L, dus wij mensen glijden nog een paar meter door het water wanneer we in het zwembad duiken. Voor een laag Reynoldsgetal (de wrijving domineert) geldt daarentegen dat s ~ L × Re, zodat een bacterie na een afstand van ongeveer 1 Å (10^-10 m) tot stilstand komt wanneer die stopt met zwemmen – vele malen minder dan zijn eigen lengte! Voor een bacterie lijkt het water waar die doorheen probeert te zwemmen dus enorm stroperig: wanneer wij mensen in een situatie met hetzelfde Reynoldsgetal zouden zwemmen als een bacterie, zouden we al na s ~ L × Re ≈ 0.1 mm tot stilstand komen! Zo beschouwd is het alsof een bacterie door een muur moet zwemmen. Het is dus best indrukwekkend dat er überhaupt bacteriën zijn die vooruit komen op die kleine schaal.

Stroperigheid van vloeistoffen op kleine schaal maakt het dus moeilijk om vooruit te komen. Daarnaast heeft het ontbreken van traagheid op microschaal echter nog meer gevolgen voor zwemmen op kleine schaal. Wat die gevolgen zijn, en wat ze te maken hebben met zwemmende schelpen, beschrijven we in een volgend artikel dat over enkele weken op deze site verschijnt.