
Zwarte gaten
Zwarte gaten zijn verwarrende en daardoor fascinerende objecten, en dat is al ruim honderd jaar zo, sinds Karl Schwarzschild in 1916 de eerste bolsymmetrische oplossing van de net ontdekte Einsteinvergelijkingen vond. Deze Schwarzschildoplossing is een van de meest dramatische voorspellingen van Einsteins algemene relativiteitstheorie: de oplossing voorspelt dat er objecten bestaan die zo’n sterke zwaartekracht hebben dat niets, zelfs niet het licht, aan ze kan ontsnappen zodra het voorbij een zogeheten horizon rondom dit object komt. We kunnen iemand met enig gevoel voor drama, de Amerikaanse natuurkundige John Wheeler, bedanken voor de naam ‘zwart gat’.
Zwarte gaten worden door verschillende groepen mensen om totaal verschillende redenen interessant gevonden. Zo is de onomkeerbaarheid van het vallen door de horizon, en het mysterie van wat er gebeurt bij de singulariteit in het midden van het zwarte gat, een uitstekende reden om ze te verwerken in sciencefictionverhalen, zoals Interstellar. Daarnaast zijn zwarte gaten voor sterrenkundigen aanleiding tot enorme internationale samenwerkingsverbanden zoals de Event Horizon Telescope (EHT), waaraan meer dan 300 mensen, 60 instituten en 20 landen deelnemen. Hierbij wordt een grote reeks radiotelescopen verspreid over de aarde zo gecoördineerd dat ze als het ware één grote telescoop ter grootte van de aardbol vormen. Deze telescoop slaagde er in 2019 in de eerste foto van een zwart gat te schieten, namelijk dat in het centrum van het sterrenstelsel Messier 87. In 2022 volgde een foto van het zwarte gat Sagittarius A*, in het centrum van ons eigen sterrenstelsel.
Nog een voorbeeld van dergelijke samenwerkingsverbanden zijn telescopen als LIGO (VS) en VIRGO (Italië). Dit zijn geen telescopen zoals je je misschien voorstelt, maar interferometers. Deze interferometers zijn gebouwd om zwaartekrachtsgolven te meten, nog een van de meest dramatische voorspellingen van de algemene relativiteitstheorie. Een interferometer bestaat uit twee laserbundels die in een rechte hoek ten opzichte van elkaar weggeschoten worden, en teruggekaatst worden door spiegels, waarna de laserbundels weer recombineren bij het beginpunt. Laserbundels zijn lichtgolven, en wanneer ze recombineren vindt er interferentie plaats: als de golf van de ene laserbundel zich in een dal bevindt en de golf van de andere laserbundel in een piek, dan heffen ze elkaar op. Als de golven zich op hetzelfde punt in hun cyclus bevinden bij recombinatie, dan versterken ze elkaar. Dit principe wordt gebruikt om extreem precies de lengte van de twee tunnels waarin de lasers heen en weer bewegen te meten: met een precisie vergelijkbaar met het meten van de afstand tussen Amsterdam en New York met een nauwkeurigheid ter grootte van de dikte van een haar. Als er in de meetopstelling een zwaartekrachtsgolf voorbij komt, bijvoorbeeld veroorzaakt door twee zwarte gaten die heel snel om elkaar heen cirkelen voordat ze elkaar opslokken en daarbij letterlijk een golf in de kromming van de ruimte veroorzaken, dan veranderen de tunnels van lengte. Dit is maar een extreem klein effect, en dit is de reden dat de tunnels meerdere kilometers lang zijn en dat hun lengte extreem precies gemeten moet worden. Zeer recent, in 2016, begonnen deze telescopen zwaartekrachtsgolven te detecteren, bij de eerste meting inderdaad veroorzaakt door de samensmelting van twee zwarte gaten met beide een massa van grofweg 30 zonnen, hier 1,3 miljard lichtjaar vandaan.
Quantummechanische zwarte gaten: entropie
De genoemde verschijnselen zijn klassieke, dat wil zeggen: niet quantummechanische, aspecten van zwarte gaten die bestudeerd worden. Wat Stephen Hawking echter in 1974 ontdekte, is dat de quantumvelden rondom de horizon van een zwart gat ervoor zorgen dat het zwarte gat straalt, waardoor het energie verliest en dus langzaam verdampt. Dit gaat in tegen wat we van klassieke zwarte gaten weten, namelijk dat alles wat voorbij de horizon van een zwart gat valt, er niet meer uit kan. Het zwarte gat kan dus alleen maar groter worden, en niet kleiner. Daarnaast impliceert het feit dat het zwarte gat straalt dat het een temperatuur heeft, wat thermodynamisch betekent dat het ook een entropie heeft. Gek genoeg is deze entropie evenredig met de grootte van het oppervlak van de horizon van het zwarte gat. In een formule:
\( S_{BH} = \frac{A_{hor}}{4G} \),
waarin \( S_{BH} \) de entropie is, \( A_{hor} \) de grootte van het oppervlak, en \( G \) de zwaartekrachtconstante van Newton. Het schalen met het oppervlak is vreemd, omdat de entropie van een systeem gewoonlijk schaalt met het volume van dat systeem. De formule hierboven is de Bekenstein-Hawkingformule. Dat entropieën evenredig zijn met oppervlakten in de ruimtetijd zullen we meer zien. De Bekenstein-Hawkingformule is namelijk een eerste voorbeeld van wat later door Leonard Susskind en Gerard ’t Hooft het holografische principe werd genoemd: holografisch omdat de informatie in het zwarte gat gecodeerd wordt op het oppervlak van het systeem, net als bij een ‘echt’ hologram.
Als we de entropie van een gebied in de ruimtetijd willen weten, en er is een zwart gat in dat gebied, dan moeten we dus niet alleen de entropie van materie, of quantumvelden, meenemen, maar ook de Bekenstein-Hawking entropie. Samen vormen die wat we gegeneraliseerde entropie \(S_{gen}\) noemen:
\( S_{gen} = S_{BH} + S_{mat} = \frac{A_{hor}}{4G} + S_{mat}\).
Een bijkomend voordeel is dat de gegeneraliseerde entropie de tweede hoofdwet van de thermodynamica niet overtreedt: deze entropie kan alleen maar toenemen.
De informatieparadox
Het gegeven dat zwarte gaten stralen, leidt uiteindelijk zelfs tot een beroemde paradox: de informatieparadox. Eén enigszins gepopulariseerde manier om die paradox te formuleren is dat objecten die in een zwart gat vallen een bepaalde hoeveelheid informatie bevatten, denk aan dit artikel op een USB stick. Als het zwarte gat vervolgens verdampt en verdwijnt, wat is er dan met die informatie gebeurd? Een fundamentele wet van de quantummechanica zegt dat die informatie niet verloren mag zijn gegaan. Dit was dan ook de inzet van een beroemde weddenschap in 1997 tussen Stephen Hawking en Kip Thorne, die dachten dat zwarte gaten informatie vernietigen, en John Preskill, die geloofde in de wetten van de quantummechanica.

Het behoud van informatie staat in de quantummechanica bekend als het principe van unitariteit van tijdsevolutie: het moet mogelijk zijn om, gegeven een bepaalde toestand van het universum, terug te redeneren hoe het universum er een bepaalde tijd eerder uitzag – en andersom. Alle informatie over hoe het universum er in het verleden uitzag, zou volgens de quantumwetten dus in de huidige toestand van het universum teruggevonden moeten kunnen worden. De informatie die in een zwart gat is gevallen, lijkt in Hawkings analyse bovendien niet te ontsnappen door de straling. Het zwarte gat is namelijk bij goede benadering een zwarte straler, wat betekent dat alle aspecten van de straling die het uitzendt alleen bepaald worden door de temperatuur van het zwarte gat, die op haar beurt weer bepaald wordt door de massa van het zwarte gat. Als ik dus twee zwarte gaten onderzoek die allebei even zwaar zijn, en ik gooi in één zwart gat een exemplaar van The Origin of Species van Charles Darwin, en in het andere zwarte gat een exemplaar van de Bijbel, dan zijn, aangenomen dat de twee boeken even zwaar zijn, de eindresultaten na verdamping niet van elkaar te onderscheiden. De vrijgekomen straling is immers alleen van de massa afhankelijk. Dit terwijl de twee boeken toch totaal verschillende informatie bevatten – die informatie gaat dus verloren.
Quantumzwaartekracht
We zijn in het bovenstaande verhaal nog ver verwijderd van enig verschijnsel dat praktisch gezien te meten valt. De straling die een zwart gat uitzendt heeft slechts een temperatuur van ongeveer een honderd miljoenste graad boven het absolute nulpunt (ongeveer -273 graden Celsius), aangenomen dat het zwarte gat grofweg de massa van onze zon heeft (zoals de kleinste zwarte gaten die we kennen). Zelfs vlakbij zo’n zwart gat zou het lastig zijn die straling te detecteren. Om een serieus experiment te doen zou je ook een significant deel van de straling op moeten vangen die een zwart gat uitstraalt, maar een zwart gat met de massa van de zon doet er 1063 jaar over om volledig te verdampen. Doordat een zwart gat maar een heel klein beetje straling uitzendt, verdampt het namelijk ook extreem langzaam. Dit zou enige zorgen moeten baren: de wetenschap is immers een empirische bezigheid. Ook gedachte-experimenten over onrealistische situaties zijn echter vaak een belangrijke stap in de wetenschap gebleken. Denk aan Einstein, die nadacht over treinen die bijna met de snelheid met het licht reizen om zo de speciale relativiteitstheorie te ontdekken.
In het huidige geval hebben we twee theorieën, de quantumveldentheorie en de algemene relativiteitstheorie, die allebei afzonderlijk experimenteel extreem goed getest en geverifieerd zijn, maar wel in situaties waarin slechts één van de theorieën relevant is. Wanneer je echter situaties wil beschrijven waarin beide relevant zijn, zoals de verdamping van een zwart gat, blijkt het combineren van de theorieën vaak te leiden tot paradoxen en resultaten die nergens op slaan. Een prominent voorbeeld is de genoemde informatieparadox van zwarte gaten. Hoewel situaties als deze in de praktijk geen enkele relevantie hebben, is het begrijpen hoe deze paradoxen zichzelf oplossen en het vinden van een consistente theorie van enorm belang voor het begrip van hoe ons universum werkt op het meest fundamentele niveau. De hoop is dan ook dat, wanneer er een nieuwe consistente theorie wordt gevonden, dat leidt tot onvoorziene en testbare voorspellingen. Verwacht wordt dat het vinden van zo’n theorie een uitdaging zal zijn, gezien het enorme verschil in energieniveaus van de situaties waarin quantum- en relativistische effecten plaatsvinden, zeker als je dat afzet tegen de experimenteel bereikbare energieniveaus. Dit zien we al voor de meest veelbelovende oplossing van het quantumzwaartekrachtprobleem, de snaartheorie – het idee dat het universum op zijn meest fundamentele niveau van draadjes is gemaakt in plaats van van puntdeeltjes.
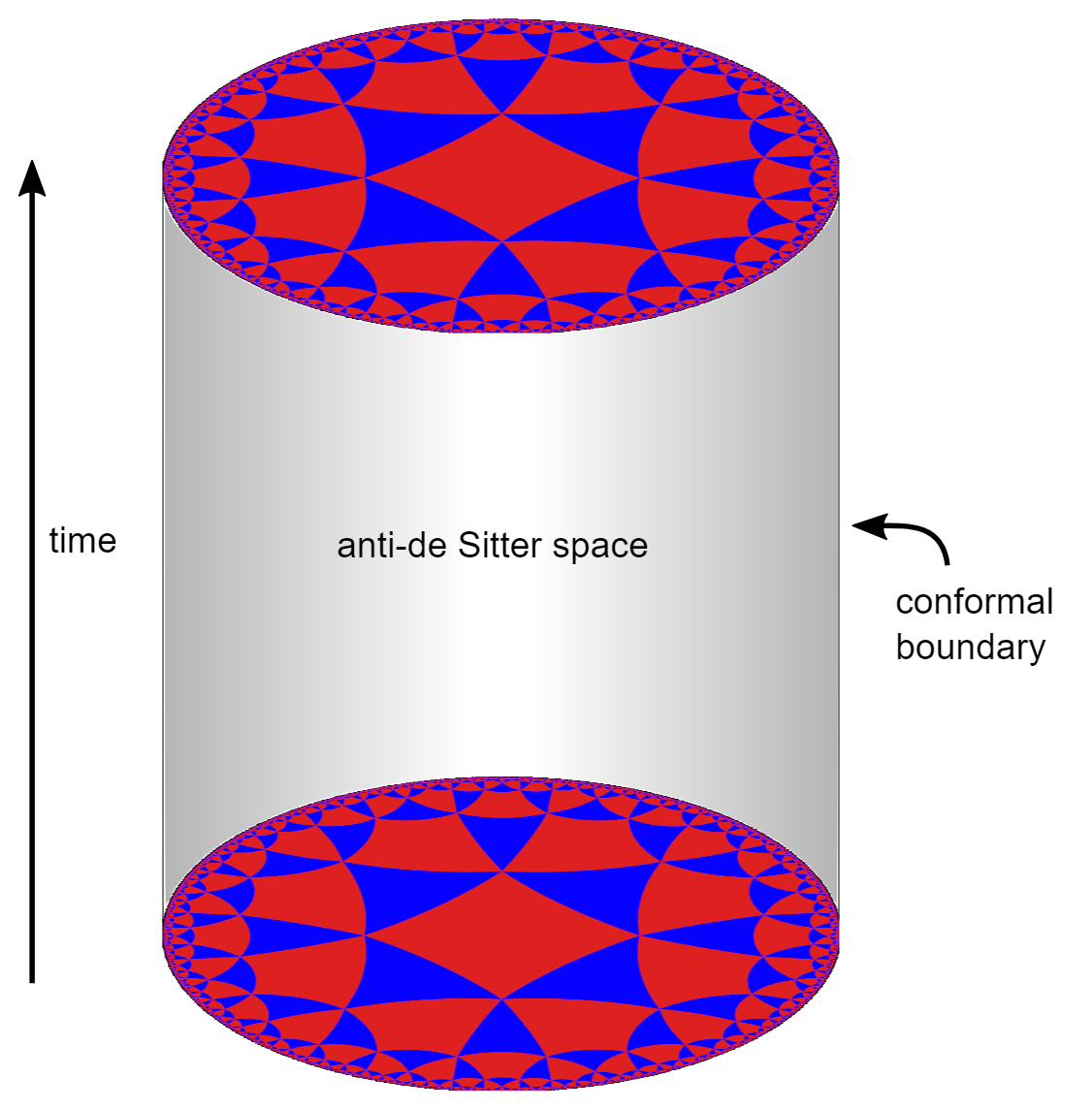
Uiteindelijk werd de weddenschap tussen Hawking en zijn collega’s beëindigd nadat Hawking in 2004 zijn ongelijk toegaf, een aantal jaar nadat Juan Maldacena met de eerste echte realisatie van het holografische principe kwam: de AdS/CFT-dualiteit. Die dualiteit zegt dat snaartheorie, een theorie met zwaartekracht dus, in een negatief gekromde ruimtetijd, Anti-de Sitter-ruimtetijd, en in bepaalde regimes, ook beschreven kan worden door een quantumveldentheorie (preciezer: een bijzondere subcategorie daarvan, conforme veldentheorie) in een ruimtetijd met één dimensie minder. Men zegt ook wel dat de duale quantumveldentheorie op de rand van de Anti- de Sitter ruimte leeft. Deze quantumveldentheorie houdt zich precies aan de wetten van de quantummechanica – de naam zegt het al – en dus kan net als in die theorie ook in de duale zwaartekrachtstheorie geen informatie vernietigd worden. Maldacena’s resultaat is als het ware een proof of concept. Het was genoeg om Hawking ervan te overtuigen dat zwarte gaten geen informatie vernietigen, maar het zegt nog niets over hóe die informatie dan na de verdamping uit het zwarte gat is ontsnapt.
Verstrengeling en de Page-kromme
Wat in ieder geval verwacht wordt een belangrijke rol te spelen in de oplossing van het quantumzwaartekrachtraadsel is verstrengeling, een fundamentele eigenschap van de quantummechanica. Om te begrijpen wat verstrengeling is moeten we om te beginnen weten wat een quantumtoestand is. Een elektron heeft bijvoorbeeld een eigenschap die spin heet. Het enige wat voor ons verhaal van belang is, is dat de spin van het elektron wanneer je die meet in twee toestanden kan verkeren: ‘spin up’ of ‘spin down’. Voordat je de spin van het elektron echter meet kan het elektron in allebei de toestanden tegelijk zijn: een zogenaamde superpositie. Een toestand waarin een elektron zich bijvoorbeeld voor 80 procent in een spin-uptoestand bevindt en voor 20 procent in een spin-downtoestand, betekent het volgende: wanneer je een groot aantal elektronen in precies die toestand prepareert, en je van allemaal de spin gaat meten, zul je in 20 procent van de gevallen spin down meten, en in 80 procent van de gevallen spin up. Belangrijk hierbij is dat het elektron vóórdat je meet niet in een van beide toestanden verkeert, en dat je alleen niet weet in welke. Met slimme interferentie-experimenten kun je dat aantonen: het elektron verkeert echt in een superpositie van beide toestanden. De kans op een bepaalde uitkomst is dus echt een fundamentele kans, en niet een kans die berust op onwetendheid. Belangrijk voor later: wiskundig gezien zijn deze quantumtoestanden deel van wat een Hilbertruimte heet. De spin up- of spin down-toestanden waarin het deeltje zich na een meting kan bevinden, labelen de dimensies van deze ruimte. In dit voorbeeld is de Hilbertruimte dus tweedimensionaal. De toestand van een het elektron is dan een pijltje, of vector, in deze ruimte, met lengte 1. Dat pijltje wijst meer in de richting van de ‘spin-updimensie’ als er meer kans is dat je spin up zult meten, en het wijst meer in de richting van de ‘spin-downdimensie’ als er meer kans is spin down te meten.
Een voorbeeld van verstrengeling vind je wanneer twee van zulke elektronen in een gecombineerde toestand verkeren, waarbij ik bijvoorbeeld met 80 procent kans spin up vind wanneer ik het ene elektron meet, maar zodra ik dat doe, de toestand van het andere elektron ook vastgelegd wordt, en er dan 100 procent zekerheid is dat iemand bijvoorbeeld spin down bij dat elektron zal meten. Van zulke verstrengeling kan zelfs sprake zijn wanneer de twee elektronen lichtjaren van elkaar verwijderd zijn – en toch is het vastleggen van de tweede spin na de meting aan de eerste iets wat instantaan gebeurt. Een maat voor de hoeveelheid verstrengeling van een deelsysteem met de rest van het systeem, is de von Neumann-verstrengelingsentropie. Kort door de bocht meet die grootheid hoeveel onzekerheid er met een bepaalde toestand geassocieerd kan worden, of anders gezegd: hoeveel informatie je potentieel kan verkrijgen over de rest van het systeem door een meting te doen aan het deelsysteem.
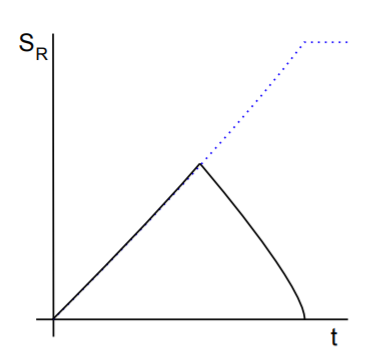
Om te begrijpen wat we verwachten dat er zal gebeuren bij een verdampend zwart gat, als er geen informatie verloren gaat, doen we het volgende gedachtenexperiment. Stel je voor dat we wat spullen, zeg een fiets, een bureaustoel en een boterham met pindakaas, bij elkaar proppen in een verder leeg universum. We proppen deze spullen zo sterk in elkaar dat er een zwart gat ontstaat. Zoals beschreven gaat dat zwarte gat straling uitzenden. Vervolgens ga ik alle straling die het zwarte gat uitstraalt opvangen, zodat ik precies weet wat er allemaal uit het zwarte gat is gekomen. Aan het begin is er veel onzekerheid over de informatie die in de straling zit die ik heb opgevangen. Er is namelijk nog geen manier voor mij om er op basis van de beperkte hoeveelheid straling achter te komen of die straling informatie over de fiets bevat, of over de boterham met pindakaas. De kennis die ik heb, maar ook de onzekerheid en daarmee de verstrengelingsentropie van de opgevangen straling, neemt zo dus toe. Wanneer het zwarte gat echter helemaal verdampt is en ik alle straling heb opgevangen, weet ik precies welke informatie ik heb, namelijk de informatie in de fiets, bureaustoel en het broodje pindakaas die het zwarte gat vormden. Er is geen onzekerheid meer: de verstrengelingsentropie is weer nul. Dit proces van omhoog- en omlaag gaan van de verstrengelingsentropie wordt de Page-kromme genoemd, vernoemd naar de natuurkundige Don Page. De Page-kromme is te zien in afbeelding 4. Het keerpunt in het proces wordt de Page-tijd genoemd; het is grofweg het moment halverwege het verdampingsproces van het zwarte gat. Daarnaast wordt in de afbeelding getoond wat er volgens Hawkings oorspronkelijke berekening, mét informatieverlies, zou moeten gebeuren: een constante stijging van de verstrengelingsentropie.
De Page-kromme reproduceren
In 2019 werd door onder andere de natuurkundige Geoff Penington een gedeeltelijk antwoord bedacht op de vraag hoe een zwart gat precies verdampt – een antwoord dat de gewilde Page-kromme reproduceert (zie ook de artikelen van oud-redactielid Evita Verheijden hier en hier). De oplossing van Penington en collega’s is gebaseerd op de gravitationele padintegraal. Een padintegraal is een manier om quantummechanica te beschrijven, waarbij er rekening wordt gehouden met het feit dat een deeltje dat van A naar B reist, quantummechanisch gezien alle mogelijke paden tussen die twee punten tegelijk neemt. Het eigenlijke ‘pad’ is een soort superpositie van al die paden, waarbij elk pad minder zwaar meegewogen wordt naarmate het afwijkt van het pad dat het deeltje klassiek gezien zou nemen. De gravitationele padintegraal volgt hetzelfde idee, toegepast op de zwaartekracht, ofwel de ruimtetijd. Die padintegraal sommeert over alle mogelijke vormen van de ruimtetijd, met wegingsfactoren die lichter wegen naarmate de ruimtetijd afwijkt van een klassieke oplossing van Einsteins vergelijkingen. Zo’n padintegraal zou een complete theorie van quantumzwaartekracht moeten produceren. Aangezien we echter niet zo goed weten wat al deze mogelijke ruimtetijden zijn, kunnen we niet veel beter doen dan alleen sommeren over heel kleine afwijkingen van de klassieke ruimtetijden. Dit noemen we een semi-klassieke benadering.
De semi-klassieke gravitationele padintegraal geeft een heel tegenintuïtief resultaat. Het resultaat wordt het voorschrift van het quantum-extremale oppervlak genoemd. Dat voorschrift zegt dat we de gegeneraliseerde entropie moeten berekenen op een oppervlak wat ‘quantum-extremaal’ is. Het idee vindt zijn oorsprong in het holografische principe wat we eerder noemden. Stel je weer de volgende situatie voor: in een ruimtetijd (bijvoorbeeld van Anti-de Sittervorm) is een zwart gat dat verdampt. Deze ruimtetijd heeft een rand die alle straling van het verdampende zwarte gat opvangt. Om de verstrengelingsentropie van de opgevangen straling te berekenen, moeten we dus de verstrengelingsentropie van de hele rand van de ruimtetijd weten. Wat het voorschrift van het quantum-extremale oppervlak zegt, is dat je om dat te doen een oppervlak in de AdS-ruimte moet vinden met dezelfde rand als de rand van de hele ruimtetijd. Deze rand van de rand is leeg, net zoals een boloppervlak geen rand heeft. We zoeken dus een randloos oppervlak in onze ruimtetijd. Dat oppervlak moet volgens het voorschrift ook nog eens de gegeneraliseerde entropie die je hiermee berekent minimaliseren. Die entropie bevat net zoals we eerder zagen een term die evenredig is met het oppervlak, en een term die de entropie van de materie buiten het oppervlak voorstelt.
Gedurende het tijdsverloop dat de Page-kromme beschrijft gebeurt nu het volgende. Aan het begin is het quantum-extremale oppervlak een praktisch verwaarloosbaar klein oppervlak, zodat \(S_{gen}\approx S_{mat}\). Gedurende het verdampingsproces groeit deze term. Dit gaat door totdat op de Page-tijd de balans verandert. De gegeneraliseerde entropie wordt ineens geminimaliseerd door een ander oppervlak, dat net binnen de horizon van het zwarte gat blijkt te liggen. Het verspringen van het minimaliserende oppervlak zorgt ervoor dat de term \(S_{mat}\) juist verwaarloosbaar klein wordt, en de gegeneraliseerde entropie praktisch gelijk aan het resultaat van de Bekenstein-Hawkingformule: \(S_{gen} \approx \frac{A_{hor}(t)}{4G}\). Omdat het zwarte gat verdampt, neemt deze term in de loop van de tijd juist af, totdat de verstrengelingsentropie weer nul is en de Page-kromme voltooid is.
Een wiskundige structuur
Het reproduceren van de Page-kromme is volgens sommigen een complete oplossing van de informatieparadox. De manier waarop het inzicht dat voor deze oplossing nodig was werd verkregen, de gravitationele padintegraal, blijft echter mysterieus. Die padintegraal is een soort black box die op de een of andere manier iets weet over de quantumzwaartekracht. We weten nu echter nog niets over het precieze proces waarmee de informatie ontsnapt. Hoewel er dus veel progressie is gemaakt, zijn we nog niet helemaal klaar.
Mijn scriptie is een poging om een motivatie voor het voorschrift van het quantum-extremale oppervlak te vinden, en daarmee de Page kromme te reproduceren, vanuit een heel andere, nieuwe hoek. De benaderingswijze maakt gebruik van een nieuw in zwang geraakte wiskundige structuur, die overigens al bijna honderd jaar oud is, en die perfect is voor het nauwkeurig definiëren van entropieën. Veel van de gebruikte technieken zijn ook recenter van aard, en nog recenter van aard is een nieuwe toepassing van een deel van de hierboven genoemde wiskundige structuur, namelijk de toepassing om er semi-klassieke systemen mee te beschrijven. De structuur die ik bedoel is die van operator algebra’s, of specifiek von Neumann algebra’s. Hoewel weinig mensen, zelfs onder natuurkundigen, dit weten, vormen die structuren ook de onderliggende beschrijving van quantummechanica.
Voor enige historische context: toen in de jaren 20 van de vorige eeuw Erwin Schrödinger en Werner Heisenberg beiden ongeveer gelijktijdig met een theorie van de quantummechanica op de proppen kwamen, was er een onverwacht probleem. De twee theorieën leken in vrijwel niets op elkaar, maar produceerden toch dezelfde resultaten. Schrödingers theorie was gebaseerd op golfmechanica, waarbij de toestand van een systeem wordt beschreven door een zogenaamde golffunctie die voldoet aan Schrödingers golfvergelijking, terwijl Heisenberg’s theorie gebaseerd was op tabellen (matrices) die de kansen op bepaalde energieovergangen beschreven. John von Neumann ontdekte uiteindelijk dat de onderliggende structuur de eerder genoemde Hilbertruimtes zijn: Schrödingers golffuncties zijn onderdeel van een bepaald type Hilbertruimte, en Heisenbergs tabellen zijn operatoren die op een ander soort Hilbertruimte werken. Er is een simpele transformatie tussen de twee types Hilbertruimte, waardoor ze in essentie equivalent zijn. Dat verklaart waarom zowel Schrödingers model als dat van Heisenberg tot de juiste resultaten leidde.

De onderliggende structuur die Von Neumann ontdekte, generaliseerde hij naar diverse andere soorten Hilbertruimten, met een anderssoortige ‘verstrengelingsstructuur’. In deze beschrijving zijn de operatoren van Heisenberg iets wat een wiskundige zou omschrijven als ‘elementen van een algebra die op de Hilbertruimte werken’. Afhankelijk van de precieze details kan die ‘algebra’ verschillende typen hebben, die wat zeggen over wat de precieze structuur van verstrengeling in de theorie is. De algebra’s die bij gewone quantummechanica horen, noemen we van type I, terwijl de algebra’s die bij quantumveldentheorie in een deelgebied van een ruimtetijd horen, van type III zijn. (De algebra van type II zullen we straks nog tegenkomen.) Voor dit verhaal is het enige wat van belang is dat type III-algebra’s voor onze doeleinden eigenlijk grotendeels onbruikbaar zijn. Als je een entropie wilt definiëren, dan zal die voor zulke systemen altijd oneindig zijn, en over het algemeen zijn de meeste concepten die we tot onze beschikking hebben in quantummechanica hier slecht gedefinieerd. Grotendeels daardoor is deze wiskundige structuur vrijwel onbekend onder natuurkundigen: we konden er lange tijd niets mee. Wanneer natuurkundigen spreken over entropie in quantumveldentheorie, bedoelen we vaak impliciet dat de quantumveldentheorie eigenlijk op een soort rooster in plaats van op een continuë ruimtetijd is gedefinieerd, wat de algebra weer van type I maakt en definities van entropie mogelijk maakt. Zo kunnen we toch bepaalde grootheden, zoals verschillen in entropieën, definiëren, en uiteindelijk in de berekeningen de afstand tussen de roosterpunten steeds kleiner maken zodra dat veilig is. De oneindigheden in ‘continuë’ quantumveldentheorie zeggen echter iets belangrijks over de ruimtetijd zelf. Ze zijn een consequentie van de continuïteit van de ruimtetijd. Het feit dat, wanneer die ruimtetijd helemaal continu is, veel concepten niet goed gedefinieerd zijn, suggereert dat de ruimtetijd in realiteit misschien niet helemaal continu is, en dat het concept van ruimtetijd op heel kleine lengteschalen helemaal niet goed gedefinieerd is. Met andere woorden: misschien is er sprake van emergente ruimtetijd.
Nu is recent door Edward Witten en collega’s, waaronder wederom Geoff Penington, aangetoond dat, wanneer een quantumveldentheorie niet op een vaste ruimtetijdachtergrond is gedefinieerd, maar de ruimtetijd een heel klein beetje kan fluctueren, waarmee je als het ware een klein beetje zwaartekracht ‘toevoegt’, de onderliggende algebra van type II wordt. In type II-algebra’s kunnen we wél entropieën definiëren, en voor een bepaalde subklasse van toestanden geldt zelfs dat de entropie precies de gegeneraliseerde entropie is die we moeten gebruiken, wat natuurlijk een erg bevredigende situatie is.
Hoewel we in de hoge-energiefysica deze type II-algebra’s misschien wel het minst goed kennen, hebben wiskundigen in de afgelopen eeuw op dit gebied niet stilgezeten. Dankzij wiskundigen als Vaughan Jones is er heel veel structuur in dit type algebras ontdekt, wat zelfs leidde tot belangrijke vooruitgang in de knopentheorie. Het doel van mijn scriptie was om de uit de wiskunde bekende technieken te gebruiken om de Page-kromme op een alternatieve, model-onafhankelijke manier te reproduceren, en zo een nieuwe kijk te bieden op de informatieparadox van zwarte gaten. Deze kijk maakt het zelfs mogelijk om het formalisme te koppelen aan bepaalde protocollen voor ‘quantumteleportatie’, die een diepere microscopische kijk bieden op hoe informatie uit een zwart gat ontsnapt. De hoop is dat het bekende voorbeeld van zwarte gaten zal illustreren hoe we meer in het algemeen over informatie moeten nadenken, en dat we vergelijkbare technieken wellicht kunnen toepassen in bijvoorbeeld de kosmologie.