Verhuizen in twee dimensies
Laten we beginnen met een analogie van verhuizen. Stel: je gaat verhuizen en je wilt van tevoren plannen hoe je je nieuwe huis gaat inrichten. Waarschijnlijk maak je dan een plattegrond van de verschillende kamers die je wilt inrichten. Op de plattegrond kun je vervolgens intekenen waar de bedden, banken, kasten, enzovoorts moeten komen.
Gefeliciteerd! Wat je zonet hebt gedaan is een driedimensionaal probleem versimpeld tot een tweedimensionaal probleem, door een vrijwel irrelevante dimensie (de hoogte) te negeren.
Zwarte gaten uit de jaren negentig
Een zwart gat in ons universum kent drie ruimtelijke dimensies en één tijdsdimensie. Voor deze zwarte gaten is het simpelweg te moeilijk om de effecten op een zwart gat van het uitzenden van Hawkingstraling te kunnen berekenen. Maar wat blijkt? Grofweg kan men de “wijsheid van het verhuizen” toepassen op dit probleem en twee ruimtelijke dimensies “negeren”, waardoor je wél het effect van Hawkingstraling op een zwart gat kan berekenen.
Afbeelding 1. De Event Horizon Telescope-foto van een zwart gatDeze onlangs gepubliceerde foto van een zwart gat is ook een tweedimensionale weergave van een zwart gat, maar dan in twee ruimtelijke dimensies en nul tijdsdimensies. Afbeelding: EHT Collaboration
In de jaren negentig van afgelopen eeuw werd druk gewerkt aan tweedimensonale zwarte gaten. In het bijzonder werd hieraan gewerkt door Curtis Callan, Steven Giddings, Jeff Harvey en Andrew Strominger, die in staat waren een zwart gat te beschrijven dat niet kon verdampen maar wel kon stralen; en Jorge Russo, Leonard Susskind en Laurus Thorlacius die ervoor zorgden dat het eerdergenoemde zwarte gat in het model ook kon verdampen. De hieruit volgende modellen heetten heel poëtisch het CGHS- en RST-model.
Maar let op, er zitten haken en ogen aan deze modellen!
De haken en ogen aan twee dimensies
Allereerst is het een wiskundig gegeven dat zwaartekracht in twee dimensies, één tijdsdimensie en één ruimtelijke dimensie, zich radicaal anders gedraagt dan in hogere dimensies. Om de zwaartekracht eraan te “herinneren” dat die eigenlijk zwaartekracht in drie ruimtelijke dimensies en één tijdsdimensie moet nabootsen, wordt er in het model extra materie toegevoegd die ervoor zorgt dat er überhaupt zwarte gaten kunnen zijn in twee dimensies.
Wat bedoelen we trouwens met een zwart gat in twee dimensies? Simpelweg het bestaan van een horizon, dat een gebied afbakent waaruit niks kan ontsnappen, en waarin zich ook een singulariteit bevindt. Een singulariteit is een punt in de ruimtetijd waar quantummechanische effecten dusdanig sterk zijn dat de relativiteitstheorie niet voldoende is om te beschrijven wat er gebeurt. Zie voor meer informatie over zwarte gaten ons dossier. Afbeelding 2 laat schematisch zien hoe een tweedimensionaal zwart gat ontstaat en ook weer verdampt, volgens het RST model.
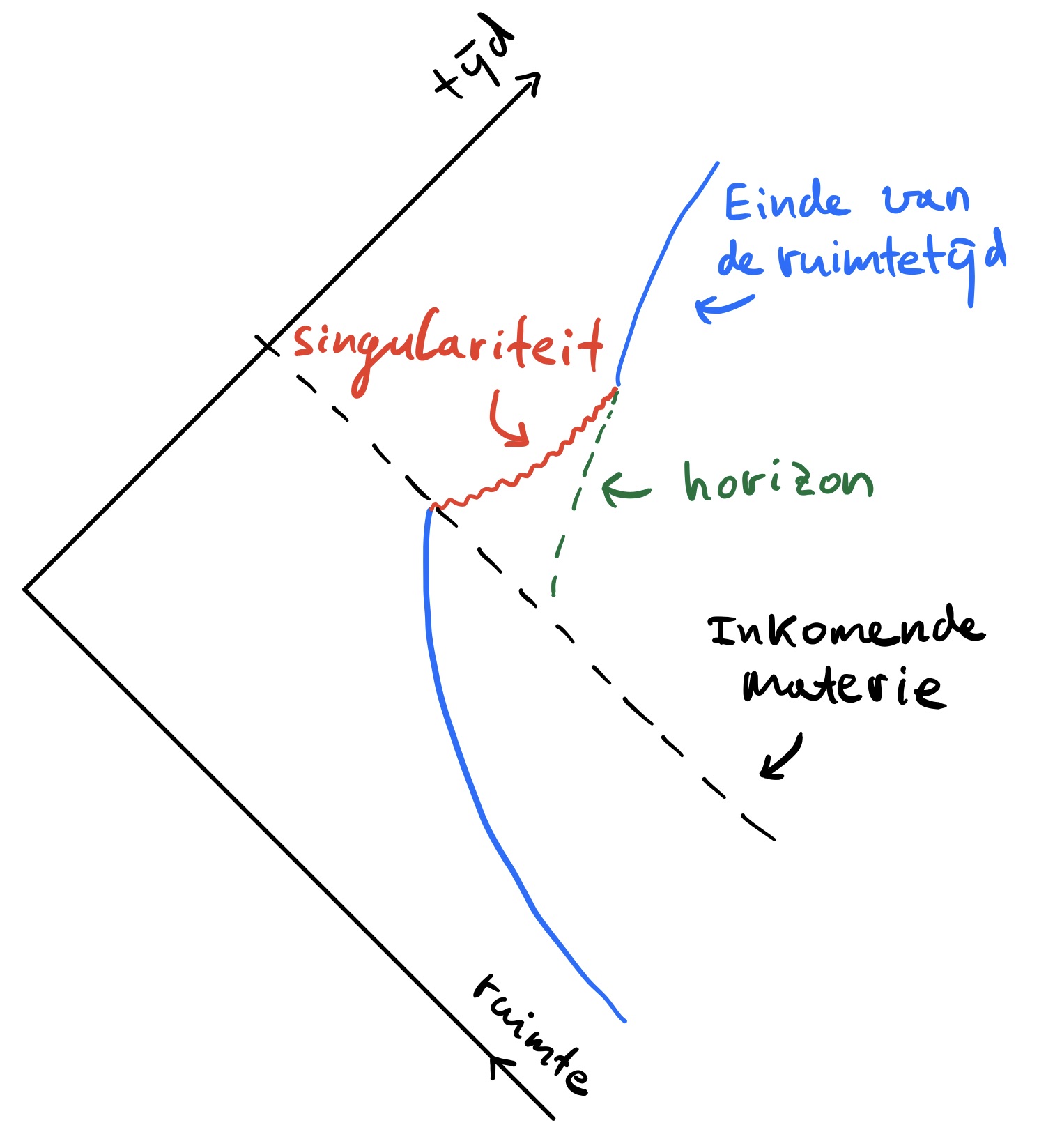
Afbeelding 2. Een zwart gat in 1+1 dimensiesDit diagram beschrijft het ontstaan en verdampen van een tweedimensionaal zwart gat volgens het RST-model. De assen geven tijd en ruimte aan. De waarneembare wereld bevindt zich aan de rechterzijde van de blauwe lijn; de aanwezigheid van deze blauwe lijn is een eigenaardigheid van het model. Op een zeker moment wordt er een sterke materiepuls het vacuüm ingeschoten (geïllustreerd met de zwarte stippellijn). Deze materiepuls is sterk genoeg om een zwart gat te vormen, wat je kan zien aan het feit dat er een singulariteit (rode lijn) ontstaat en een horizon (groene lijn). Terwijl het zwarte gat bestaat wordt er Hawkingstraling uitgezonden. Het zwarte gat verdampt van meet af aan en wanneer de horizon samensmelt met de singulariteit komt er een donderschokje vrij en ontstaat er een nieuw vacuüm.
Uit het model blijkt dat deze zwarte gaten, ook tijdens het verdampen, dezelfde temperatuur behouden en dat sommige gedeelten van de ruimtetijd worden afgesloten voor iedereen (zie de blauwe lijnen in het figuur). Dit soort rariteiten zijn te vergelijken, in de analogie met het verhuizen, met het feit dat je niet geheel je plattegrond moet vertrouwens omdat je soms bijvoorbeeld ook rekening moet houden met schuine plafonds (in de genegeerde hoogtedimensie), waarvan je tweedimensionale plattegrond geen weet heeft.
Jammer genoeg lijkt het niet mogelijk te zijn om roterende zwarte gaten na te bootsen in deze modellen, terwijl we juist verwachten dat vrijwel alle bestaande zwarte gaten roteren.
Wat vertellen tweedimensionale zwarte gaten ons?
De haken en ogen in ogenschouw nemend blijken de tweedimensionale zwarte gaten vrijwel te verdampen op een wijze zoals Hawking voorspelde. Sterker nog, ook de donderschok aan het eind van het verdampingsproces kan worden gezien in deze modellen, al blijkt dit effect niet sterk te zijn. Eerder een donderschokje dus.
Vandaag de dag zijn vergelijkbare tweedimensionale modellen in trek geraakt voor het bestuderen van wormgaten, dus wie weet wat zulke “simpele” modellen ons nog meer te vertellen hebben…!
