
Afbeelding 1. Een zwart gat.Vanaf de horizon van een zwart gat is ontsnappen niet meer mogelijk. Maar wat heeft dit met de ABC-formule te maken? Afbeelding: NASA.
Stel: iemand geeft je de meetkundige formule die nodig is om een specifiek zwart gat te beschrijven. Als je de positie wilt berekenen van de horizon, de grens van waar je niet meer aan het zwarte gat kunt ontsnappen, kan dat op twee manieren: analytisch (dus: exact) of numeriek (dus: benaderd).
Je zou kunnen beargumenteren dat één analytische oplossing meer zegt dan honderd numerieke grafieken, en dat het tevens zo is dat je in bepaalde gevallen alleen uit de voeten kunt als je een analytische uitdrukking hebt. Buiten kijf staat overigens ook dat een analytische aanpak vaak toch de meeste voldoening geeft. Dus waarom zou je niet altijd een analytische oplossing gebruiken? Er bestaat simpelweg niet in ieder geval een analytische oplossing! Helaas, pindakaas. Vaak is deze reden tot paniek een directe implicatie van de stelling van Abel-Ruffini. De stelling van wat?
Voor we in kunnen gaan op de stelling van Abel-Ruffini, moeten we eerst een beetje terminologie de revue laten passeren. Als je de meetkundige formule hebt die nodig is om een bepaald zwart gat te beschrijven, dan kun je daaruit een zogenaamde warpfactor g(x) destilleren. Bij zwarte gaten is de straal van de horizon gecodeerd in de grootste waarde van x waarvoor die warpfactor nul is. (De kleine lettertjes: het gaat hier om de reële nulpunten, en dat je de grootste waarde zoekt, is afhankelijk van je coördinaatkeuze – we zullen verderop ook een voorbeeld zien waarin juist de kleinste waarde gezocht wordt.) Een warpfactor is vrijwel altijd een polynoom. Een eenvoudig voorbeeld van een polynoom is
g(x) = 2x2 – 18.
Een willekeurig polynoom bestaat uit een eindig aantal termen waarin x tot een gehele macht is verheven, met als coëfficiënten reële getallen voor de x-termen. De waarde van x zelf mag een complex getal zijn. De graad van een polynoom is de hoogste macht van x die voorkomt. Het polynoom g(x) hierboven is dus van graad 2.
Je spreekt van een nulpunt wanneer er een waarde van x is zodat het polynoom gelijk is aan nul. De hoofdstelling van de algebra luidt: “een n-de graads polynoom heeft n nulpunten”. Over de exacte locaties van deze nulpunten zwijgt deze hoofdstelling echter in alle toonaarden.. en dat is precies wat wij nou juist willen weten! We willen immers een formule hebben waarmee we het grootste reële nulpunt van de warpfactor kunnen bepalen.
Laten we weer eens kijken naar ons voorbeeldpolynoom g(x). De tweedegraadsheid van dit polynoom verklapt dat er twee nulpunten zijn, dankzij de hoofdstelling van de algebra. Door goed naar het polynoom te kijken, of wat waarden te proberen, vinden we al snel dat de nulpunten x=3 en x=-3 moeten zijn.
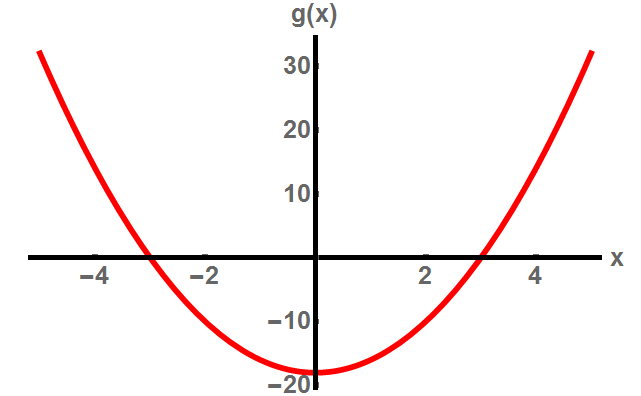
Afbeelding 2. Het polynoom g(x).Een grafiek van het polynoom g(x) = 2x2 – 18. We zien dat de nulpunten bij x=3 en x=-3 liggen.
Als we nu bijvoorbeeld de term 13 x toevoegen aan g(x) blijft het een 2e-graads polynoom, maar de nulpunten veranderen, en zijn niet meer zo eenvoudig te vinden als voorheen. Gelukkig hebben we de welbekende abc- of wortelformule om voor ons de kastanjes uit het vuur te halen. Die formule geeft mooi de nulpunten voor een willekeurig polynoom van graad 2 in termen van de coëfficiënten van het polynoom.
Nu bstaan er voor de 3e graad en de 4e graad ook formules die hetzelfde bereiken als de ABC-formule. Deze uitdrukkingen zijn vernoemd naar respectievelijk Cardano en Ferrari. (Waarschijnlijk klonken abcd- en abcde-formule een beetje té veel als Sesamstraat-items…) Deze formules stammen uit de 16e eeuw. Velen hebben getracht eenzelfde resultaat te verkrijgen voor polynomen van 5e en hogere graad, maar tevergeefs. Uiteindelijk werd in de loop van de 19e eeuw de stelling van Abel-Ruffini bewezen, die zegt dat er voor 5e– en hogere graads polynomen geen enkele formule bestaat die de waarde van de nulpunten geeft! Het bewijs maakt gebruik van Galoistheorie, een theorie waarin types van polynomen en nulpunten kunnen worden geclassificeerd.
Om dus de implicatie van de stelling te benadrukken: er zijn wel 5e-graads polynomen waarvoor we de nulpunten kunnen bepalen, zoals bijvoorbeeld x5-1 (waarvoor x=1 een nulpunt is) maar voor een willekeurig polynoom bestaat er geen uitdrukking voor de nulpunten in termen van de coëfficiënten van het polynoom. Dit betekent ook dat een ongelooflijk sterke computer in vrijwel alle gevallen onmogelijk analytische oplossingen kan vinden! Het vinden van een numeriek benaderde oplossing is echter geen enkel probleem.
Wat was ook alweer de connectie met zwarte gaten? Laten we het voorbeeld van een geladen zwart gat in een willekeurig aantal ruimtelijke dimensies, d, beschouwen. (De wetenschappelijke achtergrond is in dit artikel te vinden.) Dit zwarte gat heeft een warpfactor gegeven door het polynoom
g(x) = 1 – 2 M xd-2 + Q2 x2d-4.
Hierin is het getal M de massa van het zwarte gat, en Q de lading. De coördinaten zijn zodanig gekozen dat in dit geval het kleinste nulpunt je de straal van de horizon geeft. Merk op dat de stelling van Abel-Ruffini je vertelt dat je voor dimensies hoger dan vier geen analytische formule meer hebt om de nulpunten te bepalen: in vijf dimensies (d=5) heeft het bovenstaande polynoom graad 6. Wederom: helaas, pindakaas.

Afbeelding 3. Niels Henrik Abel(1802-1829).Abel voltooide in 1824 het bewijs van de stelling waaraan Paolo Ruffini in 1799 begonnen was. De stelling is daarom naar beide wiskundigen vernoemd.
Misschien lijkt het beschrijven van een zwart gat in vijf dimensies of meer je sowieso al niet erg nuttig – onze ruimte heeft immers maar drie dimensies! Toch zijn er allerlei natuurkundige modellen, zoals bijvoorbeeld de snaartheorie, waarin dit soort hogerdimensionale zwarte gaten een rol spelen.
Voor dit en vele andere soorten zwarte gaten met polynomiale warpfactor, die bijvoorbeeld ook voorkomen in de context van holografie, moet je dus op je hoede zijn voor de stelling van Abel-Ruffini. Die stelling vertelt je vanaf wanneer je je pen en papier aan de wilgen moet hangen en je numerieke computervaardigheden uit de kast moet halen. Een duidelijke boodschap van de wiskunde: leuker kunnen we het niet maken, makkelijker ook niet…