
Wat we niet begrijpen aan zwaartekracht
Sinds het einde van de zeventiende eeuw begrijpen we al goed dat zware dingen elkaar aantrekken en dat deze aantrekkingskracht (ook wel zwaartekracht genoemd) zich op een regelmatige manier gedraagt. Dit gedrag wordt beschreven door de zwaartekrachtsformule van Newton. Deze formule werd in 1916 door Albert Einstein aangepast: met zijn algemene relativiteitstheorie liet Einstein zien dat zwaartekracht zich op grote schalen anders gedraagt dan we in eerste instantie dachten. Tot de dag van vandaag is deze relativiteitstheorie – maar ook Newtons formule – van onschatbare waarde gebleken. Met de relativiteitstheorie berekenen we bijvoorbeeld hoe we een raket de ruimte in moeten sturen, met de wet van Newton hoe stevig we een brug moeten maken zodat deze niet instort.
Tegelijkertijd met Einsteins werk aan de wetten van de zwaartekracht was er een heel andere ontwikkeling gaande in de theoretische natuurkunde. Deze ontwikkeling richtte zich op de natuur in het klein. En met klein bedoelen we hier héél klein: men probeerde een theorie te vinden voor de bouwstenen van ons universum, zogenaamde elementaire deeltjes, die we met het blote oog en de beste microscopen van de wereld niet kunnen zien. Dit onderzoek leidde uiteindelijk tot een theorie die we nu quantummechanica noemen. De quantummechanica is een voorbeeld van een microscopische theorie (een wat gekke naam, omdat het hier dus gaat over dingen die we met een microscoop juist niet kunnen zien). Zo’n theorie laat zien hoe verschijnselen die we wél met het blote oog kunnen zien, zoals elektrische en magnetische krachten, voortkomen uit het gedrag van een klein aantal fundamentele bouwblokken.
Je zou kunnen zeggen dat de wetten van de zwaartekracht en de quantummechanica zich met verschillende dingen bezighouden. Zwaartekracht wordt pas belangrijk zodra dingen heel zwaar zijn – denk hierbij aan de aantrekkingskracht tussen een raket en een planeet. De elementaire deeltjes die we hierboven noemden zijn over het algemeen zo licht dat we deze aantrekkingskracht kunnen verwaarlozen. Daarom kunnen beide theorieën, de relativiteitstheorie en de quantummechanica, goed naast elkaar leven. Er zijn echter bepaalde verschijnselen in ons universum waarbij extreem veel massa op één plek is gelokaliseerd. Een bekend voorbeeld van zo’n verschijnsel is een zwart gat. Het blijkt dat deze zwarte gaten heel vreemde eigenschappen hebben die we met de huidige theorieën niet kunnen verklaren. Een zo’n hardnekkig probleem is de informatieparadox die al recent is besproken in dit artikel.
Een manier om zwarte gaten te begrijpen, en het daarbij horende informatieprobleem op te lossen, is door een theorie te vinden die de quantummechanica en Einsteins theorie verenigt: een theorie van quantumzwaartekracht. Zo’n theorie zou – op dezelfde manier als voor elektrische en magnetische verschijnselen – de volgende vraag moeten beantwoorden: wat is de microscopische beschrijving van zwaartekracht? Een recent antwoord op deze vraag is dat zwaartekracht wellicht niet één microscopische beschrijving heeft, maar moet worden gezien als een soort gemiddelde van een heel scala van zulke theorieën.
Zwaartekracht als een matrixensemble
Om dit idee verder uit te leggen beginnen we met het spelen van een kansspel. We gooien een muntstuk op en verbinden daar een weddenschap aan. Als de munt op kop terechtkomt betaal ik jou twintigduizend euro. Als de uitkomst ‘munt’ wordt betaal jij mij tienduizend euro. Een goede deal, zou je zeggen, maar wel een met een groot risico. De kans is 50% dat de uitkomst munt wordt en dat je daarmee tienduizend euro moet betalen. Dit is een risico dat voor de meesten van ons zo groot is dat we niet aan dit spel zouden meedoen.

Het risico kan enorm worden verkleind door een klein aanpassing te doen aan het spel. In plaats van het eenmaal opgooien van een muntstuk met een uitkomst van tienduizend of twintigduizend euro, kunnen we ook tienduizend keer een muntstuk opgooien met een uitkomst van één of twee euro bij iedere worp. Op deze manier wed je niet met al je geld op hetzelfde paard en is het mogelijk om goede voorspellingen over de uitkomst te kunnen doen. Het is nu zo goed als zeker dat je na deze tienduizend worpen ongeveer vijfduizend euro hebt verdiend: je verdient zo’n vijfduizend keer twee euro, en verliest er zo’n vijfduizend keer één. Het is daarom zeker aan te raden om aan dit tweede spel mee te doen! Je loopt de grote winst van twintigduizend euro bij het eerste spel mis, maar je hebt het risico om te verliezen met het tweede spel tot bijna nul gebracht.
De bovenstaande weddenschap is bedoeld als illustratie van wat wiskundigen een statistisch gemiddelde noemen: ondanks dat ik de uitkomst van één worp van een muntstuk niet kan voorspellen, weet ik wel met grote zekerheid dat als ik deze worp heel vaak (zeg zo’n tienduizend keer) herhaal, grofweg de helft van deze worpen kop zal geven en de andere helft munt. Door iets maar vaak genoeg te herhalen, middel je het toeval eruit1. De gemiddelde grootheden kunnen wel met goede zekerheid worden voorspeld. Maar wat heeft de bovenstaande weddenschap met zwaartekracht te maken?
In de lente van 2019 hebben drie natuurkundigen, Phil Saad, Steve Shenker en Douglas Stanford van de universiteiten van Stanford en Princeton, een interessant artikel gepubliceerd waarin ze een voorstel doen voor hoe zwaartekracht2 zich op een microscopische schaal gedraagt. Grof gezegd is hun idee dat zwaartekracht ontstaat door een ‘muntstuk heel vaak op te gooien’. Om precies te zijn wordt de rol van het muntstuk gespeeld door wat we een toevalsmatrix noemen. Toevalsmatrices en hun toepassingen binnen de natuurkunde hebben we al eerder besproken in deze reeks artikelen. Het idee is dat de Hamiltoniaan van onze microscopische theorie, de wiskundige grootheid die de energie van een systeem bepaalt en die we normaalgesproken vast kiezen, voor zwaartekracht misschien wel van het toeval afhangt. Dit zou betekenen dat er niet één microscopische theorie van zwaartekracht is, maar dat we zwaartekracht moeten zien als een soort gemiddelde van een heel ensemble van microscopische theorieën. Hoe komen we erachter of de microscopische theorie van zwaartekracht inderdaad een kop-of-muntspel met ons aan het spelen is?
Wormgaten en statistische variantie
Naast de gemiddelde uitkomst is er nog een ander begrip dat belangrijk is om een kansproces te beschrijven: de statistische variantie. Deze variantie geeft aan hoe groot de typische afwijking van het gemiddelde is. Bij het heel vaak opgooien van een munt is het niet altijd zo dat je precies de helft van de keren kop gooit: dit varieert enigszins door het toeval. Hoe groter deze wisselingen rondom het gemiddelde, hoe groter de variantie. In ons voorbeeld met de munt is de variantie bij één keer gooien voor tien- of twintigduizend euro bijvoorbeeld veel groter dan bij tienduizend keer gooien voor een of twee euro.
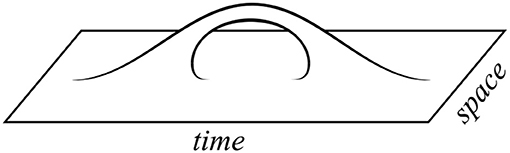
Als zwaartekracht inderdaad overeenkomt met gemiddelden van een microscopisch toevalsproces, dan zou je je kunnen afvragen hoe we de variantie van dit proces moeten interpreteren. Het blijkt dat we in een zwaartekrachtstheorie een goede kandidaat hebben voor deze interpretatie: variantie lijkt sterk verbonden met sluiproutes in het heelal, zogenaamde wormgaten. In afbeelding 1 is zo’n route weergeven: je kunt over een wormgat nadenken als een ‘brug’ tussen twee plekken in ons heelal die op het eerste gezicht ver van elkaar weg liggen. In sciencefictionfilms worden wormgaten dan ook vaak gebruikt om snel van een plek in het heelal naar een andere plek te reizen. Hier kun je lezen of zoiets daadwerkelijk kan, en hoe je in dat geval een wormgat gebruikt om zo’n reis te ondernemen.
Meer algemeen kijken de auteurs van het Stanford/Princeton-artikel naar een fictief heelal met niet-triviale topologie3. In afbeelding 3 is een tweedimensionaal voorbeeld van zo’n heelal weergeven: het ‘handvat’ in dit plaatje komt overeen met het wormgat. Je kunt in dit heelal op twee manieren van links in het plaatje naar rechts in het plaatje reizen: via het ‘handvat’, of gewoon door de platte ruimte. In tegenstelling tot in de sciencefiction is de route via het wormgat hier overigens niet sneller of korter.
Het idee is nu dat we dergelijke verbindingen in het heelal kunnen interpreteren als ontstaan door de variantie in het microscopische toevalsproces. Dit kan het duidelijkst worden uitgelegd met behulp van afbeelding 4. We hebben twee extra ingrediënten nodig om het idee van de Stanford/Princetongroep duidelijk te maken. Allereerst werken ze in een theorie van tweedimensionale zwaartekracht (om precies te zijn in een heelal met constante negatieve kromming, ook wel Anti-de Sitterruimte genoemd). Dit betekent dat de zwaartekrachtsberekeningen plaatsvinden op tweedimensionale oppervlakken. Een belangrijk voorbeeld van zo’n oppervlak, dat we in het vervolg zullen bekijken, is de schijf. Een tweede ingrediënt is de AdS/CFT-correspondentie, die ons vertelt waar de informatie van de microscopische theorie is gelokaliseerd in de ruimtetijd. Deze correspondentie vertelt ons dat voor zwaartekracht in de Anti-de Sitterruimte (AdS) de microscopische theorie (in dit geval is dat een ‘conforme veldentheorie’, oftewel een CFT) op de rand van de ruimtetijd leeft, in één dimensie minder. Een dergelijke beschrijving van zwaartekracht met behulp van minder dimensies is een voorbeeld van het holografisch principe. Voor een tweedimensionaal schijfje is de rand waar het om gaat een eendimensionale cirkel.
Stel dat we beginnen met onze tweedimensionale schijf en geïnteresseerd zijn in een bepaalde grootheid in de microscopische theorie, bijvoorbeeld het spectrum van verschillende energieën die het systeem kan hebben. (In het artikel bekijken de auteurs de zogenaamde partitiefunctie, die gerelateerd is aan die energieën via een bepaalde transformatie.) Uit de bovengenoemde AdS/CFT-correspondentie weten we dat we deze berekening in de theorie op de rand van de schijf (in dit geval: een cirkel) kunnen doen. Het antwoord dat hieruit komt is een bepaald getal. We kunnen ook twee kopieën van deze cirkel, aangegeven met rood en blauw in afbeelding 4, bekijken en dezelfde berekening doen. Met behulp van een kleine extra technische aanname – namelijk dat de microscopische theorie deterministisch is – kunnen we die berekening doen, en krijgen we een logisch antwoord: twee keer het antwoord dat we bij één enkel schijfje vonden. In de zwaartekrachtstheorie hebben we daarmee een oppervlak beschreven dat uit twee losse stukken bestaat, een schijfje met een rode rand en een schijfje met een blauwe rand. Zie afbeelding 4 (boven), waarin we de schijfjes als gekromde ‘hoedjes’ hebben getekend; in een zwaartekrachtstheorie kan de ruimte allerlei vormen aannemen en dus zijn de schijfjes die we met de theorieën op de rand beschrijven niet alleen plat! Juist de vorm die we hier getekend hebben sluit goed aan bij wat we hierna willen doen.
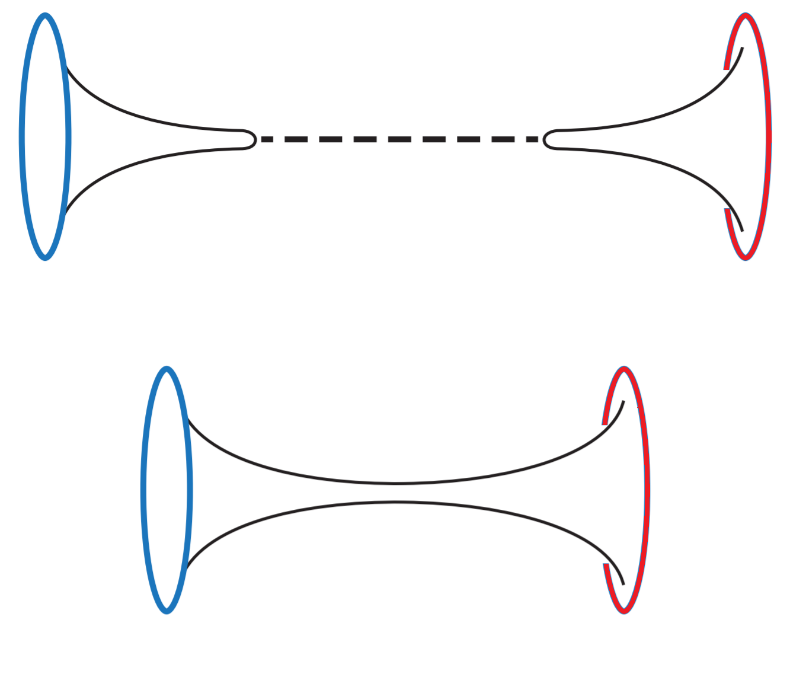
Tot zover gaat alles goed: we hebben aan de hand van de rand (de twee cirkels) de zwaartekracht in een gekromd heelal (de twee vervormde schijfjes) weten te beschrijven. Het probleem is echter dat er in deze zwaartekrachtstheorie nóg een oppervlak is dat als rand zowel de rode als de blauwe cirkel heeft, namelijk een wormgat dat beide met elkaar verbindt, zoals te zien in afbeelding 4 (onder). Ook een dergelijk heelal zou dus aan de hand van de theorie op de twee cirkels beschreven moeten kunnen worden! Hoe moeten we dit wormgat interpreteren in termen van de twee microscopische theorieën op de rand? Dit is waar het toeval een belangrijke rol speelt. Het idee van de Stanford/Princetongroep is dat we dit wormgat kunnen beschrijven aan de hand van de variantie van een kansproces. Zodra we de microscopische theorie van het toeval laten afhangen (door van de Hamiltoniaan een toevalmastrix te maken) hangen de natuurkundige grootheden zoals energie ook van het toeval af. Er zijn nu wiskundig gezien twee verschillende manieren waarop we de resultaten van een toevalstheorie op één cirkelvormige rand kunnen combineren tot de resultaten van een toevalstheorie op twéé cirkelvormige randen. In detail: het wormgat in afbeelding 4 (onder) komt overeen met het gemiddelde van het kwadraat van de oorspronkelijke grootheid (in dit geval is die grootheid de partitiefunctie). De schijven zonder verbinding in afbeelding 4 (boven) berekenen daarentegen het kwadraat van het gemiddelde van de grootheid. Zodra de grootheid waarin we geïnteresseerd zijn van het toeval afhangt geven deze berekeningen – het kwadraat van het gemiddelde en het gemiddelde van het kwadraat – niet hetzelfde antwoord. Het verschil is precies de variantie4!
Bovenstaande beschrijving is behoorlijk technisch, maar wat de auteurs uiteindelijk aantonen is een heel fysisch resultaat: de aanwezigheid van wormgaten in een theorie van zwaartekracht duidt erop dat we inderdaad te maken hebben met een statistisch ensemble van microscopische theorieën, waarin zwaartekracht een kansproces is.
Concluderend: in dit artikel hebben we een recente ontwikkeling binnen de natuurkunde besproken waarbij zwaartekracht op microscopisch niveau niet beschreven wordt door één theorie, maar door een gemiddelde van zulke theorieën Deze nieuwe kijk op zwaartekracht kan nuttig zijn om bepaalde eigenschappen van zwarte gaten, zoals de informatieparadox, beter te begrijpen. We moeten echter niet vergeten dat deze ontwikkeling nog steeds in de kinderschoenen staat – zo heeft de Stanford/Princetongroep alleen gekeken naar een heel specifiek ‘toy’ model van zwaartekracht in twee dimensies, en zijn daadwerkelijke wormgaten in ons eigen heelal nog nooit waargenomen. Er wordt daarom op dit moment nog hevig gediscussieerd binnen de natuurkundige gemeenschap of dit inderdaad een nuttige manier is om zwaartekracht te beschrijven, of dat de aanwezigheid van het toeval voortkomt uit de modelkeuze in dit artikel – ons eigen universum heeft bijvoorbeeld niet twee maar wel vier ruimtetijddimensies, en het is dus niet direct duidelijk of de zwaartekracht in ons heelal aan dezelfde wetten voldoet. Wat we aan het idee van Saad, Shenker en Stanford hebben als het gaat om het beschrijven van de ‘echte’ zwaartekracht moet dus nog blijken, maar hoe het ook zij: nieuwe ideeën als dit geven ons steeds weer andere manieren om tegen zwaartekracht aan te kijken, en helpen ons zo weer een stapje verder in onze zoektocht naar een quantumtheorie van de zwaartekracht in ons heelal.
[1] Dit fenomeen staat in de statistiek ook wel bekend als de ‘wet van de grote getalen’.
[2] Om precies te zijn bekijken de auteurs in hun artikel een model voor zwaartekracht in twee dimensies, de zogenaamde Jackiw-Teitelboimzwaartekracht.
[3] Dit betekent dat er een lus in de ruimtetijd zit die je niet kunt samentrekken tot een punt.
[4] De variantie van een toevalsvariabele X bereken je met formule Var(x) = E(X2) – E(X)2, waarbij E de verwachtingswaarde is.