
Diffractie treedt op wanneer golven om een object heen bewegen, of door een gat in een object. In het eerste geval kan je je voorstellen dat een licht1golf tegen een object aanbotst en de golf in tweeën splitst, waarbij de helft linksom gaat en de andere helft rechtsom. Vervolgens combineren de golven aan de andere kant weer, waarbij ze met elkaar interfereren. Dat wil zeggen: daar waar beide golven een piek of beide golven een dal hebben versterken ze elkaar, zogenoemde constructieve interferentie, maar daar waar de ene golf een piek heeft en de ander een dal, heffen ze elkaar op, wat we destructieve interferentie noemen. Zo ontstaat achter het object een zogenaamd interferentiepatroon, zoals te zien in afbeelding 2.
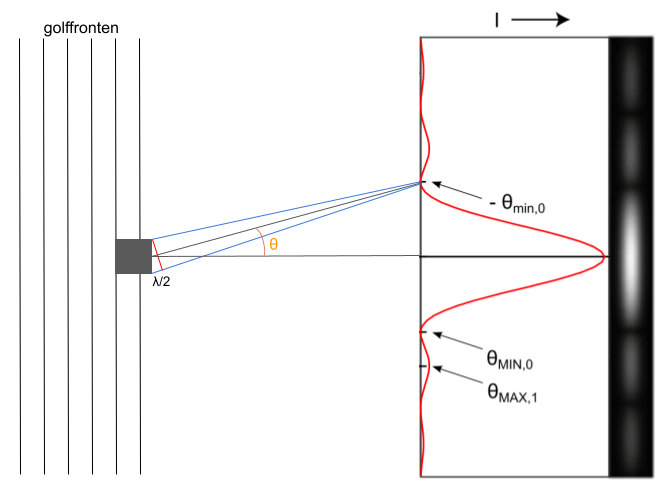
Zo’n patroon ontstaat doordat de twee golven een andere afstand moeten afleggen. Wanneer een van de golven een geheel aantal golflengtes meer of minder afstand moet afleggen is er constructieve interferentie, en wanneer er een verschil is van nog een halve golflengte meer of minder in de afstand die ze afleggen, dan is er destructieve interferentie. Daardoor vindt er op een scherm achter de obstructie afwisselend constructieve en destructieve interferentie plaats en is er dus afwisselend veel of weinig licht.
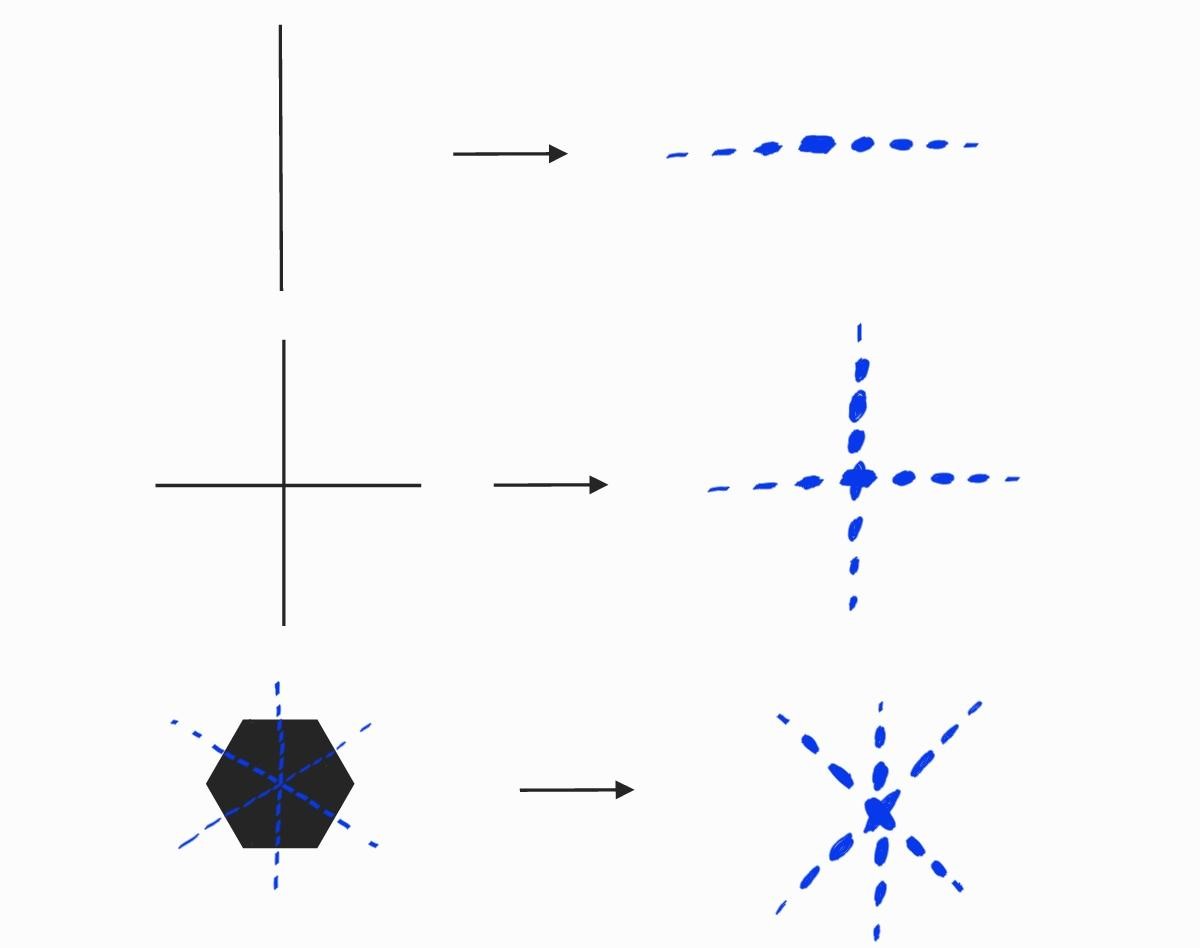
Daarnaast is er het verschijnsel dat, wanneer een lichtbron meerdere kleuren licht en dus meerdere golflengtes uitzendt, de verschillende golflengtes licht andere afstanden hebben tussen de pieken en dalen van hun interferentiepatroon. Dat resulteert in een regenboogpatroon als de verschillende golflengtes het zichtbare spectrum omvatten. Ten slotte, en hier het meest van belang: wanneer je het object waartegen het licht valt (of het gat waar het licht doorheen schijnt) een andere vorm geeft, krijgt het interferentiepatroon ook een andere vorm, zoals te zien in afbeelding 3.
Om te begrijpen hoe diffractie de kruisjes op sterrenfoto’s veroorzaakt, moeten we het eerst hebben over hoe zo’n telescoop werkt. De manier waarop telescopen zoals de Hubbletelescoop of de JWST grofweg werken, is dat er een grote, subtiel gebogen spiegel is die zo veel mogelijk licht opvangt en dat allemaal reflecteert in de richting van een kleinere spiegel die het weer terugreflecteert door een gat in het midden van de grote spiegel. Daar wordt het licht in beelden omgezet. Voor de JWST zien we deze constructie in afbeelding 4. De kleinere spiegel moet met houders op de juiste plek ten opzichte van de grote spiegel vastgehouden worden. Wat gebeurt er als het licht om deze houders heen beweegt? Juist: diffractie!

De Hubbletelescoop heeft vier armen die de kleine spiegel op zijn plek houden en samen een kruis vormen. Dat verklaart dus het vierpuntige interferentiepatroon dat te zien is op de Hubble foto’s – zie afbeelding 5. Bij de foto’s van de JWST, zoals die in afbeelding 1, heeft het interferentiepatroon juist acht punten – zes grote en twee kleinere. Hierdoor kan je eenvoudig aan sterrenfoto’s herkennen of ze met de Hubbletelescoop of met de JWST zijn gemaakt – dat merkten we ook al op in dit artikel. Wordt de kleine spiegel van de JWST dan met acht armen vastgehouden? Nee, dat zou wat overdreven zijn. Bij de JWST komen zes van de acht punten (de grootste punten) van diffractie tegen de grote spiegel zelf. Deze is namelijk opgebouwd uit regelmatige zeshoeken, zoals te zien in afbeelding 6. We hebben eerder gezien dat regelmatige zeshoeken een zespuntig interferentiepatroon geven. De twee extra punten komen door de drie armen die de kleine spiegel van de JWST vasthouden. Die zijn zo uitgelijnd dat één van de punten overlapt met een van de punten die resulteren uit de diffractie tegen de spiegels; de andere twee armen zie je dus in het interferentiepatroon terug.

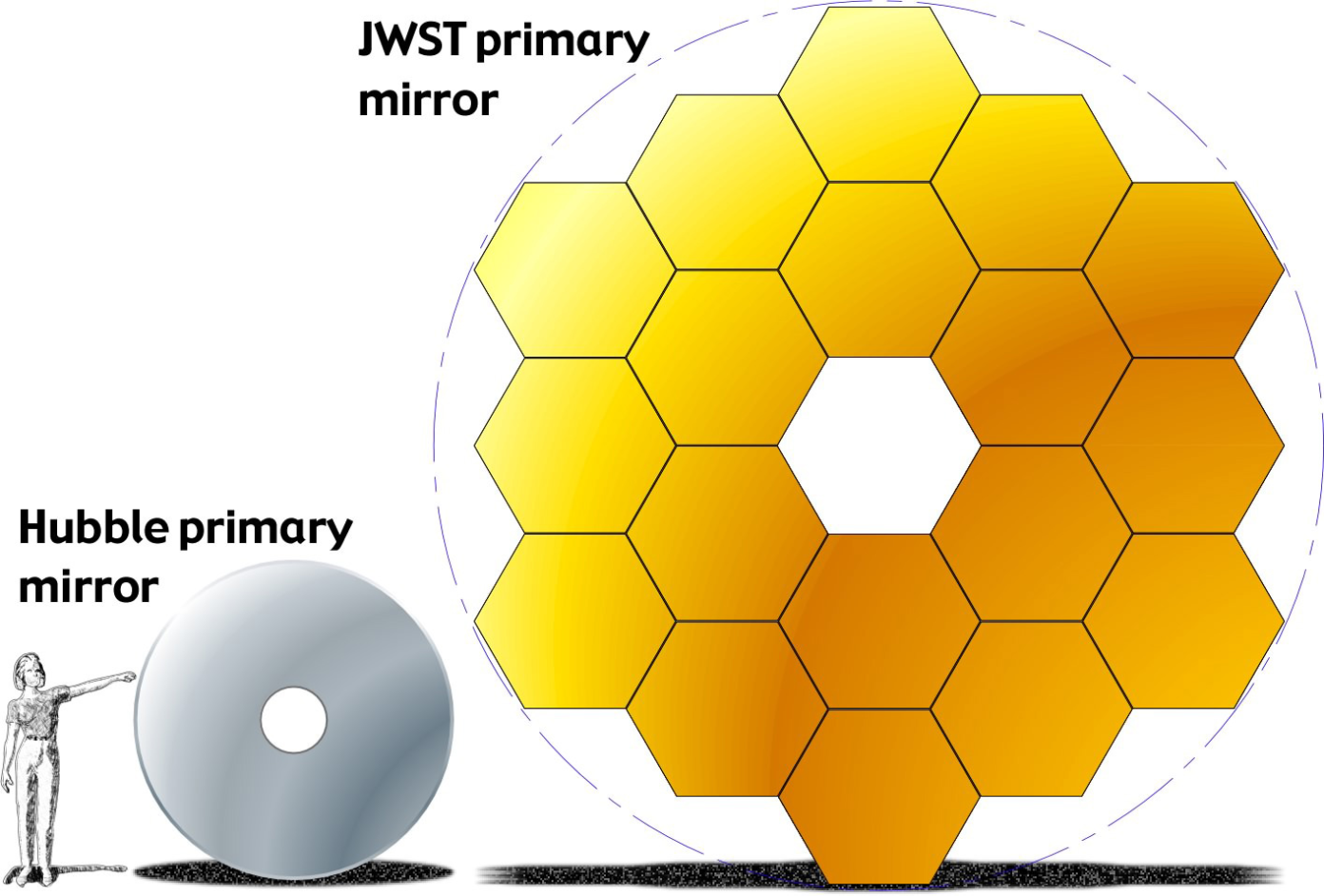
Je kan je afvragen waarom de constructeurs in hemelsnaam een spiegel uit regelmatige zeshoeken hebben gebouwd, als dat zo’n groot effect heeft op het beeld. Je moet je echter realiseren dat de doorsnede van de gehele spiegel 6,5 meter is, en dat je zoiets niet zomaar de ruimte in schiet. De spiegel moest daarom uit segmenten bestaan die opgevouwen kunnen worden, en die wanneer ze zijn uitgevouwen naadloos op elkaar aansluiten. Op die manier zitten er geen gaten in de spiegel en vormen de onderdelen vervolgens samen ongeveer een cirkel. Dat is van belang, aangezien alleen een cirkelvormige spiegel het beeld zo focust dat het niet in een bepaalde richting vervormd wordt. Regelmatige zeshoeken zijn hiervoor de ideale kandidaat.2
Ten slotte: hoe kan het nu dat we dit effect ook vaak met gewone camera’s zien, en zelfs met het blote oog – niet alleen bij sterren, maar ook bijvoorbeeld bij lampen? Het effect bij een camera is simpel te verklaren. Zoals eerder gezegd treedt diffractie ook op wanneer het licht door een gat heen moet, zoals de lensopening van een camera. Ook die kan natuurlijk een bepaalde vorm hebben; in een camera is het vaak het verstelbare diafragma dat niet rond maar hoekig is. Bij onze ogen ligt het net anders. De lenzen van onze ogen bevatten kleine imperfecties en lijnen waar de vezels van het organische materiaal samenkomen, en ook die zorgen voor diffractie. Dat imperfecties in onze ogen van persoon tot persoon verschillen zorgt ervoor dat, hoewel iemand bij alle sterren hetzelfde kruisje ziet3, alle mensen dat kruisje wel op een net andere manier zien. Hoe kijk jij naar de sterren – als Hubble, of als de JWST?
[1] Dit effect geldt overigens voor alle soorten golven, en ook voor deeltjes, aangezien die zich ook als golf kunnen gedragen. Dit verhaal komt je daarom misschien wel bekend voor als je wel eens over het bekende tweespletenexperiment hebt gelezen, waarover ik het in mijn vorige artikel ook al had.
[2] Daarnaast versimpelen de zeshoeken ook aanzienlijk het uitlijningsproces.
[3] Probeer de volgende keer als je naar de sterren kijkt eens of je een verschil kan zien als je ofwel je linker ofwel je rechteroog sluit. Aangezien je ogen onderling ook verschillen, zou je dan ook twee verschillende kruisjes moeten zien, hoewel het verschil misschien klein is.