
Afbeelding 1. Een donkere steeg.Een donkere steeg – een goede bron van inspiratie. Foto: Franck Michel.
Inleiding
Ergens aan het begin van de twintigste eeuw werd de Hongaarse wiskundige George Pólya wakker in een tochtige steeg in het midden van een vreemde stad. Het was nacht en de donkere straten om hem heen kwamen hem niet bekend voor. Hij staarde enige momenten verward voor zich uit, maar kon zich met geen mogelijkheid herinneren waar hij was of hoe hij daar terechtgekomen was. Gelukkig was George warm gekleed en had hij een knapzak vol proviand bij zich.
Vol goede moed ging hij op stap, liep het steegje uit en kwam aan bij een kruising. George moest nu een keuze maken: ging hij rechtdoor, sloeg hij rechts- of linksaf of kon hij beter rechtsomkeert maken? Hij had nog geen flauw idee welke richting hij op moest, maar gelukkig had hij had een heilig vertrouwen in de wetten van de wiskunde.
Onder het licht van een eenzame lantaarn begon hij vlug wat formules in zijn trouwe notitieboekje te krabbelen. Nadat hij enkele pagina’s gevuld had met berekeningen klaarde zijn gezicht op. Hij stopte zijn notitieboekje veilig weg in de binnenzak van zijn jas, en met het volste vertrouwen sloeg hij een willekeurige straat in. Een stuk verderop kwam hij nog een kruising tegen, en ook daar koos hij een willekeurige afslag, en evenzo bij de volgende kruising.

Afbeelding 2. George Pólya.Pólya op zijn veilige, oude dag. Foto van Wikipedia.
En inderdaad, na enige tijd stevig doorstappen vond Pólya zijn veilige huis weer terug. Eenmaal uitgeslapen en verfrist schreef hijeen artikel over zijn belangrijke inzicht: als hij bij elke kruising een willekeurige afslag zou nemen, was het gegarandeerd dat hij op een zeker moment terug bij zijn huis zou komen.
Verbazingwekkend genoeg brengen zulke ‘toevalswandelingen’ je alleen terug bij je beginpunt als je loopt over een ééndimensionale lijn of over een tweedimensionaal vlak, zoals het stratenplan van een stad. In drie en meer dimensies kom je met deze strategie naar alle waarschijnlijkheid nooit meer terug bij je beginpunt. Een verwarde vogel is dus al snel verder van huis!
Een grove uitleg
Het bovenstaande verhaal is natuurlijk verzonnen, maar het wiskundige inzicht klopt wel degelijk. Om te zien hoe George Pólya tot dit inzicht kwam, is het handig om eerst over een eenvoudiger voorbeeld na te denken. Stel je een verwarde wiskundige voor die zich in een iets eenvoudigere situatie bevindt: ze is de weg kwijt in een lange straat zonder zijstraten of kruisingen. Haar huis is ergens in deze straat, ze weet alleen niet welke kant op. Dit is de ééndimensionale variant van het probleem dat hierboven in twee dimensies geschetst werd, en dit zou volgens Pólya’s berekeningen ook een gelukkig einde moeten hebben.

Afbeelding 3. Een ééndimensionaal ‘stratenplan’.Het beginpunt en het aantal stappen tot dat punt zijn in het diagram aangegeven. Afbeelding door de auteur.
Op elk moment kan onze proefpersoon een stap vooruit of achteruit nemen, en deze keuze wordt willekeurig gemaakt: ze gooit elke keer een munt op en stapt vooruit bij kop en achteruit bij munt. De kans dat ze vooruit stapt is dus 1/2. Laten we er voor het gemak van uitgaan dat de proefpersoon voor haar huis vertrekt, maar dat zelf nog niet door heeft.
Wat is de kans dat ze na 2n stappen met behulp van deze toevalswandeling weer thuis komt? Daarvoor is het nodig dat n van die stappen vooruit zijn, en de resterende n achteruit. De kans dat ze eerst n stappen vooruit zet en daarna n achteruit, is dus bijvoorbeeld
![]()
Het maakt echter niet uit in welke volgorde ze de stappen zet. Het aantal mogelijke manieren om n stappen voorwaarts te kiezen uit in totaal 2n stappen kan geteld worden met een binomiaalcoefficiënt,
![]()
Hierin is n! , of n-faculteit, de gebruikelijke wiskundige notatie voor n × (n-1) × (n-2) × … × 2 × 1. De totale kans dat de wiskundige na 2n stappen weer terug is, qn, is dus het product van de bovenstaande twee uitdrukkingen:
![]()
De vraag is natuurlijk wat er gebeurt als het aantal stappen groot wordt: kom je dan thuis, of ben je voor altijd verloren? Om dit te zien in ons ééndimensionale probleem kunnen we kijken naar de som van al deze kansen, q:
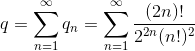
Deze som is nogal lastig uit te rekenen, maar voor een groot aantal stappen kunnen we de faculteiten benaderen met behulp van Stirlings benadering:
![]()
Hoe deze benadering precies tot stand komt is misschien een interessant onderwerp voor een volgend artikel, maar voor nu kunnen we ervan uit gaan dat deze goed werkt. Onze som van kansen wordt dan bij benadering
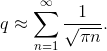
Deze uitdrukking divergeert: als we de som proberen uit te rekenen, zien we dat de waardes van de opeenvolgende termen niet snel genoeg kleiner worden om het feit te compenseren dat we een oneindige hoeveelheid van deze termen bij elkaar optellen. De kans dat de verstrooide wiskundige op een bepaald moment terugkomt op het beginpunt van deze ééndimensionale wandeling is dus in zekere zin oneindig groot.
Het feit dat de bovenstaande uitdrukking divergeert, ligt niet zozeer aan de factor √π als wel aan de factor √n, die maar betrekkelijk langzaam groeit. Het soortgelijke probleem in twee dimensies, zoals de willekeurige wandeling van George Pólya in de onbekende stad mét zijstraten en kruisingen, leidt tot de som
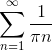
Deze uitdrukking divergeert eveneens, en om dezelfde reden is de kans om in twee dimensies met een willekeurige wandeling thuis te komen in zekere zin oneindig groot.
Als er drie of meer dimensies in het spel zijn, neemt het aantal mogelijkheden echter zo snel af, dat de kans dat je ooit op het beginpunt terugkeert op een zeker moment verwaarloosbaar wordt. De bijbehorende som divergeert namelijk niet meer, maar heeft een eindig antwoord en lijkt op een som als
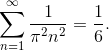
(Een verrassende relatie! Je kunt zelf met de rekenmachine of computer wat termen optellen om te zien hoe snel het antwoord aan de rechterkant benaderd wordt.) In tegenstelling tot de vorige twee sommen groeit de noemer nu zo snel dat deze oneindige hoeveelheid termen toch tot een eindig totaal optellen. De netto kans dat je met een driedimensionale toevalswandeling thuiskomt, is daardoor klein. Een vogel die de weg naar het zonnige zuiden kwijt is, kan dus beter maar niet de strategie van Pólya volgen!
De échte kans op een veilige terugkomst
De redenering die hierboven opgevoerd wordt, is nog niet helemaal volledig. Strikt genomen hebben we geen kans uitgerekend. Kansen kunnen nooit groter zijn dan 1 (oftewel 100%) en al zeker niet divergeren. Dit komt doordat we te veel mogelijke paden meetellen: in de bovenstaande uitdrukking voor qn wordt er geen rekening mee gehouden dat zulke toevalswandelingen al eerder dan na 2n stappen thuis kunnen komen. Als we deze mogelijkheden zorgvuldig opsplitsen, blijkt dat de kans p dat we op een zeker moment terugkeren gelijk is aan
![]()
Hierin is q het resultaat dat we eerder hebben uitgerekend. Zoals we net zagen divergeert q in één en twee dimensies, dus de kans op terugkomst gaat naar honderd procent. Voor meer informatie kun je deze recente samenvatting van Pólya’s ontdekking bekijken.
Toevalswandelingen spelen een belangrijke rol in allerlei processen in de natuur, zoals de Brownse beweging. Bovendien is de thermodynamische beschrijving van gassen nauw verbonden aan het idee dat de beweging van de individuele atomen van een gas als willekeurig beschouwd kunnen worden. Uit dat perspectief bezien is het niet zo gek dat een toevalswandeling in drie dimensies meestal ver van zijn beginpunt verwijderd geraakt. Het is maar goed dat bijvoorbeeld de lucht die in de buurt van je radiator wordt opgewarmd daar niet voor altijd blijft hangen!
