Afbeelding 1. Het casino van Monte Carlo.Naar dit bekende casino is een rekenmethode genoemd die in veel computerexperimenten gebruikt wordt. Foto: Wikipedia-gebruiker Fruitpunchline.
Een formule is nog geen oplossing
Veel theoretisch natuurkundigen proberen dagelijks om nieuwe en betere formules te bedenken om de wereld om ons heen te kunnen beschrijven. Voor veel problemen zijn de juiste formules echter al eeuwenlang bekend. De krachten die op een brug werken als er auto’s overheen rijden, worden bijvoorbeeld prima beschreven door de wetten van Newton. Het feit dat we de juiste formules kennen, betekent echter niet niet dat die formules ook makkelijk op te lossen zijn.
Dat oplossen wordt nog moeilijker als de nauwkeurigheid van het antwoord van groot belang is. Zo is het enorm ingewikkeld om uit te rekenen hoe sterk een brug precies moet zijn om ook in een extreme storm niet in te storten. Zulke problemen, waarbij de juiste formules bekend zijn maar het simpelweg te veel werk is om ze met de hand op te lossen, lenen zich bij uitstek om met een computer aangepakt te worden.
Hoe bereken je π?
Laten we een simpel voorbeeld bekijken van het type experimenten dat met een computer gedaan kan worden. Zoals je misschien wel weet bepaalt het getal π de verhouding tussen het kwadraat van de straal van een cirkel en zijn oppervlakte. De waarde van π kan je opzoeken in een tabellenboek of op het internet, maar hoe zou je die waarde zelf kunnen uitrekenen? Stel je voor dat je een vierkant tekent met zijdes van lengte 1. De oppervlakte van dit vierkant is 1.
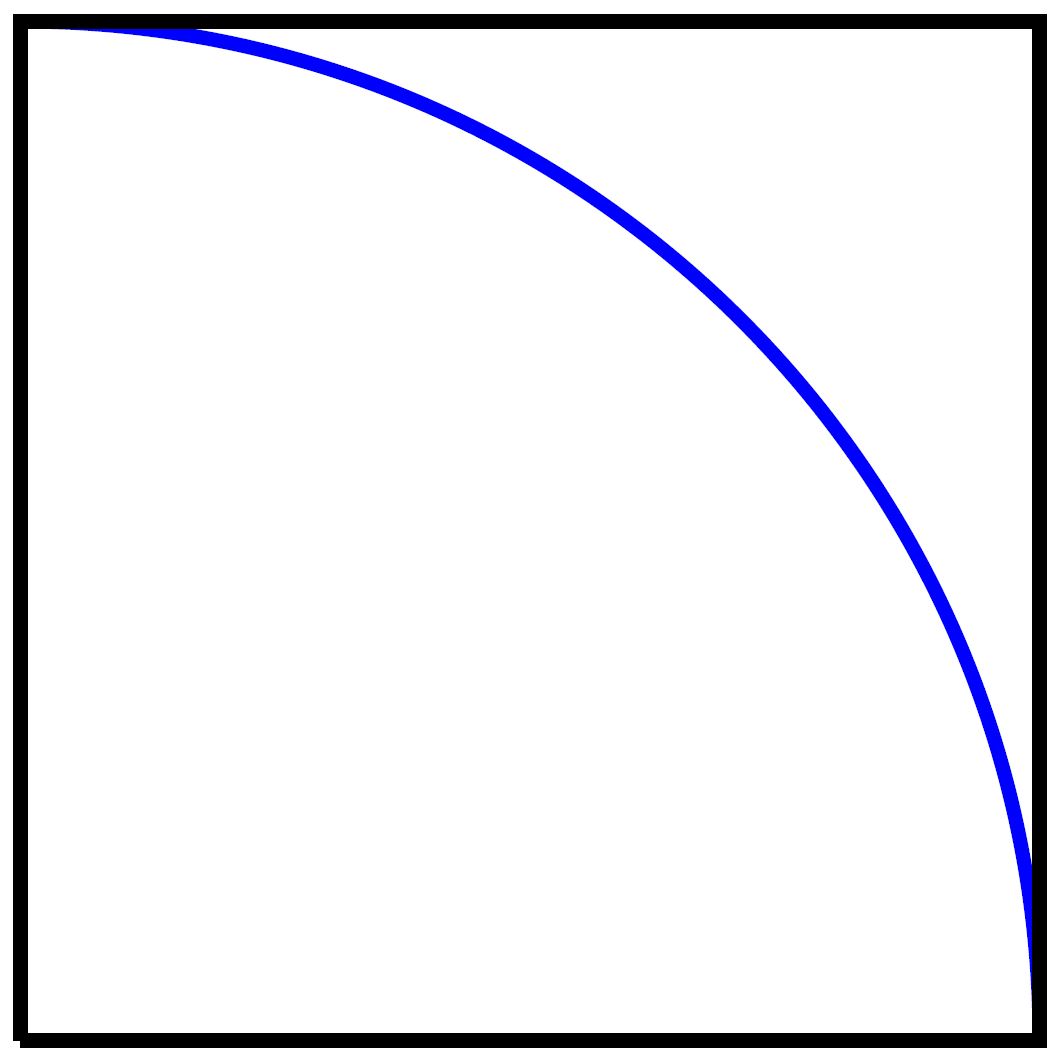
Afbeelding 2. Een vierkant en een kwart cirkel.Als het vierkant oppervlakte 1 heeft, heeft de kwart cirkel oppervlakte π/4. Uit de verhouding van de oppervlaktes kun je dus de waarde van π bepalen.
Teken nu ook een cirkel van straal 1 met de hoek linksonder als middelpunt – zie afbeelding 2 hierboven. De oppervlakte van deze cirkel is precies π, en een kwart daarvan valt binnen het vierkant. De verhouding tussen de oppervlakte van het vierkant en de oppervlakte van de cirkel daarin is dus een kwart van de waarde van π. Door deze verhouding tussen twee oppervlaktes te bepalen, kunnen we dus de waarde van π bepalen. Eén methode om dat te doen wordt ook wel de ‘Monte Carlo’-methode genoemd.
De Monte Carlo-methode
Met pen en papier kun je het volgende experiment gemakkelijk uitvoeren. Doe je ogen dicht, en prik de pen op willekeurige plaatsen in het papier totdat er tien stippen in het vierkant terecht gekomen zijn. Hiervan tel je hoe veel er binnen de cirkel liggen. Dit getal deel je door tien. Vermenigvuldig het eindresultaat met vier, en je hebt een eerste schatting voor het getal π! Gemiddeld zullen immers π/4 van de stippen die je gezet hebt binnen de cirkel vallen, en de rest erbuiten. Met maar tien punten is deze methode natuurlijk niet heel nauwkeurig. Als er twee van de tien punten buiten de cirkel terecht komen is de schatting (π ≈ 3,2) vrij goed, maar als er toevallig één of drie of meer punten buiten de cirkel vallen, wordt het resultaat al veel slechter.
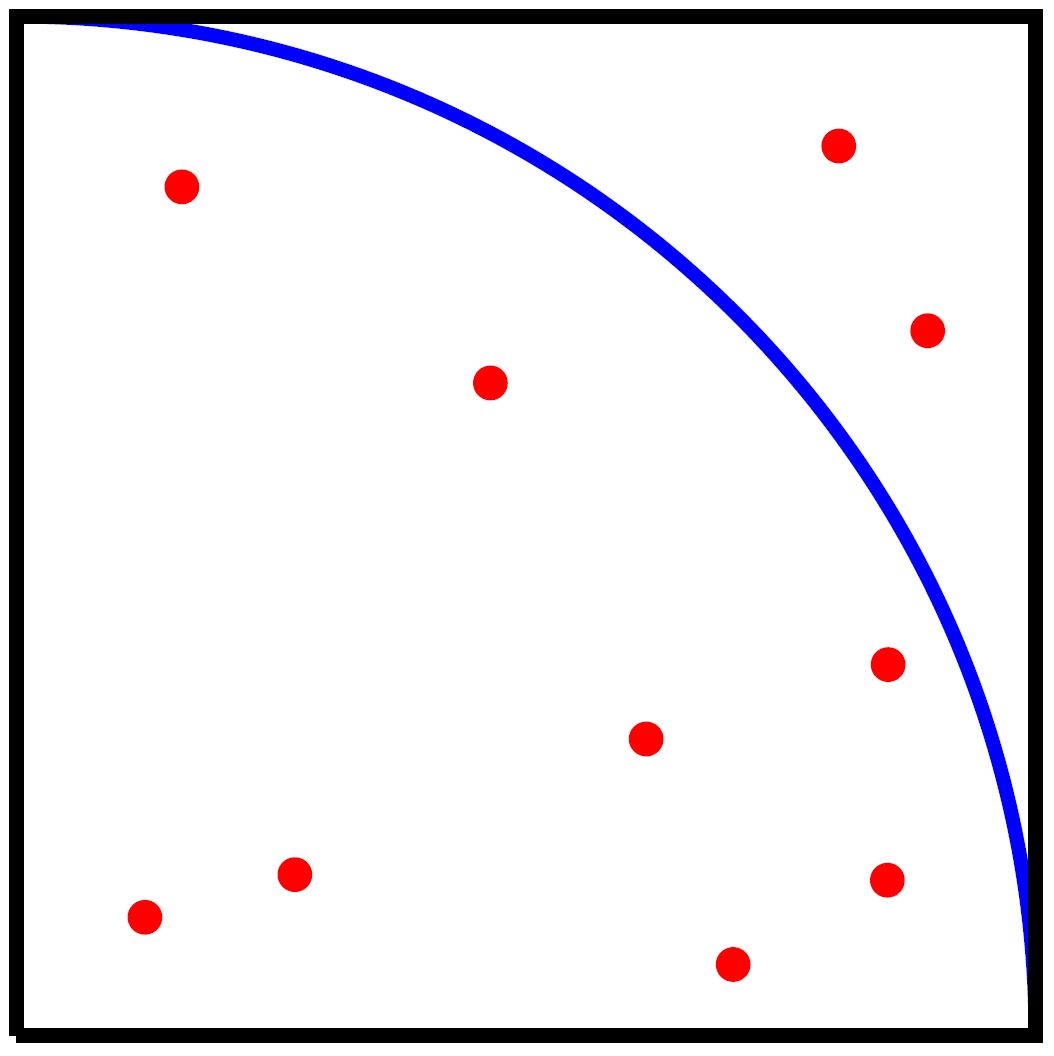
Afbeelding 3. Willekeurige punten in het vierkant.Hierboven vallen acht van de tien willekeurig gezette punten binnen de cirkel. De benadering van π die we zo vinden is dus 4 × (8/10) = 3,2.
Om de schatting beter te maken, zul je meer punten moeten zetten. Je moet dan het bovenstaande experiment dus heel vaak herhalen. Zo lang je maar je ogen dicht houdt, en de punten echt willekeurig over het vierkant verdeeld worden, zal de benadering die je krijgt steeds beter worden. Al met al is deze methode om π te bepalen dus erg eenvoudig, maar kost het natuurlijk ook veel werk en is het flink vermoeiend om dit met de hand uit te voeren.
Computerberekeningen
Eenvoudig maar langdradig en traag werk, is echter precies het soort werk waar computers goed in zijn! Zelfs met de simpelste huis-tuin-en-keukencomputer kun je het bovenstaande experiment in een paar seconden uitvoeren met miljoenen punten. Hierdoor wordt het heel eenvoudig om een goede schatting van π te krijgen.
Alleen: hoe vertel je een computer om zijn ogen dicht te doen? Voor ons experiment is het heel belangrijk dat de punten op willekeurige plekken in het vierkant terecht komen. Als er bijvoorbeeld vaker punten rechtsboven dan linksonder geplaatst worden, vind je uiteindelijk een te kleine waarde van π. De posities van de punten, weergegeven door getallen die de computer “kiest”, moeten willekeurig zijn om het experiment te laten werken. Een computer kan echter alleen maar vast omlijnde recepten volgen, dus hoe krijg je die computer zo ver dat hij willekeurige getallen bedenkt?
Het bepalen van een serie “zo willekeurig mogelijke getallen”, is een fundamenteel probleem in de computerwetenschap dat bijvoorbeeld ook gevolgen heeft voor de beveiliging van computers. Als een website een nieuw wachtwoord voor je bedenkt, is het natuurlijk belangrijk dat dit wachtwoord niet makkelijk te voorspellen is. Veel computers lossen dit probleem op door bijvoorbeeld te luisteren naar ruis op internet, of door willekeurige bewegingen met de muis om te zetten in getallen. Nog mooiere oplossingen gebruiken bijvoorbeeld radioactief verval van deeltjes, wat ook met willekeurige intervallen gebeurt.
Pseudo-willekeurige getallen
Het is natuurlijk niet zo handig om naast elke natuurkundige die een computerexperiment wil doen een radioactieve bron neer te zetten. Bovendien is het voor veel experimenten ook niet zo nodig dat de getallen echt willekeurig zijn, zo lang dat binnen de nauwkeurigheid van de berekening maar zo lijkt. Vaak gebruiken mensen zogenaamde pseudo-willekeurige getallen, die aan de hand van één enkel écht willekeurig getal worden opgebouwd. De radioactieve bron, de ruis van het internet of de muis van de gebruiker geven je een willekeurig getal, en het experiment wordt vervolgens gedaan met de pseudo-willekeurige getallen die je daaruit opbouwt.

Afbeelding 4. John von Neumann.Foto: Los Alamos National Laboratory.
Voor het genereren van die vervolg-getallen bedacht de Hongaarse wetenschapper John von Neumann een mooie methode. Stel dat je begint met een getal met twee cijfers, zoals 42. Kwadrateer dit en neem de middelste cijfers van het kwadraat. Voor dit voorbeeld krijg je 1764, wat leidt tot 76. Het kwadraat daarvan is 5776, dus het volgende getal is 77, enzovoort.
In de meeste gevallen begint de rij getallen die je zo krijgt redelijk willekeurig; als je de twee cijfers bijvoorbeeld gebruikt als coördinaten in een vlak zul je zo een heel aardige benadering van π vinden . Op een zeker moment komen er echter altijd regelmatigheden in zulke rijen – probeer het maar eens uit met het bovenstaande voorbeeld. Er bestaan daarom nog meer verfijnde methodes om uit een kleine hoeveelheid willekeurige data een grote hoeveelheid ‘haast willekeurige’ data te genereren, waarbij het probleem van regelmaat zich pas na héél veel getallen voordoet. Dank zij zulke trucs is het tegenwoordig heel goed mogelijk om “bijna random getallen” te genereren en zo wetenschappelijke experimenten met computers te doen.
