Wat is de snelste glijbaan?

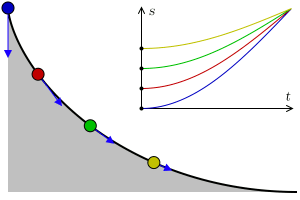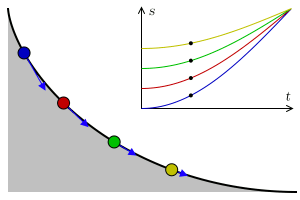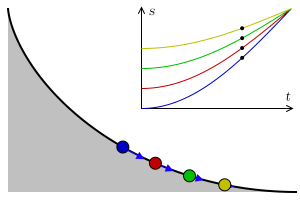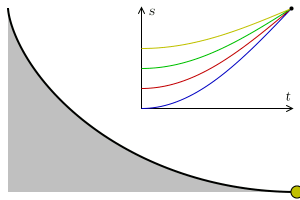
Laten we met het laatste probleem beginnen. Je kunt dat als volgt anders formuleren: hoe ziet de curve eruit die een door de zwaartekracht vallend object neemt zodat dat object het snelst van punt A naar punt B beweegt? We negeren hierbij eventuele wrijving met de helling en met de lucht – denk dus maar aan een waterglijbaan. Het antwoord is niet een rechte lijn; dat is het kortste pad, niet het snelste. Het blijkt voordelig te zijn om het pad langer te maken, door het iets naar beneden te buigen, zodat het object om te beginnen van een steilere helling naar beneden schuift, en de snelheid zo dus sneller toeneemt dan bij beweging langs de rechte lijn – zie ook afbeelding 2. De vraag is dus welke curve deze twee effecten – een korte weg en een grote gemiddelde snelheid – perfect balanceert. Dat wordt ook wel het probleem van de brachistochroon genoemd – van het Griekse brachistos voor kort, en chronos voor tijd.

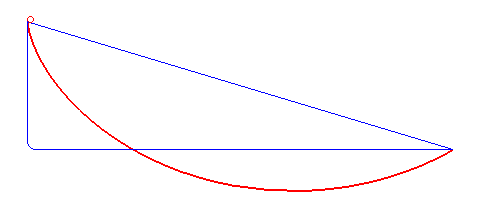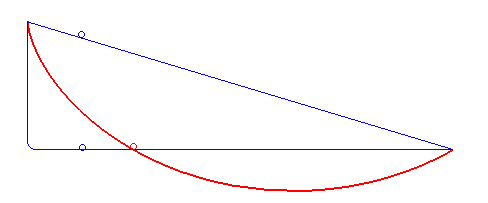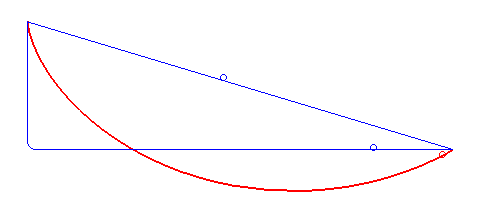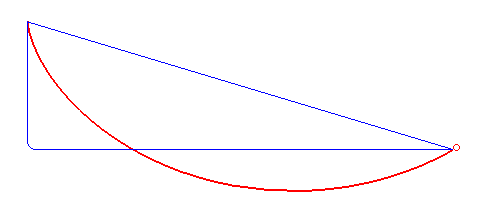
Een van de eersten die een poging deed dit probleem op te lossen was Galileo Galilei, in 1638. Hij dacht dat het snelste pad een deel van een cirkel zou zijn. Het kortste pad blijkt echter een deel van een cycloïde te zijn. Een cycloïde kan gezien worden als het pad dat een punt op een cirkel tekent als je die cirkel over een vlakke lijn laat rollen – zie afbeelding 3. Het is best opmerkelijk dat Galilei dit antwoord niet heeft bedacht, aangezien hij over het algemeen als de ontdekker van de cycloïde wordt beschouwd – hoewel daar tegenwoordig dan weer enige twijfel over is. Wat zeker is, is dat Galilei de naam “cycloïde” heeft verzonnen, en dat hij deze krommen fascinerend vond. Dat is met goede reden, aangezien blijkt dat cycloïdes allerlei bijzondere eigenschappen hebben, en daarom ook wel de ‘Helena van de Geometrie’ worden genoemd, naar Helena van Troje uit het epos Ilias van Homeros. Zo bleek later bijvoorbeeld dat het oppervlak tussen de kromme en de vlakke lijn waarover de cirkel rolt precies drie keer die van de rollende cirkel is, en dat de lengte van het pad nadat de cirkel één keer is rondgedraaid, precies vier keer de diameter van die cirkel is. Verder, zoals ik hieronder bespreek, blijkt de curve de oplossing te zijn voor een aantal interessante vragen, zeker niet alleen het brachistochroonprobleem.

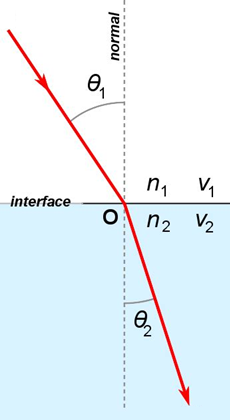
Johann Bernoulli ontdekte de afleiding voor de oplossing van het brachistochroonprobleem in 1696, bijna 60 jaar later. Hij vond de oplossing aan de hand van het principe van Fermat en de daaruit volgende wet van Snellius. Het principe van Fermat zegt dat het pad dat een lichtstraal neemt tussen twee punten, altijd het snelst mogelijke pad is. Zolang de twee punten zich in hetzelfde medium bevinden, is dat een rechte lijn, maar als het licht van één medium naar een ander medium gaat, bijvoorbeeld van lucht naar glas of water, dan leidt het principe van Fermat tot de wet van Snellius. Het licht zal namelijk afbuigen onder een bepaalde hoek wanneer het de overgang maakt, omdat de snelheid van het licht in het ene medium anders is dan in het andere. Dit zal je misschien wel eens opgevallen zijn, bijvoorbeeld bij een paal die in helder genoeg water staat. Een veel gebruikte analogie om dit principe te illustreren is die van een strand met een zee: stel dat je je begeeft in de zee en naar een bepaald punt op het strand wilt komen. Aangenomen dat je sneller loopt dan zwemt, kan het voordelig zijn om, in plaats van recht op je doel af te zwemmen, meer recht op de kust af te zwemmen, zodat je een minder grote afstand hoeft te zwemmen. Je moet dan verder lopen, en de totale afgelegde afstand is groter, maar omdat een groter deel van die afstand gelopen wordt, en je dat sneller kan dan zwemmen, kan dit pad toch sneller zijn. De perfecte afweging van deze effecten om tot het snelste pad te komen, wordt gegeven door de Wet van Snellius – in nette wiskunde uitgeschreven:

\( \frac{\sin\theta_1}{v_1} = \frac{\sin\theta_2}{v_2}  \).

Hierin zijn de \( \theta \)’s de hoeken van inval en uitval van het licht ten opzichte van een loodrechte lijn op het vlak van inslag, en de \(v\)’s de snelheden in de twee verschillende media – zie ook afbeelding 4. De verhouding tussen de sinus van de hoek en de snelheid blijkt dus constant te zijn.

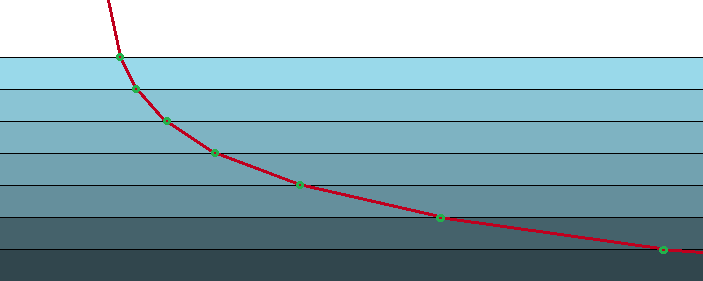
Wat heeft dit allemaal te maken met het brachistochroonprobleem? Zoals uitgelegd geeft de wet van Snellius je het snelste pad. We kunnen het vallende object precies hetzelfde beschouwen. De enige extra stap is dat het object niet op één plek maar op een continue manier zijn snelheid aanpast: het valt immers door de zwaartekracht van de aarde, en een kracht impliceert een versnelling (de tweede wet van Newton). Dit is analoog aan een lichtstraal die beweegt in een medium waarin zijn snelheid op een continue manier verandert naarmate de lichtstraal dieper het materiaal penetreert. Je kan het je voorstellen als een oneindige serie van overgangen zoals in afbeelding 4, die elkaar oneindig snel opvolgen, zoals in afbeelding 5. Aangezien de snelheid van het object zich continu aanpast, zie je aan de wet van Snellius dat de hoek van het object zich ook continu aanpast.

Wat die snelheid op elk punt is, kunnen we afleiden aan de hand van het behoud van energie. Een object in een gravitationeel veld heeft een bepaalde potentiële energie, namelijk \( E_{pot} = mgy\), met \( m \) de massa van het object, \( g \) de versnelling door de zwaartekracht van de aarde, \(g = 9{,}81 m/s^2\) en \( y \) de hoogte ten opzichte van een bepaald nulpunt dat je willekeurig kan kiezen. In ons geval kiezen we dat nulpunt op het beginpunt van het object. Als het object begint te vallen, geldt er behoud van energie, en wordt de potentiële energie omgezet in kinetische energie, \( E_{kin} = \frac{1}{2}m v^2\). Hieruit volgt dus dat

\( mgy = \frac{1}{2} m v^2 \quad \Rightarrow \quad v = \sqrt{2gy}. \)

Dit kunnen we vervolgens invullen in de wet van Snellius, waaruit we krijgen dat

\( \frac{\sin\theta}{\sqrt{y}} = constant\),

en waarin we de constante \( \frac{1}{\sqrt{2g}} \) uit de uitdrukking hebben weggelaten. De kromme die het brachistochroonprobleem oplost moet overal aan deze vergelijking voldoen, oftewel: de sinus van de hoek tussen een verticale lijn en een raaklijn van de kromme moet altijd evenredig zijn met de wortel van de \(y\)-coördinaat ten opzichte van het gekozen nulpunt. Zie afbeelding 6 voor een grafische weergave daarvan.

Toen Bernoulli deze vergelijking zag, herkende hij die als de vergelijking voor een cycloïde, en had hij in feite het probleem opgelost. Om wat historische context te schetsen: Bernoulli beschouwde zichzelf als de beste wiskundige van zijn tijd (beter onder andere dan zijn broer, Jakob Bernoulli, Gottfried Wilhelm Leibniz, en Isaac Newton, die tegen die tijd aan de oude kant was). Het verhaal gaat dat hij zijn dominantie wilde tonen, en daarom het brachsitocroonprobleem publiceerde als uitdaging aan de Europese gemeenschap van wiskundigen. Helaas voor hem bleek dat Newton zijn scherpte nog niet verloren was, en schijnbaar heeft die het probleem in één avond opgelost, met een andere methode, terwijl Bernoulli zelf twee weken nodig had [1]. Newton publiceerde zijn oplossing anoniem, maar Bernoulli schijnt toen hij die oplossing zag gezegd te hebben dat hij ‘de leeuw aan zijn klauwen herkent’. Hoewel dit een populaire anekdote is, schijnt dat Bernoulli echter met ‘leeuw’ niet Newtons status wilde aanduiden, maar dat het een gangbare uitdrukking was: ‘ik herken dit, zoals ik een leeuw aan zijn klauwen herken’. Aan de andere kant schijnt Newton over de uitdaging gezegd te hebben: “I do not love to be dunned [pestered] and teased by foreigners about mathematical things…”.

Hoewel Bernoulli de vergelijking hierboven meteen herkende als de vergelijking voor een cycloïde, kan ik me voorstellen dat voor de lezer niet meteen duidelijk is wat die vergelijking met rollende cirkels te maken heeft. Een mooie afleiding voor deze formule vanuit de beschrijving van de cycloïde die ik gegeven heb, werd gepubliceerd door de Amerikaanse wiskundige Mark Levi [2]. Het is een elegant klein bewijs dat gebruik maakt van een beetje geometrie.

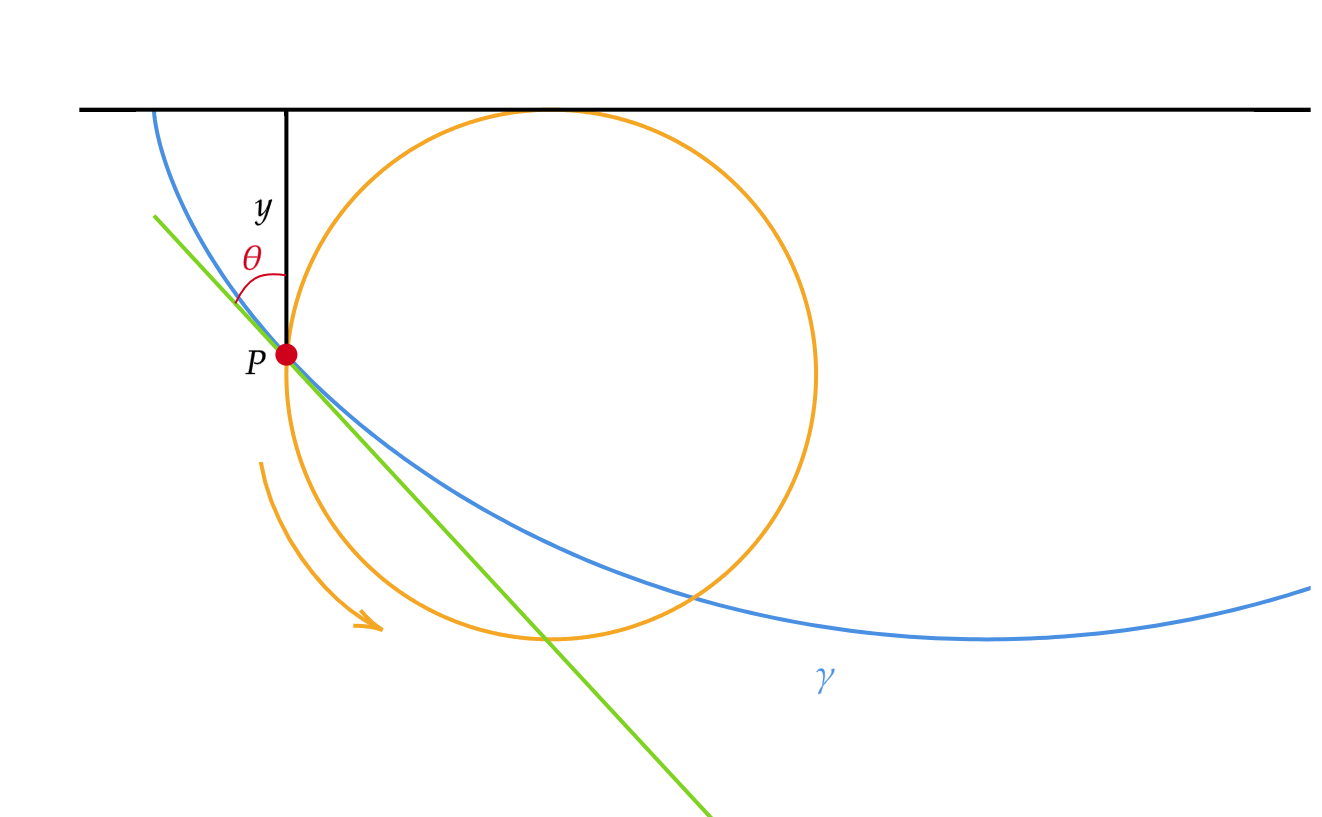
Zoals bij elk geometrieprobleem, beginnen we met het maken van een goede tekening: zie afbeelding 7. Het cruciale inzicht begint met het feit dat, gegeven het punt P op de cirkel waarmee je de curve aan het tekenen bent, het punt C op diezelfde cirkel dat in contact is met de horizontale lijn een instantaan centrum van rotatie vormt voor het punt P: op dat moment draait het punt P heel even rond het punt C. Het gevolg hiervan is dat de raaklijn in punt P van de cirkel waarvan CP de straal is, aangegeven met een bruine stippellijn, dezelfde is als de raaklijn in het punt P van de cycloïde die we aan het tekenen zijn: PC’. Dit betekent op zijn beurt weer dat CP en PC’ een rechte hoek vormen. Door de stelling van Thales betekent dit dat CC’, de schuine zijde van de driehoek CPC’ die zich zo vormt, het midden van de cirkel doorkruist, en dus een diameter is, waarvoor we de letter D gebruiken om de lengte aan te geven.

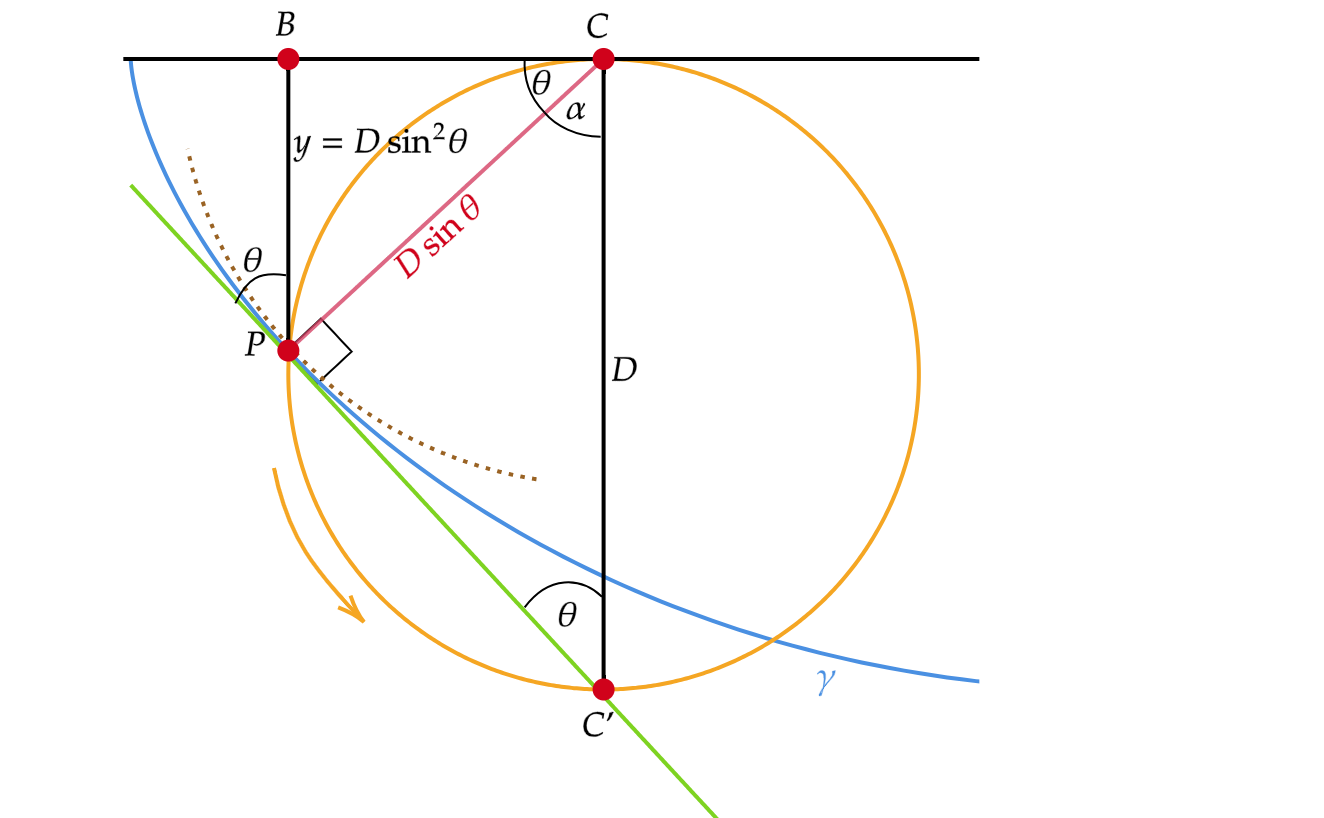
Vervolgens gebruiken we dat de hoek \( \theta \) tussen de raaklijn van de cycloïde in P, en de verticale lijn CC’ (dezelfde hoek die voorkomt in de formule die we hadden gevonden, vanwege F hoeken), ook de hoek is tussen CP en BC. Dit kan je simpelweg zien door je te realiseren dat de hoeken van een driehoek samen 180 graden zijn, dus \( \alpha = 180 – 90 – \theta = 90 – \theta \), en de hoek tussen BC en CP is \( 90 – (90 – \theta) = \theta \). Daarna gebruiken we twee keer de SOS van SOSCASTOA (of SOL van SOLCALTOA, afhankelijk van methode en generatie) om eerst te zien dat de lengte van \( CP = D \sin\theta \), en vervolgens

\( y = D \sin^2\theta \quad \Rightarrow \quad \frac{sin\theta}{\sqrt{y}} = \frac{1}{\sqrt{D}}\).

De diameter \( D \) van de cirkel is constant, dus we hebben nu onze gewilde formule teruggevonden! We zien hiermee dus dat de gevonden formule voor de cycloïde inderdaad de formule is die ook de oplossing geeft voor het brachistochroonprobleem.

Het blijkt, zo ontdekte Christiaan Huygens al eerder, dat de cycloïde niet alleen de oplossing is voor het brachistochroonprobleem, maar ook voor het tautochroonprobleem (Grieks voor zelfde tijd): is er een kromme zodat je vanaf welk punt dan ook op die kromme het vallende gewicht kan laten starten, en de val in alle gevallen even lang duurt? Het antwoord is wederom de cycloïde. Huygens ontdekte dat antwoord terwijl hij de precisie van de penduleklok, die hij heeft uitgevonden, aan het verbeteren was. Een pendule houdt de tijd bij met een gewicht aan een touwtje dat heen en weer slingert. De periode van een slinger is ongeveer constant wanneer je hem met verschillende hoeken ten opzichte van de middellijn laat starten, maar niet helemaal. Als je een pendule langs een cycloïde kan laten vallen, zou het wél precies het geval zijn, en zou de precisie van je klok dus niet afhangen van de hoek waarmee de pendule gestart is.

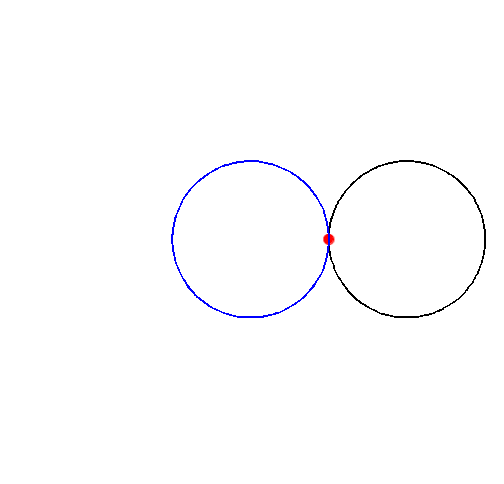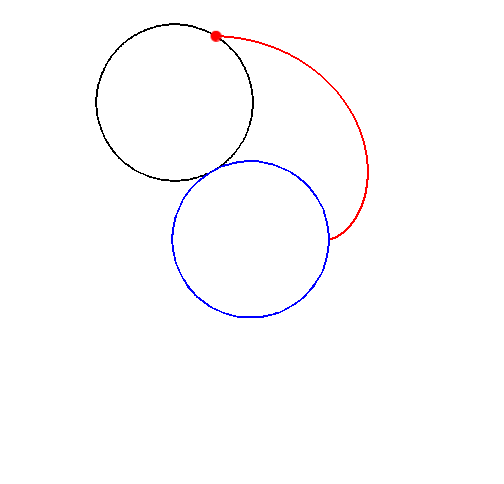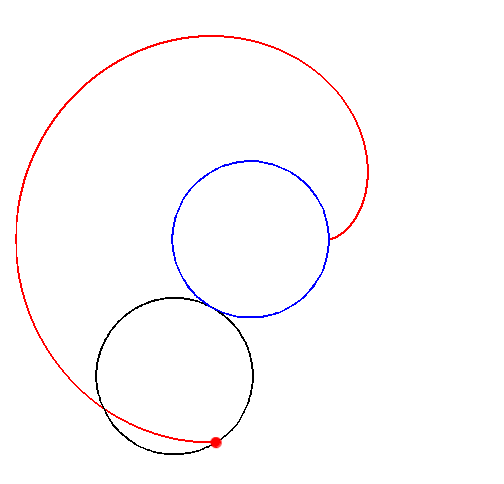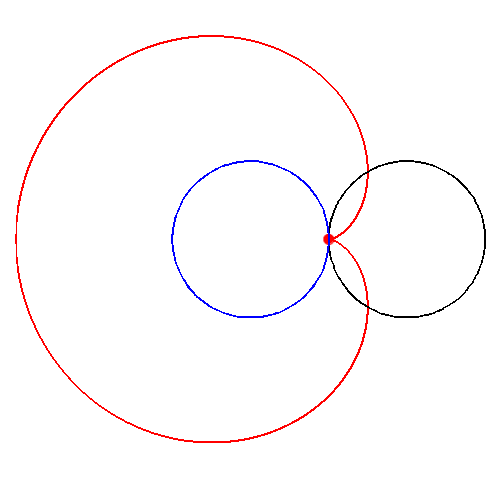
Een andere interessante vorm ontstaat wanneer je de cirkel niet over een vlakke lijn laat rollen, maar over een andere cirkel. De vorm die een punt op de rollende cirkel dan maakt, wordt een epicycloïde genoemd. (Zie hier voor een interessante vraag over deze constructie.) Wanneer de twee cirkels even groot zijn, spreken we specifiek van een cardioïde, vanwege zijn hartachtige vorm (van het Griekse kardia voor ‘hart’) – zie afbeelding 9.

Deze vorm kan je ook hier en daar terugzien. Kijk bijvoorbeeld eens in je koffiekopje, als je boven je een felle lamp hebt. De reflectie van een lichtbron die precies goed op een perfect ronde spiegel valt – hier: de rand van je koffiekopje – resulteert in een cardioïdevorm die op het oppervlak van je koffie wordt geprojecteerd. Als de lichtbron ver weg is, zoals de zon, en recht boven je kopje, krijg je een nefroïde in je kopje koffie, de vorm die je krijgt als de rollende cirkel een straal heeft van de helft van die van de cirkel waar hij overheen rolt. In de praktijk zie je, bij genoeg licht en een voldoende reflecterend kopje, meestal een vorm die ergens tussen de twee in zit. En ten slotte: de centrale vorm die ontstaat in de Mandelbrot-set is ook een cardioïde! Zie afbeelding 10. Zo zijn er nog allerlei andere leuke voorbeelden te vinden waar carioïdes op onverwachte plaatsen voorkomen.

Een leuke video van YouTubekanaal 3blue1brown [1] die je over dit onderwerp kan kijken is de volgende:

Daarnaast is er dit leuke artikel van New Scientist (helaas wel alleen voor abonnees), dat wat van de context en bredere voorbeelden beschrijft.

Voor iedereen is er ten slotte deze leuke video van YouTuber Vsauce, waar hij samen met mythbuster Adam Savage een fysieke cycloïde bouwt en daarmee de verschillende eigenschappen van deze mooie kromme demonstreert:

[1] https://www.youtube.com/watch?v=Cld0p3a43fU

[2] https://www.marklevimath.com/_files/ugd/4d55eb_43090d54f6384c568c2f0f5e116d123f.pdf