Wanneer is meten weten?

Wanneer is meten weten?

Hoe lang ben jij eigenlijk? Dat is eenvoudig te bepalen. Neem een rolmaat, ga tegen de muur staan met een boek op je hoofd en vraag een vriend of vriendin om je lengte af te lezen. Een lastigere vraag is: hoe nauwkeurig is zo’n meting precies? In andere woorden: hoe klein is de foutmarge?

Afbeelding 1. Hoe lang ben je?Zelfs bij het meten van je lengte komen meetfouten kijken. Foto: woodleywonderworks.

Een foutmarge geeft een onder- en bovengrens, waartussen de werkelijke waarde valt die je hebt geprobeerd te meten. In het dagelijks leven kom je daar niet vaak mee in aanraking. De lengte in je paspoort staat immers niet aangeven als 1,62 ± 0,01 meter. En bij het gewicht op een pak pasta vind je geen foutmarge van bijvoorbeeld ±10 gram, terwijl het natuurlijk nooit precies 500g bedraagt. Zelfs de voedingswaarden van de pasta worden niet voorzien van een foutmarge, hoewel daar een heleboel onzekerheid en variatie aan te pas komt. Zo zie je dat we niet gewend zijn om over de nauwkeurigheid van zulke getallen na te denken.

In de wetenschap is het kwantificeren van onzekerheid echter cruciaal. Een groot gedeelte van een experiment bestaat uit het inschatten, doorrekenen en analyseren van foutmarges. Daarbij worden vaak concepten uit de statistiek gebruikt, zoals de bekende standaarddeviatie. In dit stuk beantwoorden we vraag: waarom is foutberekening zo belangrijk en hoe kun je het toepassen, binnen en buiten de wetenschap?

Je gaat hoe dan ook de fout in

Het woord fout klinkt wat negatief, alsof het allemaal de schuld is van de experimentator. Maar vergis je niet, meetfouten zijn onontkoombaar. Het is de taak van de wetenschapper om ze zo klein mogelijk te houden, maar je komt er nooit vanaf. Juist daarom is het zo belangrijk om de fouten bij te houden die bij elke stap het experiment in sluipen. Dat wordt goed geïllustreerd door enkele controversiële ‘ontdekkingen’ die moesten worden teruggetrokken na een nieuwe foutenanalyse. Denk bijvoorbeeld aan de aankondiging in 2011 dat het OPERA-experiment neutrino’s zou hebben waargenomen die sneller dan het licht gingen.

Wat zijn de fouten die komen kijken bij het meten van je lichaamslengte? Om er een aantal te noemen:

• Variatie in je houding: sta je wel helemaal rechtop?
• De hoek van de rolmaat: hangt het meetlint wel recht naar beneden?
• De hoek van het boek op je hoofd: ligt het wel waterpas?

Al deze factoren dragen op hun eigen manier bij aan de totale onzekerheid, en dat is iets wat je meestal kunt uitrekenen. Als de hoek van het boek een foutmarge heeft van ±3 graden, wat is dan het effect op de gemeten lengte? Met een beetje goniometrie kom je daar wel uit. Voor ingewikkeldere experimenten is dit doorrekenen van fouten een hele wetenschap op zich, waar geavanceerde wiskunde aan te pas moet komen.

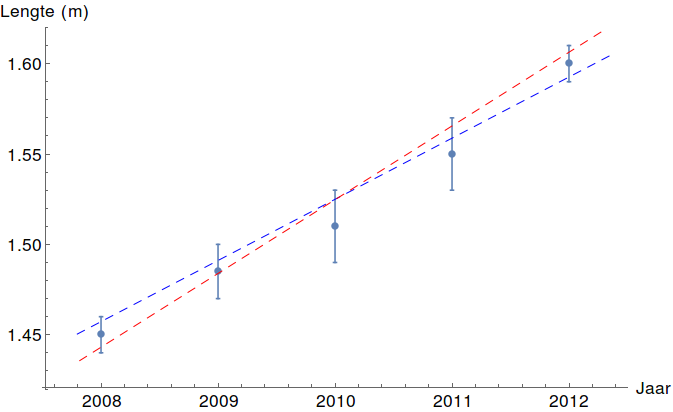
Afbeelding 2. Foutbalken.In een grafiek wordt de onzekerheid meestal aangegeven met foutbalken. Als je vanuit meerdere meetpunten wilt extrapoleren (bijvoorbeeld om te voorspellen hoeveel je volgend jaar zult groeien), moet je daar rekening mee houden. Zowel de rode als de blauwe lijn passen binnen de foutmarges. Zo kun je inschatten hoe nauwkeurig je voorspelling is. Afbeelding van de auteur.

De tweede vraag is hoe je de onzekerheid kunt verkleinen. Natuurlijk kun je nauwkeuriger te werk gaan bij de uitvoering van het experiment. Maar zelfs als je zo zorgvuldig bent als het maar kan, is er altijd nog een andere manier om de foutmarge verder te verkleinen: het experiment herhalen. Elke keer dat je je lengte meet, zullen alle bovengenoemde factoren net iets anders zijn. De ene keer lijk je wat langer, de andere keer wat korter. Door meerdere keren te meten en het gemiddelde te nemen, heffen deze onzekerheden zich gedeeltelijk tegen elkaar op.

Dit kunnen we nog iets preciezer maken. Stel dat je een meting doet met foutmarge ±Δ. Als je dezelfde meting N maal uitvoert, dan wordt de foutmarge op het gemiddelde kleiner met een factor die de wortel van N is: de foutmarge is dan ±Δ /√N. Na vier metingen is de onzekerheid dus de helft kleiner, en na honderd keer heb je een factor 10 verbetering. Dat klinkt misschien als erg veel werk, maar er kleeft een nog groter voordeel aan het herhalen van experimenten: je kunt na afloop een statistische analyse maken van de resultaten. Over het algemeen geeft zo’n analyse een veel duidelijker plaatje van de onzekerheid dan één enkele meting. Om dit te begrijpen moeten we een aantal begrippen uit de kansberekening bespreken.

Ode aan de standaarddeviatie

Als je een meting vaak genoeg herhaalt, zullen de resultaten doorgaans een normaalverdeling (de bekende bell curve) aannemen. Dit is een gevolg van de centrale limietstelling, een prachtig resultaat uit de statistiek. Een normaalverdeling wordt geheel beschreven door twee getallen, het gemiddelde μ en de standaardafwijking σ. De standaardafwijking geeft de spreiding aan van de meetresultaten: na een groot aantal metingen ligt zo’n 68% van de resultaten in het interval tussen μ-σ en μ+σ. Op die manier is de standaardafwijking een heel goede indicatie van de foutmarge van je experiment. Een grotere spreiding betekent meer variatie en dus een grotere foutmarge. Zelfs als je niets weet over de vele onvoorspelbare factoren die bijdragen aan het meetresultaat, kun je zo de mate van onzekerheid bepalen.

Afbeelding 3. Doos van Galton.De doos van Galton is een mooie illustratie van de centrale limietstelling. Waar de balletjes terecht komen wordt bepaald door de som van een groot aantal willekeurige gebeurtenissen: bij ieder pinnetje kan de bal naar links of naar rechts met gelijke kans. Het resultaat vormt een normaalverdeling. De middelste drie kolommen zijn samen net iets meer dan één standaardafwijking breed. Afbeelding: Antoine Taveneaux.

Uit de uitkomst van een experiment wil je als onderzoeker graag conclusies kunnen trekken. Dat het Higgsboson bestaat, bijvoorbeeld. Of dat je nét iets langer bent dan je broer of zus. Maar vanwege de onzekerheid in je meting bestaat de mogelijkheid dat je tot de verkeerde conclusie komt, zoals bij het eerdergenoemde OPERA-experiment. De kans dat dit bij een bepaald experiment gebeurt – dat de meting een conclusie onderbouwt die niet klopt – kan worden berekend aan de hand van de foutenanalyse. Dit heet ook wel de statistische significantie. Deze significantie wordt in de natuurkunde vaak weergegeven als een hoeveelheid standaardafwijkingen.

Zo ging de ontdekking van het Higgsboson gepaard met een significantie van 5σ, wat binnen de deeltjesfysica vaak als een ondergrens wordt gezien om conclusies te mogen trekken. En dat is niet niks: 5σ betekent dat de kans dat deze meting een vergissing was, veroorzaakt door toeval en onzekerheid in de meetapparatuur, kleiner is dan één op de drie miljoen. In andere vakgebieden worden doorgaans lagere grenzen gehanteerd en vaak ook andere maten om de betrouwbaarheid van een resultaat aan te geven, zoals de p-waarde die populairder is in de biologie, economie en sociologie. Maar uiteindelijk komt het allemaal op hetzelfde neer: zonder een scherpe foutenanalyse is een wetenschappelijk experiment weinig waard.