
Het was de theoretisch natuurkundige Philip Warren Anderson die zei: “It is only slightly overstating the case to say that physics is the study of symmetry.” Dat was in 1972, en vandaag de dag is die uitspraak nog onverminderd, of zelfs nog meer, waar.
Wanneer wis- of natuurkundigen over symmetrie praten, bedoelen ze iets algemeners dan de spiegelsymmetrie van bijvoorbeeld een gezicht. Een symmetrie is dan een transformatie (bijvoorbeeld een rotatie, een verschuiving of een spiegeling zoals in het bovenstaande voorbeeld) die je kan doen op je systeem, waarna het systeem op een bepaalde manier onveranderd is. Zo is een gelijkzijdige driehoek symmetrisch onder rotaties van 120 graden (360 gedeeld door 3), en is een cirkel symmetrisch onder alle rotaties rondom zijn middelpunt. We zeggen dat de cirkel een continue symmetrie heeft, aangezien we hem kunnen roteren over elke mogelijke hoek, en we zeggen dat de driehoek een discrete symmetrie heeft, aangezien die vorm alleen symmetrisch is onder rotaties over bepaalde hoeken. Voor sommige groepen van symmetrietransformaties hebben we een naam, omdat ze zo vaak voorkomen. Zo kennen we bijvoorbeeld de Lorentzgroep, vernoemd naar de Nederlandse natuurkundige Hendrik Lorentz. Onder de Lorentzgroep vallen rotaties in de ruimte, zoals een rotatie van de x-as in de richting van de y-as, maar ook een soort ‘rotaties’ tussen de tijdrichting en de ruimtelijke richtingen – die laatste noemen we boosts. Veel natuurkundige wetten die we kennen zijn symmetrisch onder de Lorentzgroep, en dat is geen toeval; eisen dat de natuurwetten symmetrisch zijn onder de Lorentzgroep is hetzelfde als eisen dat ze voldoen aan de wetten van Einsteins speciale relativiteitstheorie. In die theorie is het ‘roteren’ van ruimte en tijd bijvoorbeeld een bekend verschijnsel dat leidt tot tijddilatatie, het langzamer lopen van bewegende klokken.
Eén manier waarop symmetrieën belangrijk zijn in de natuurkunde, is dat ze vaak berekeningen versimpelen die anders moeilijk tot onmogelijk zijn. Zo is bijvoorbeeld het waterstofatoom een van de weinige fysische systemen die we met de quantummechanische Schrödingervergelijking exact kunnen oplossen – dat wil zeggen: waarvoor we de exacte toegestane energieniveaus kunnen vinden van het elektron dat om de kern heen beweegt. Dat dit kan, komt doordat het systeem symmetrisch is onder rotaties. Daarnaast is er nog een subtielere consequentie van symmetrieën: behoudswetten. Volgens Noether’s theorema volgt uit elke continue symmetrie een natuurkundige behoudswet. Zo zorgt symmetrie onder verschuivingen in de tijd voor energiebehoud, en symmetrie onder verschuivingen in de ruimte voor impulsbehoud. Symmetrie onder rotaties zorgt voor behoud van draai-impuls.
Spontane symmetriebreking
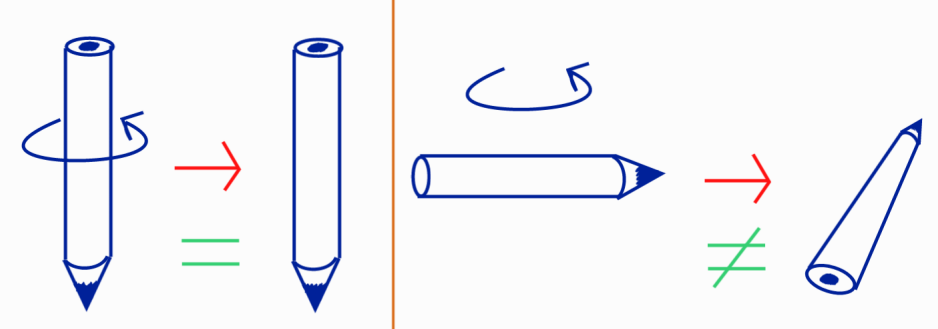
Misschien nog wel belangrijker dan symmetrieën zelf, zijn gevallen waar symmetrieën gebroken zijn, waarbij een systeem op een bepaalde manier niet meer symmetrisch is onder een bepaalde transformatie. Een bekend voorbeeld kom je tegen wanneer je een potlood wil balanceren op zijn punt. De symmetrische toestand is in dit geval het potlood dat op zijn punt balanceert, zoals links in afbeelding 2. Je kan het potlood dan namelijk om zijn as heen draaien, en aangenomen dat je een perfect rond potlood hebt verandert dat niets aan de situatie.
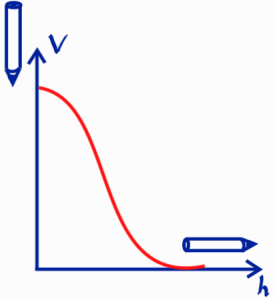
Een scherp geslepen potlood zal echter niet lang op zijn punt blijven staan, maar omvallen. Natuurkundigen zeggen dan dat het balancerende potlood niet in een stabiele toestand is. Het is zoals een bal boven op een steile heuvel leggen. In principe kan je de bal daar neerleggen; aan de bovenkant is de heuvel namelijk vlak en is er dus geen helling. Er is dus geen reden voor de bal om in beweging te komen. Bij de minste verstoring, zoals een klein briesje of een imperfecte plaatsing van de bal, zal de bal echter van de helling afrollen. Dezelfde situatie is voor het potlood afgebeeld in afbeelding 3.
De nieuwe toestand waarin het potlood uiteindelijk verkeert, liggend op je tafel, is niet meer symmetrisch onder dezelfde rotatie waaronder het balancerende potlood symmetrisch was – zie de rechterkant van afbeelding 2. Deze rotatie symmetrie is dus gebroken in de lagere energietoestand van het liggende potlood.
Dit klinkt misschien als een flauw voorbeeld, en je vraagt je misschien af waarom het bovenstaande allemaal relevant is. De reden is dat het begrip symmetriebreking veel meer dan alleen dit eenvoudige voorbeeld beschrijft. Een interessanter voorbeeld is het universum. De wetten die (voor zover we weten) ons universum beschrijven, zijn invariant onder allerlei symmetrieën. Eén zo’n symmetrie is verschuivingssymmetrie; elektromagnetisme, zwaartekracht, of elk ander natuurkundig verschijnsel, werkt hier op dezelfde manier als 50 lichtjaar verderop. De toestand van het universum zélf is echter niet hetzelfde als je alles 50 lichtjaar opschuift. Zo is hier bijvoorbeeld een mooie blauwe planeet, terwijl 50 lichtjaar verderop waarschijnlijk lege ruimte is. Het universum is dus in een toestand van gebroken symmetrie ten opzichte van de symmetrieën van de wetten die het universum beschrijven. Terugkijkend naar afbeelding 3, zou de potentiële energie van het universum door een soortgelijke maar veel ingewikkelder uitziende functie beschreven worden, met meerdere dalletjes, of minima, waar het huidige universum zich in één van die minimale energietoestanden bevindt. Zo’n energielandschap heeft allerlei verstrekkende gevolgen. Zo zou er volgens de quantummechanica een (extreem kleine) kans bestaan dat de toestand van het universum van één minimum naar een ander minimum quantum-tunnelt. Dat zou dan spontaan en op een onvoorspelbaar moment gebeuren, en het universum in die andere toestand zou er totaal anders uit kunnen zien dan het universum waarin we nu leven. Dit is (in theorie) dan ook een soort doomsday, waarvan we de dag niet kunnen voorspellen.
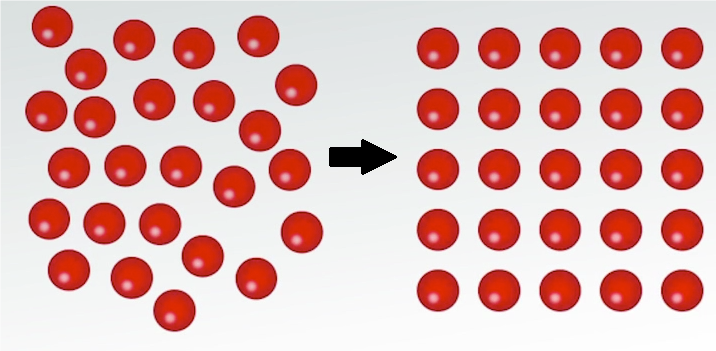
Om weer terug te komen bij de wat meer alledaagse voorbeelden: symmetriebreking beschrijft ook hoe faseovergangen tussen bijvoorbeeld een vloeistof en een vaste stof werken, gebruikmakend van zogenaamde Landautheorie – zie bijvoorbeeld hier of hier voor artikelen over dat onderwerp. Zoals al eerder op deze site besproken is, kan je je een vloeistof voorstellen als een chaotische verzameling deeltjes die door elkaar heen bewegen, zoals links weergegeven in afbeelding 4. Er is hier een continue verschuivingssymmetrie: overal in de vloeistof vind je een ongeordende toestand. Als de temperatuur echter afneemt, dan beginnen de deeltjes zich in een kristalstructuur te rangschikken. Een deel van de symmetrie wordt nu gebroken; het systeem is alleen nog invariant onder discrete verschuivingen over bepaalde afstanden. De overgang van vloeibaar naar vast is een simpel voorbeeld van een faseovergang, maar er zijn uiteraard meer ingewikkelde voorbeelden. Meer algemeen bepalen de symmetrieën van een toestand voor een groot deel wat een bepaalde fase is, en bepaalt de manier waarop die symmetrie gebroken wordt voor een groot deel wat voor type faseovergang er plaatsvindt.
Om een laatste voorbeeld te noemen: magneten! Klassiek gezien kan je je een magneet weer voorstellen als een kristalstructuur, ditmaal van elektronen, waar elk elektron zich op een roosterpunt bevindt. Je kan je het elektron voorstellen als een balletje met een elektrische stroom die rondjes draait om het oppervlak van dat bolletje. Equivalent hieraan kan je je het elektron als een geladen balletje voorstellen dat om zijn as rondtollt. Een lading die in een cirkel beweegt, veroorzaakt een zogenaamd dipoolmoment: alle elektronen in het materiaal worden kleine magneetjes. Dit is een versimpelde manier om de spin van een elektron te beschrijven, die voor onze beschrijving van een magneet volstaat.
De gehele magneet kan je je daarmee voorstellen als een rooster met op elk roosterpunt een pijltje dat een bepaalde kant op wijst, corresponderend met het magneetveld dat daar opgewekt wordt. In een ferromagneet hebben alle nabijgelegen pijltjes de neiging om dezelfde kant op te wijzen; zo ontstaat een toestand met lage energie. De laagste-energietoestand van de hele magneet is er dus een waar álle pijltjes in dezelfde richting wijzen. Als de temperatuur echter hoog genoeg is, en de hele magneet dus meer energie krijgt, wordt het oplijnen van de spins een verwaarloosbaar voordeel en zullen de pijltjes door thermische trillingen van de atomen in allerlei willekeurige richtingen wijzen. Het systeem heeft dan geen voorkeursrichting en is symmetrisch onder rotaties rond meerdere assen. Wanneer de temperatuur weer lager wordt, vindt er een faseovergang plaats en gaan alle pijltjes dezelfde kant op wijzen. Er is dan een netto magnetisatie van het materiaal in een willekeurige richting, en het systeem is alleen nog maar symmetrisch onder rotaties rondom de as van de richting waarin nu alle pijltjes wijzen.
Een interessante consequentie van de bovenstaande symmetriebreking is het ontstaan van zogenaamde Nambu-Goldstone bosonen, vernoemd naar de natuurkundigen Yoshida Nambu en Jeffrey Goldstone. Toevallig was het gisteren 103 jaar geleden dat Yoshida Nambu geboren werd. Het Goldstone-theorema zegt dat, wanneer continue symmetrieën gebroken worden, er massaloze bosonen ontstaan. Bosonen zijn een bepaald soort deeltjes waarover je hier meer kunt lezen; het foton is bijvoorbeeld een boson. Zo ontstaan in het bovenstaande voorbeeld van de magneet twee soorten magnonen. Die magnonen zijn eigenlijk geen ‘echte’ deeltjes, maar quasi-deeltjes die de zogenaamde spingolven die door de magneet heen bewegen beschrijven – daarover later meer. In het eerdere voorbeeld van de faseovergang van een vloeistof naar een gas, waarin verschuivingssymmetrie werd gebroken van een continue naar een discrete symmetrie, ontstaat het fonon, een quasi-deeltje dat de voortplanting van geluid door een materiaal beschrijft. Er zijn zo binnen de gecondenseerde materie (de studie van materialen) heel veel quasi-deeltjes die ontstaan bij de breking van verschillende symmetrieën, en sommige daarvan kunnen best rare eigenschappen hebben!
Als je de voorbeelden hierboven allemaal nogal ingewikkeld vond: maak je niet druk, ik ga het nu hebben over een voorbeeld in de veldentheorie waarin we het ontstaan van Nambu-Goldstonebosonen iets beter kunnen begrijpen.
Nambu-Goldstonebosonen
Veldentheorie bestudeert, zoals de naam al doet vermoeden, velden. Het simpelste voorbeeld van een veld is een scalair veld, een moeilijke term voor wat wiskundigen een ‘functie’ noemen – laten we zeggen \( \phi(x) \). Bij een (reëel) scalair veld kan je je voorstellen dat je aan elk punt x in de ruimte een bepaald getal \( \phi(x) \) toekent. Een voorbeeld is een temperatuurkaart, waar elke plaats op de kaart een temperatuur heeft. Je kan daarnaast ook zogeheten vectorvelden hebben, zoals een elektrisch of magnetisch veld, waar je aan elke plaats in de ruimte niet alleen een getal maar ook een richting toekent. Dit kan je je voorstellen als het ‘vastmaken van een pijltje’ op elke plaats in de ruimte. In het geval van een elektrisch veld beschrijft de lengte van een pijltje op een bepaalde plaats bijvoorbeeld de grootte van de kracht die het elektrische veld uitoefent op een bepaalde lading op die plaats, en de richting van het pijltje wijst dan in de richting waarin die kracht werkt.
Zoals gezegd stelt het Nambu-Goldstone theorema dat er, wanneer een continue symmetrie gebroken wordt, een massaloos deeltje ontstaat – een boson, om precies te zijn. Een simpel voorbeeld hiervan is goed te zien bij de zogenaamde Mexicaanse-hoedpotentiaal. Stel dat we een reël scalair veld \( \phi(x) \) hebben waarvan de potentiële energie beschreven wordt door een functie van de vorm \( V(\phi(x)) = -m^2 \phi(x)^2 + \lambda \phi(x)^4\), met \( m \) een massa en \( \lambda \) een constante. Let op: hoewel het veld \( \phi \) van de plaats x afhangt, hangt de potentiaal \( V \) op zijn beurt alleen af van de grootte van \( \phi \). Voor kleine \( \phi(x) \) draagt de eerste term, een bergparabool als functie van \( \phi \), het meeste bij, en voor grote \( \phi(x) \) draagt de tweede, vierdemachtsterm, het meeste bij. Een vierdemachtsterm ziet eruit als een iets ‘scherpere’ parabool, in dit geval een dalparabool. Onze potentiaal ziet er dus dicht bij \( \phi(x) =0 \) uit als een bergparabool, en verder weg als een dalfunctie, wat samen resulteert in een verloop zoals grofweg geschetst in afbeelding 5.
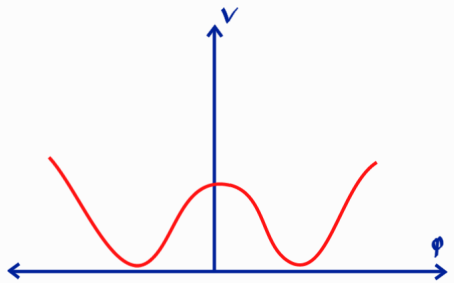
Hier kan je al met enige fantasie een Mexicaanse hoed in zien. Als we nu een extra scalair veld nemen en de potentiaal \( V(\phi_1(x), \phi_2(x)) = -m^2(\phi_1(x)^2 + \phi_2(x)^2) + \lambda (\phi_1(x)^2+\phi_2(x)^2)^2 \) laten zijn, ziet het plaatje eruit zoals in afbeelding 6. Ook met iets minder fantasie moet het nu wel mogelijk zijn hier een Mexicaanse hoed of sombrero in te zien. De vorm wordt overigens ook wel vergeleken met de onderkant van een wijnfles.
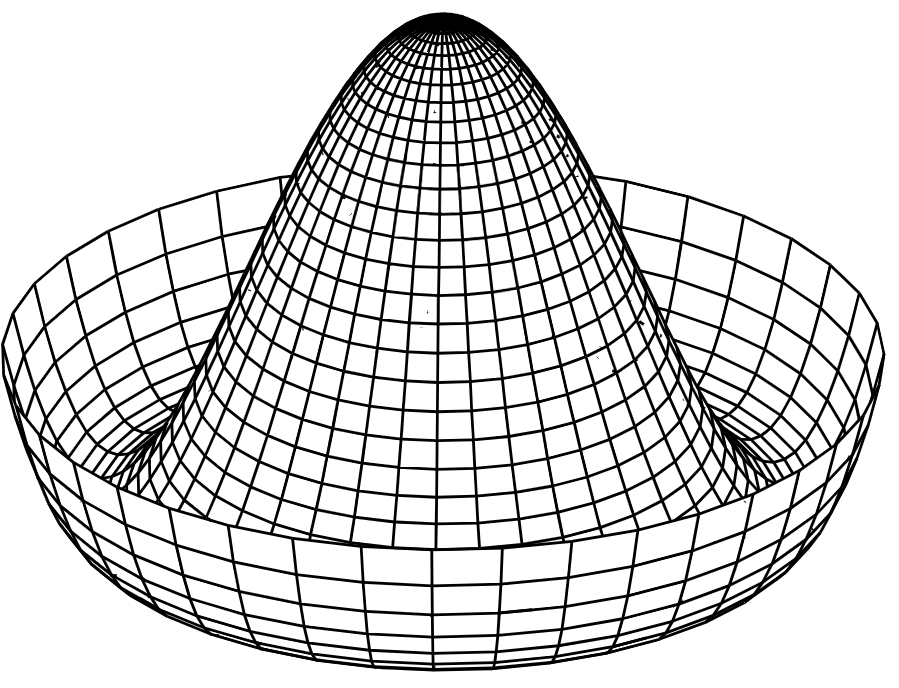
Als de wiskunde in de bovenstaande constructie onduidelijk was, voel je dan vrij om toch gewoon verder te lezen: het punt is dat we een potentiële energie hebben die van de velden afhangt zoals de vorm in afbeelding 6 weergeeft. Het doet je wellicht denken aan de potentiaal die we al in afbeelding 3 hebben gezien in het voorbeeld van het potlood, en dat is geen toeval!
Wat natuurkundigen in quantumveldentheorie doen, is een vacuümtoestand uitzoeken, een toestand van laagste energie dus, en dan de verstoringen rondom dat vacuüm quantiseren. Dat quantiseren betekent dat alleen bepaalde verstoringen toegestaan zijn, en die verstoringen noemen we deeltjes. Zo is een verstoring in een elektronveld een elektron. Bij het voorbeeld van fononen en geluidsgolven die door een vaste stof heen bewegen, geldt iets soortgelijks. Een geluidsgolf is een drukgolf. Zonder geluid is de vaste stof gewoon een rooster met op de roosterpunten atomen. Dit is het ‘vacuüm’ voor het fonon. Een geluidsgolf die door het materiaal beweegt geeft overal waar hij passeert een zetje aan de atomen, die weer het zetje doorgeven aan hun buren. Het quantiseren van zo’n verstoring vertelt ons wat ‘het kleinste beetje geluid’ is dat kan bestaan: het fonondeeltje.
Om de redenering hierboven te laten werken moet je echter wel het juiste vacuüm kiezen. Meestal gaat dat redelijk automatisch en kiezen we simpelweg een vacuüm toestand door te eisen dat alle velden nul zijn: \( \phi_1, \phi_2 = 0 \). Als we echter weer naar de Mexicaanse-hoedpotentiaal in afbeelding 6 kijken, is dat niet een stabiel punt: het is het topje van de berg in het midden. De toestand \( \phi_1, \phi_2 = 0 \) is echter wél de toestand met de meeste symmetrie; je kan de boel draaien om de verticale as, en je systeem blijft onveranderd. We zullen ons vacuüm echter ergens in het stabiele minimum van de ‘geul’ of ‘rand’ van de Mexicaanse hoed moeten kiezen. Het maakt niet uit waar precies in die geul, als je de velden maar zo kiest dat de energie minimaal is. Zo’n toestand is niet meer symmetrisch onder dezelfde rotaties; de rotatie om de verticale symmetrie-as transporteert je langs de geul van de hoed. Al deze opmerkingen kun je één op één terugvertalen naar ons eerdere voorbeeld van het potlood!
Dan komen we nu bij de crux van dit verhaal: waar zijn die Nambu-Goldstonebosonen? Zoals gezegd zijn deeltjes verstoringen ten opzichte van het vacuüm. Als je weer naar de Mexicaanse hoed kijkt, en de vacuümtoestand ‘in de geul’ hebt gekozen, dan kan je twee verschillende verstoringen bedenken: je kan verstoren in de richting van de rand/ de berg in het midden, of je kan verstoren langs de geul van de hoed. In het eerste geval kost het energie om omhoog te gaan in de potentiaal; deze verstoringen geven je daarom massieve deeltjes (want energie = massa; denk aan Einsteins \( E = m c^2 \)). In het tweede geval ga je niet omhoog of omlaag in de potentiaal; deze verstoringen geven je de massaloze Nambu-Goldstonebosonen!
In het volgende deel van dit tweeluik zal ik uitleggen wat een zogenaamde ijksymmetrie is. Spoiler: dat is eigenlijk helemaal geen symmetrie. Technisch gezien gaat het bovenstaande dan ook niet op voor theorieën met zo’n ijksymmetrie, maar we zullen zien dat we kunnen doen alsof onze neus bloedt en het bovenstaande verhaal tóch op die theorieën toepassen. Dan kunnen we daar allemaal mooie natuurkundige fenomenen mee verklaren, zoals de oorsprong van de massa van elektronen en die van de zogeheten W- en Z-bosonen, de dragers zijn van de zwakke kernkracht. Ook kunnen we dan begrijpen waarom het foton geen massa heeft. Ten slotte kan je zien dat de elektromagnetische kracht en zwakke kernkracht, twee van de vier fundamentele krachten, eigenlijk hetzelfde zijn. Dit komt allemaal door het zogenaamde Higgsmechanisme, dat ook nog eens verklaart hoe lage-temperatuursupergeleiders werken. Voldoende moois voor de boeg, dus, maar eerst tijd om even op adem te komen – om achter het antwoord op de vraag in de titel te komen, zal je nog even moeten wachten!