
Quantumcomputers kunnen andere berekeningen uitvoeren dan klassieke computers. Klassieke computers werken met bits, die een waarde van 0 of 1 kunnen aannemen. In de praktijk betekenen die 0 en 1 bijvoorbeeld dat er ergens wél of juist géén elektrische stroom doorheen loopt. Quantumcomputers werken daarentegen met qubits (quantum-bits), die niet alleen maar 0 of 1 kunnen zijn, maar ook een superpositie kunnen vormen en dus “een beetje van beide” kunnen zijn. Het feit dat qubits de regels van de quantummechanica volgen, betekent dat er een ander soort berekeningen mee kan worden uitgevoerd.
In tegenstelling tot wat vaak gedacht wordt, betekent dit niet dat quantumcomputers altijd nuttiger zijn dan ‘normale’ computers. Voor veruit de meeste toepassingen kun je beter een klassieke computer gebruiken, omdat die veel makkelijker zijn om te maken en om mee te werken. Maar bepaalde algoritmes kunnen simpelweg niet worden uitgevoerd door een klassieke computer en wel door een quantumcomputer. Bepaalde problemen kunnen daardoor veel sneller worden uitgevoerd met quantumcomputers dan met gewone computers.
Een bekend voorbeeld daarvan is priemfactorontbinding. Elk geheel getal kan op een unieke manier worden geschreven als een product van priemgetallen: zo is 4 = 2 x 2, 35 = 5 x 7 en 100 = 2 x 2 x 5 x 5. Voor encryptie zijn we meestal geïnteresseerd in getallen die het product zijn van twéé, liefst heel grote, priemgetallen. Voor zulke heel grote getallen is het echter heel lastig om de priemfactoren te berekenen, veel lastiger dan het vermenigvuldigen van die twee priemgetallen tot het grotere getal. Zo is het heel makkelijk (voor een computer, maar ook nog wel voor een mens) om te zien dat 977 x 113 = 110401. Andersom is het voor een computer (en al helemaal voor een mens) relatief moeilijk om te zien dat je 110401 kunt schrijven als 997 x 113. Hoe groter het getal, hoe groter het verschil in moeilijkheidsgraad tussen vermenigvuldigen en ontbinden.
Dit principe wordt bijvoorbeeld toegepast in encryptie, zoals eerder uitgelegd in dit artikel op onze website. Stel je voor dat Alice een geheim bericht wil sturen naar Bob. Zij wil bijvoorbeeld een kluis maken met een bijzonder slot, waar ze dit bericht in kan doen. Om deze kluis op slot te doen, moet je een getal invoeren. De kluis openmaken is echter lastiger: hiervoor moet je de unieke priemontbinding van het ingevoerde getal geven. Nu kan Bob twee van zijn favoriete grote priemgetallen kiezen, zoals 977 en 113, en deze makkelijk met een computer vermenigvuldigen om het getal 110401 te vinden. Dit grote getal geeft hij aan Alice. Dit hoeft niet op een veilige manier te gebeuren: het maakt namelijk niet uit als dit getal onderschept wordt. Alice weet nu hoe ze de kluis op slot moet doen – daarvoor is alleen het grote getal nodig. Vervolgens stuurt ze de kluis naar Bob. Als de priemgetallen die hij gekozen heeft groot genoeg zijn, is het onmogelijk voor buitenstaanders om uit te vogelen dat de kluis opengemaakt moet worden met de getallen 977 en 113. (In de praktijk zal Bob natuurlijk nog véél grotere priemgetallen gebruiken.) Alleen Bob weet de priemfactoren. Zo kunnen Alice en Bob op een redelijk beveiligde manier met elkaar communiceren: niemand anders dan Bob kan de kluis met het bericht makkelijk openen.
Quantumcomputers gooien echter roet in het eten. Er bestaan algoritmes – die alleen op quantumcomputers uitgevoerd kunnen worden – waarmee de priemfactorontbinding een stuk makkelijker wordt. Op dit moment zijn de quantumcomputers hier nog niet krachtig genoeg voor, maar het is een kwestie van tijd voor dat zover is. Daarom zijn mensen op zoek naar nieuwe manieren van encryptie, die niet of moeilijker te kraken zijn, ook niet door quantumcomputers. Eén mogelijke vorm daarvan heet quantum key distribution (QKD). Met een QKD-protocol kunnen Alice en Bob een sleutel met elkaar afspreken en daarbij nagaan of iemand hun sleutel heeft afgeluisterd. Als dit niet het geval is, kunnen ze de sleutel veilig gebruiken, omdat ze zeker weten dat niemand anders ook toegang heeft tot de sleutel.

Afbeelding via Wikimedia Commons
Er zijn verschillende algoritmes die het QKD-proces in de praktijk kunnen brengen. Een voorbeeld hiervan is het BB84-algoritme, dat al in 1984 bedacht werd door Charles Bennett en Gilles Brassard. In dit protocol stuurt Alice één voor één bits naar Bob, die allemaal potentieel deel uitmaken van hun beveiligingssleutel, en achteraf checken ze of die bits zijn afgeluisterd.
De qubits die Alice en Bob gebruiken voor het BB84-algoritme zijn fotonen (lichtdeeltjes), en de waarde van de qubits hangt af van de polarisatie, de richting waarin het licht van elk foton trilt. Daarnaast hangt de gemeten waarde ook af van de richting waarlangs de polarisatie gemeten wordt. Dat werkt als volgt: stel dat Alice een foton maakt dat gepolariseerd is in de verticale richting. Als Bob meet of het foton gepolariseerd is langs de horizontale of verticale as – in de zogenoemde rechtlijnige basis – zal hij met 100% zekerheid meten dat het foton langs de verticale as is gepolariseerd. Maar als hij een andere basis kiest om langs te meten, bijvoorbeeld langs de diagonale as, is zijn meetuitslag plotseling niet met zekerheid bepaald. In dit geval meet hij met een kans van 50% dat het foton schuin naar rechts is gepolariseerd, en met eenzelfde kans van 50% dat het foton schuin naar links is gepolariseerd. Door de eigenschappen van de quantummechanica is het foton na Bobs meting bovendien daadwerkelijk veranderd van polarisatie, in de richting waarin hij die polarisatie gemeten heeft.
Alice stuurt nu een qubit naar Bob, waarbij ze willekeurig een bitwaarde (0 of 1) en een basis (rechtlijnig of diagonaal) kiest. De polarisatie van haar foton wordt aan de hand van deze twee keuzes bepaald. In de rechtlijnige basis correspondeert bitwaarde 0 met een verticale polarisatie en 1 met een horizontale polarisatie. In de diagonale basis hoort 0 bij een polarisatie schuin naar rechts, terwijl 1 dan een polarisatie schuin naar links betekent.

Alice vertelt Bob niet welke bitwaarde en basis ze heeft gebruikt. Bob kiest zelf ook willekeurig een basis en meet de polarisatie van het foton van Alice in deze basis. Mocht hij dezelfde basis hebben gekozen als Alice, dan zal hij ook altijd dezelfde bitwaarde vinden. Als hij de andere basis kiest, dan vindt hij met 50% kans dezelfde bitwaarde en met 50% kans de andere.
Nadat Bob het qubit heeft gemeten, belt hij met Alice. Dit hoeft niet via een beveiligde telefoonlijn te gaan. Ze vertellen elkaar welke basis ze hebben gekozen. Als ze dezelfde basis gebruikten, zullen ze ook dezelfde bitwaarde hebben gevonden. In dit geval slaan ze deze waarde op. Mensen die dit gesprek afluisteren, weten nu alleen welke basis ze hebben gebruikt, niet welke bitwaarde ze hebben gevonden. Als Bob daarentegen een andere basis heeft gebruikt dan Alice, doen ze niets met hun gevonden waarde. Er is dan immers maar een 50% kans dat ze dezelfde waarde voor hun bit hebben afgelezen. Door dit protocol vele malen te herhalen en alleen de “zekere” bits te bewaren, kunnen ze nu een erg lange reeks van overeenkomende bits vormen, waaruit ze hun sleutel kunnen maken. Een voorbeeld van zo’n experiment staat in de tabel hieronder weergegeven. Alleen voor de eerste, derde en zesde bit hebben Alice en Bob dezelfde basis gekozen, dus alleen de waardes die ze hier hebben gevonden voor hun bits slaan ze op voor hun sleutel.
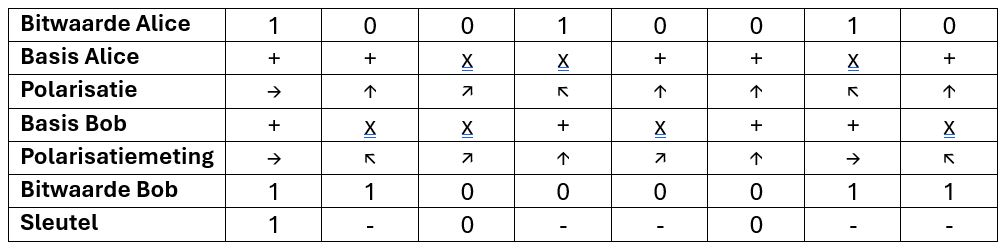
Hoe kunnen Alice en Bob nu nagaan dat niemand hun qubits heeft onderschept en er ook metingen aan heeft gedaan? Hiervoor moeten ze een aantal bits in hun reeks, die in principe perfect overeenkomt, opofferen. Van deze bits vergelijken ze de waardes. Als niemand hun qubits heeft ‘afgeluisterd’, zijn deze allemaal gelijk. Maar wat gebeurt er nu als een derde persoon, Eve, ze heeft proberen af te luisteren?
Eve moet zelf ook een basis hebben gekozen om de qubit in te meten. Als Eve dezelfde basis heeft gekozen als Alice, verandert haar meting niets aan de daadwerkelijke polarisatie van het foton en is haar afluisterpoging niet detecteerbaar. Maar in gemiddeld de helft van de gevallen zal Eve een andere basis kiezen dan Alice. Haar meting verandert hiermee de fysieke polarisatie van het foton. Als Alice het foton verticaal heeft gepolariseerd en Eve kiest de diagonale basis, dan zal het foton nu diagonaal gepolariseerd zijn. Als Bob dan, net als Alice, in de rechtlijnige basis meet, zal hij slechts met 50% zekerheid dezelfde bitwaarde vinden als Alice. Door genoeg van hun reeks aan bits te vergelijken, zullen Alice en Bob dus met grote zekerheid enige onderschepping kunnen detecteren!
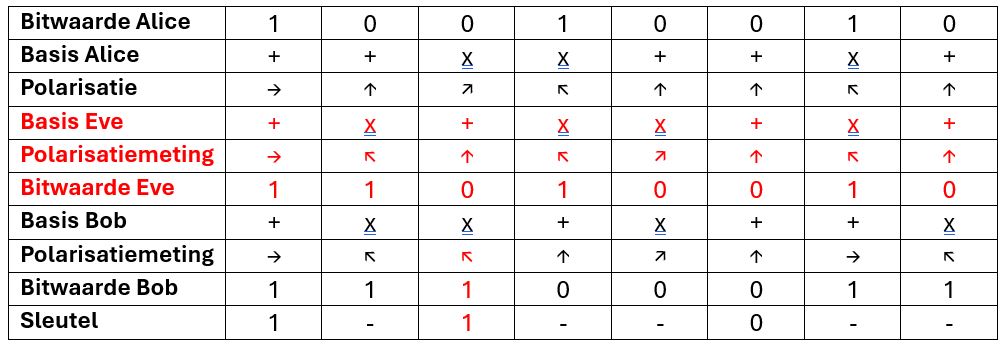
Hierboven staat hoe het experiment van Alice en Bob veranderd zou kunnen worden door de afluisterpoging van Eve. Voor de derde qubit heeft ze een andere basis dan Alice gekozen, waardoor ze de polarisatierichting van het foton heeft veranderd. Bob heeft wél dezelfde basis als Alice gekozen, maar krijgt nu toch maar met 50% kans dezelfde bitwaarde als Alice. Als Alice en Bob deze qubit zouden opofferen om te vergelijken, zouden ze erachter komen dat Eve ze heeft afgeluisterd. Door heel lange reeksen bits te versturen en een groot genoeg aantal bits op te offeren, wordt elke afluisterpoging met grote zekerheid gedetecteerd.
Dit klinkt in theorie heel goed, maar in de praktijk zijn er uiteraard nog vele haken en ogen. Dit protocol gaat ervan uit dat het qubit niet door externe factoren (behalve afluisteraars) verstoord wordt. In de praktijk zal er natuurlijk altijd wel wat “ruis op de lijn” zijn, ook als er géén afluisteraars zijn. Er is nog een nadeel. Eve zou het kanaal expres kunnen verstoren en ervoor kunnen zorgen dat Alice en Bob elke keer tot de conclusie komen dat iemand ze heeft afgeluisterd. Dit zorgt ervoor dat Eve niet kan horen wat voor geheime informatie Alice aan Bob zou willen geven, maar ook Bob krijgt de informatie zo nooit te horen! Daarnaast heeft niet iedereen altijd een fotonpolarisator of polarisatiemeter in zijn achterzak zitten. Hoe dan ook: voor communicatie die echt heel veilig moet gebeuren, bijvoorbeeld voor het doorgeven van gevoelige informatie tussen overheden, zou je wel een protocol zoals ik hier heb beschreven kunnen gebruiken. Quantum key distribution wordt ook al daadwerkelijk, al is het nog op kleine schaal, toegepast!
In principe zou men met deze algoritmes dus vrijwel zeker kunnen weten of iemand heeft afgeluisterd. Daarom wordt er volop in geïnvesteerd en onderzoek naar gedaan, vooral naar hoe dit soort processen kunnen worden opgeschaald. Hier komt het nieuwe onderzoek, waaraan de onderzoekers uit Delft meewerkten, om de hoek kijken! Een groot nadeel aan de weinige quantumcomputers die er zijn, is dat de fysieke implementatie van de qubits vaak verschilt van computer tot computer. Programma’s die geschreven worden voor zo’n quantumcomputer worden heel specifiek geschreven voor de hardware waaruit de computer bestaat. Om grootschalig gebruik te kunnen maken van quantumcomputers willen mensen dit netwerk van verschillende computers met elkaar verbinden. Als elke individuele computer andere software nodig heeft, staat dat opschaling natuurlijk erg in de weg. De wetenschappers die het nieuwe artikel publiceerden, hebben een architectuur gebouwd waarmee dit nu niet meer nodig is. De programmeur kan nu algemene software schrijven die vervolgens toegepast kan worden op verschillende quantumcomputers, met verschillende hardware!
Als quantumencryptie– bijvoorbeeld met quantum key distribution – een realiteit wordt op grotere schaal, zullen er veel quantumcomputers met elkaar verbonden moeten zijn. Als al die quantumcomputers net iets anders werken, hoeven Alice en Bob (en Charlie en David etc.) niet elk afzonderlijk een programma te schrijven speciaal voor hun quantumcomputer, maar hoeft dat maar één keer te gebeuren.
In de ontwikkeling van de gewone computer was standaardisering ook een belangrijke stap in de opschaling van het gebruik en de toegankelijkheid van de systemen. Daarom zijn wetenschappers zo enthousiast over dit onderzoek, dat juist die verbinding tussen verschillende netwerken makkelijker mogelijk maakt.
Voorlopig is deze techniek nog niet beschikbaar voor gewone mensen zoals jij en ik, maar dat was ook ooit zo voor de computer waar ik nu dit verhaal op schrijf. Wie weet wat te toekomst brengt…