
Afbeelding 1. Yoichiro Nambu (1921-2015)Foto: Betsy Devine.
Yoichiro Nambu, die in 2015 op 94-jarige leeftijd overleed, leverde meerdere belangrijke bijdragen aan de moderne theoretische natuurkunde. Zijn naam duikt bijvoorbeeld op in de snaartheorie, waar de Nambu-Goto-actie de beweging van de eenvoudigste snaardeeltjes beschrijft. Ook gaf hij zijn naam aan de zogeheten Nambu-Goldstonebosonen, die in het dagelijks natuurkundig taalgebruik overigens vaak Goldstonebosonen worden genoemd – maar in dit artikel gebruiken we uiteraard de volledige naam! Nambu-Goldstonebosonen zijn massaloze deeltjes die ontstaan als een continue symmetrie spontaan gebroken wordt. Dat is nogal een mondvol termen, dus laten we die een voor een eens wat beter bekijken.
We beginnen met het concept ‘continue symmetrie’. We kennen het begrip symmetrie natuurlijk uit ons dagelijks taalgebruik: een object is symmetrisch als je het bijvoorbeeld kan spiegelen of draaien en het er dan nog steeds hetzelfde uitziet. Dat geldt voor sneeuwvlokken, (ongeveer) voor gezichten, voor een hoelahoep, enzovoort.

Afbeelding 2. Een sneeuwvlok.Een sneeuwvlok ziet er hetzelfde uit als we hem spiegelen of draaien. Foto: Egor Kamelev.
In de natuurkunde spelen symmetrieën een belangrijke rol. Zo zijn symmetrieën gerelateerd aan behouden grootheden, zoals Jasper van Wezel al eens uitlegde. Daarbij gaat het vaak om wat meer algemene symmetrieën dan spiegelen of draaien: bijvoorbeeld om translaties. In het genoemde artikel werd de situatie van een oneindig lang touw beschreven: er is daar geen verschil tussen het rechte touw zoals wij dat hebben neergelegd, en het touw nadat eraan getrokken is (een translatie). Dit is een voorbeeld van een continue symmetrie: het maakt niet uit hoeveel er precies aan het touw getrokken wordt, alle translaties laten de toestand (het touw) ‘invariant’.
Zo’n translatiesymmetrie is ook aanwezig in bijvoorbeeld vloeistoffen. In het linker plaatje van afbeelding 3 zien we een vloeistof: de moleculen bewegen vrijelijk door elkaar heen in willekeurige richtingen. In deze toestand is er volledige translatiesymmetrie: als we met een microscoop naar deze vloeistof kijken, en de vloeistof in willekeurig welke richting willekeurig veel opschuiven onder de microscoop, dan zien we nog steeds eenzelfde, ongeordende toestand.
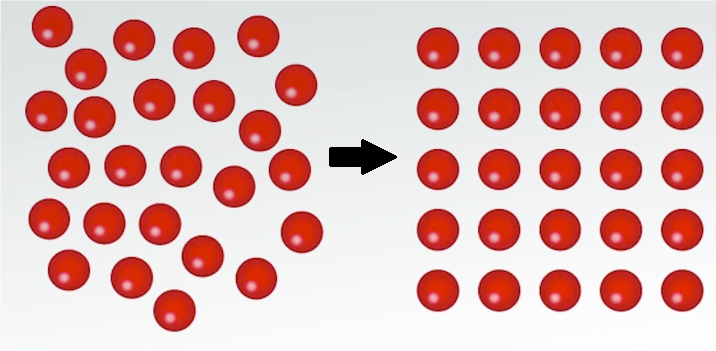
Afbeelding 3. Spontane symmetriebreking.De fase-overgang naar een kristal is een voorbeeld van spontane symmetriebreking. (Bron onbekend.)
Stel nu dat we de vloeistof afkoelen. Onder een zekere temperatuur zal die stollen en (voor bepaalde stoffen) een kristalstructuur aannemen. Deze faseovergang is ook te zien in afbeelding 3. In de rechter toestand is de continue translatiesymmetrie ‘spontaan’ gebroken: als we onze microscoop over een bepaalde vaste afstand in een vaste richting (omhoog of opzij) verplaatsen, zien we weer exact hetzelfde plaatje. De grondtoestand (de toestand met de laagste energie, in dit geval deze kristal-toestand) is niet meer invariant onder alle translaties, maar alleen nog onder discrete translaties. (De linker toestand in de afbeelding is natuurlijk ook niet exact invariant onder translaties, maar alle meetbare natuurkundige eigenschappen van de vloeistof die daar is afgebeeld zijn dat wel.)
Een ander voorbeeld van spontane symmetriebreking is het volgende. Stel dat het je lukt om een potlood op zijn punt te laten balanceren. Deze toestand is volledig symmetrisch: alle richtingen waarin het potlood zou kunnen vallen zijn gelijk. Uiteraard zal het potlood na verloop van tijd (waarschijnlijk behoorlijk snel) omvallen. De symmetrie is dan gebroken – nu is maar één richting belangrijk, die waarin het potlood gevallen is. De toestand is daarmee wel stabieler geworden: het potlood bevindt zich als het plat op tafel ligt in een grondtoestand, een toestand met de laagste energie. Dit is de crux van spontane symmetriebreking: het gaat erom dat een grondtoestand niet langer invariant is onder de (volledige) symmetrie.
Hier komt Nambu in het spel: hij realiseerde zich dat de eigenschappen van de grondtoestand belangrijk zijn bij het bestuderen van spontane symmetriebreking. Stel dat een bepaalde grondtoestand inderdaad niet langer invariant is onder de oorspronkelijke symmetrie, maar wel nog onder een deel daarvan. Bij de faseovergang naar een kristal was de grondtoestand bijvoorbeeld niet meer invariant onder continue translaties, maar wel nog onder discrete translaties. Volgens het Goldstonetheorema leidt een dergelijke symmetriebreking tot het bestaan van massaloze deeltjes (of quasideeltjes), de Nambu-Goldstonebosonen, die je kunt zien als excitaties van de grondtoestand. In het geval van ons kristal zijn dat bijvoorbeeld de zogeheten fononen: trillingen in de uitwijking van de deeltjes in het kristal, die zich als golven verplaatsen (en daarmee overigens verantwoordelijk zijn voor het doorgeven van geluid). Als zo’n golf gelokaliseerd is rond een bepaalde plek gedraagt die zich als een deeltje, maar wel een deeltje ‘zonder traagheid’ – zonder massa, dus.
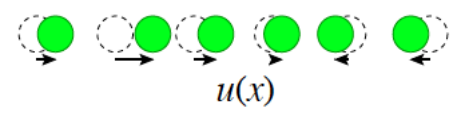
Afbeelding 4. Fononen.Fononen zijn collectieve uitwijkingen van moleculen die zich als golven door een kristal kunnen verplaatsen. (Bron onbekend.)
Het Goldstonetheorema voorspelt ook hoeveel types van dit soort deeltjes er ontstaan. Dat heeft te maken met het verschil tussen de oorspronkelijke symmetrie, en de symmetrie die na breking overblijft. Dat is nogal een wiskundig verhaal, maar met nog een voorbeeld komen we een heel eind. Denk daarvoor aan een ferromagneet: een materiaal dat zelf geen magneetveld opwekt, maar wel reageert op een extern magneetveld – het bekendste voorbeeld is waarschijnlijk ijzer.

Afbeelding 5. Magnetisme.Kompasnaaldjes van ijzer reageren op een extern magneetveld. Afbeelding uit een YouTubevideo van UniServeScienceVideo.
Een ferromagnetisch materiaal kun je beschrijven als een verzameling van allemaal kleine ‘spins’ (een soort kompasnaaldjes). Die spins Si zijn vectoren: ze hebben een grootte en een richting. We schrijven een vetgedrukte S om aan te geven dat de spin een vector is; i labelt de spin, en als we N spins hebben loopt i dus van 1 tot N. In een driedimensionaal object kunnen de spins in elke willekeurige richting wijzen; het materiaal is dus symmetrisch onder draaiingen in drie richtingen. In de wiskunde noemen we een dergelijke structuur een driedimensionale symmetriegroep: je kunt de draaias een willekeurige kant op laten wijzen (twee vrijheidsgraden) en vervolgens een draaiing onder een willekeurige hoek om die as doen (de derde vrijheidsgraad). Een belangrijke eigenschap van het materiaal, die de toestand van alle spins beschrijft, is de magnetisatie, een soort gemiddelde van alle spins van het materiaal:
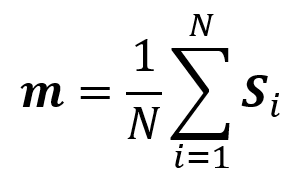
Stel nu dat we het materiaal afkoelen; dit betekent dat er minder energie in het systeem beschikbaar is. Op een gegeven moment is het energetisch voordeliger om alle spins in dezelfde richting te laten wijzen. Hierdoor is de grondtoestand – de toestand met de laagste energie – niet meer invariant onder draaiingen in alle richtingen. Het systeem is nu immers alleen nog symmetrisch onder draaiingen om de as die samenvalt met de richting van de spins. Er treedt dus spontane symmetriebreking op! Die fase wordt beschreven met een ééndimensionale symmetriegroep: er is nog één vrijheidsgraad over. Volgens Goldstone’s theorema moeten we nu in dit voorbeeld kijken naar het verschil in dimensie tussen deze en de oorspronkelijke symmetrie. Dat verschil is twee, en er moeten dus twee massaloze quasideeltjes zijn.
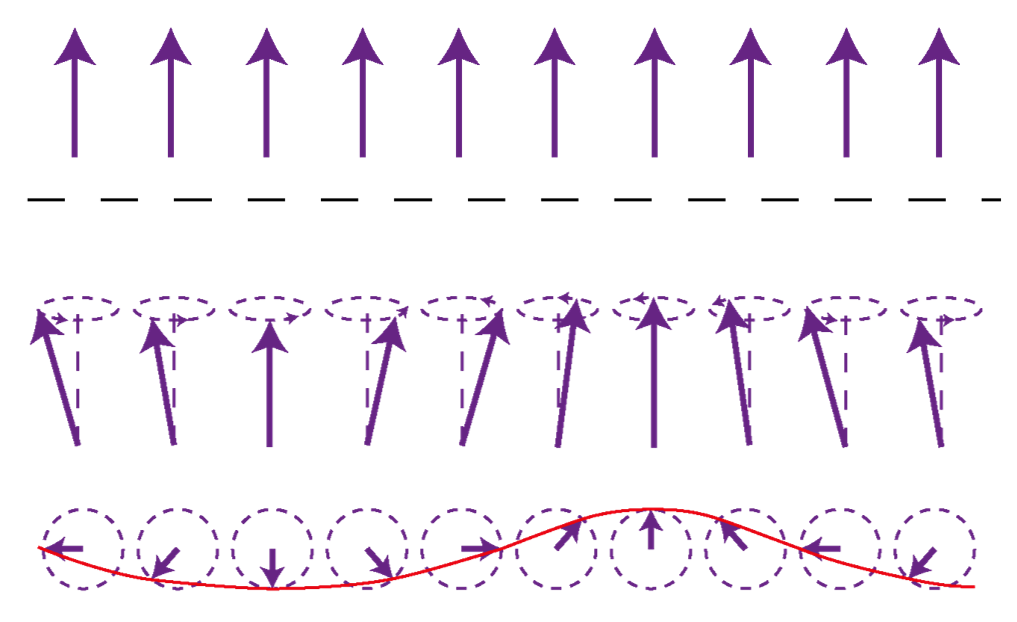
Afbeelding 6. Spingolven.Bovenin zien we de grondtoestand: alle spins wijzen in dezelfde richting. Onderin zien we de spingolven (zij- en bovenaanzicht). Afbeelding: Rijksuniversiteit Groningen.
Die deeltjes moeten we zoeken in de excitaties van de grondtoestand. Laten we de magnetisatie van de grondtoestand µ noemen. We kunnen dan schrijven
m(x) = µ + σ(x)
waar σ(x) de excitaties zijn van de magnetisatie van de grondtoestand – de kleine afwijkingen van de gemiddelde waarde , dus. Op elke plek kan zo’n excitatie in twee richtingen plaatsvinden: de richting van de spin kan immers in twee richtingen een klein beetje bewegen ten opzichte van de gemiddelde waarde. Dergelijke excitaties heten ‘spin-golven’, en daar zijn dus twee types van. Dit zijn onze Nambu-Goldstonebosonen!
Voor zijn werk aan spontane symmetriebreking in het standaardmodel van de elementaire deeltjes ontving Yoichiro Nambu in 2008 de Nobelprijs. Zijn theoretische ontdekkingen waren ook noodzakelijk voor het beschrijven van het Higgs-mechanisme, waar in 2013 de Nobelprijs voor werd toegekend. Ook daar is sprake van een spontane symmetriebreking, maar in dit geval hebben de deeltjes die daarbij ontstaan wél een massa, integendeel tot de massaloze Nambu-Goldstone bosonen die we hierboven beschreven. Dat is een nogal cruciaal aspect: het Higgs-mechanisme geeft massa aan de elementaire deeltjes. Al die onderwerpen zullen we in toekomstige artikelen nog eens beschrijven, maar dit alles laat nog eens zien hoe belangrijk Nambu’s werk voor de moderne theoretische natuurkunde geweest is. Die Nobelprijs was dubbel en dwars verdiend.