
Afbeelding 1. Een knoop.Knopen leiden tot mooie wiskunde – en die wiskunde vervolgens weer tot mooie natuurkunde. Foto: Gabe Popa. (CC BY 2.0)
Je komt bijna dagelijks knopen tegen, bijvoorbeeld bij het strikken van je veters of bij het ontwarren van het snoer van je oordopjes. Het zal je misschien verbazen, maar er is een hele tak van de wiskunde die zich focust op deze knopen: de knopentheorie. In de wiskunde is een knoop gedefinieerd als een gesloten lusje dat – al dan niet in de knoop – in de ruimte zweeft, zoals in afbeelding 2. Wiskundigen zijn al vanaf de 18e eeuw bezig met het beschrijven van de verschillen en overeenkomsten tussen allerlei soorten knopen. De reden dat ik op deze natuurkundige website over dit onderwerp schrijf, is een belangrijke ontdekking van Edward Witten uit de jaren 80. Witten heeft laten zien dat knopen ook een belangrijke rol spelen in de natuurkunde – om specifieker te zijn: in de quantummechanica.
Voordat we het verband met de quantummechanica kunnen zien, zal ik eerst een korte uitleg geven van de belangrijkste aspecten van de knopentheorie die we hier nodig hebben. Jarenlang waren wiskundigen gebrand op het oplossen van het volgende probleem. Als iemand je een heel ingewikkelde knoop geeft, bijvoorbeeld de knoop in afbeelding 2, dan kan je een tijdje proberen om hem te ontwarren. Als dat dan niet lukt, zou je willen concluderen dat het niet mogelijk is, maar misschien heb je het wel niet goed genoeg geprobeerd. Hoe kan je bewijzen dat de knoop niet uit elkaar te halen is?
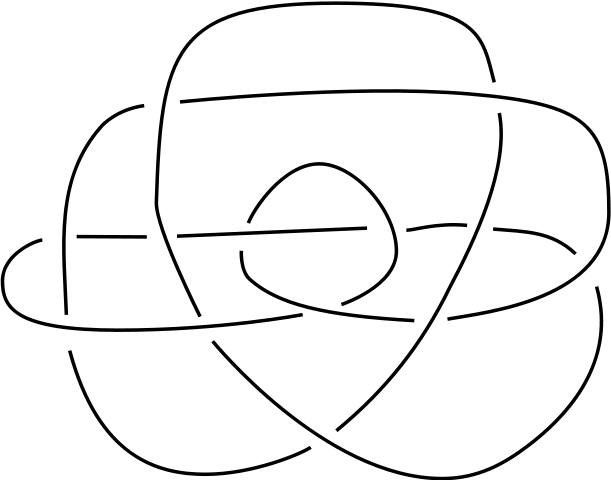
Afbeelding 2. Een wiskundige knoop.Een voorbeeld van een knoop. Kan je deze knoop ontwarren? Bron: Wikipedia. (CC BY-SA 3.0)
Een manier om deze vraag te beantwoorden, is het uitrekenen van een knoopinvariant. De specifieke knoopinvariant waar ik het hier over wil hebben, heet het Jonespolynoom, en is ontdekt door Vaughan Jones in 1984. Het Jonespolynoom is een manier om voor elke knoop K een bijbehorend object JK uit te rekenen. Dat “object” is in dit geval een polynoom: een som van machten van een variabele x, zoals bijvoorbeeld x2 + 3x + 5. Voor knopen die equivalent aan elkaar zijn – wat wil zeggen dat je ze met wat gefrummel in elkaar kan vervormen – is dit polynoom hetzelfde. Bij de “triviale” knoop, het lusje zonder knopen (zie afbeelding 3) hoort ook een heel simpel polynoom: 1. Als je dus een ingewikkelder polynoom, niet gelijk aan 1 vindt, dan weet je zeker dat de knoop niet te ontwarren is! Algemener weet je van alle knopen die niet hetzelfde polynoom krijgen, dat die knopen werkelijk verschillend zijn.
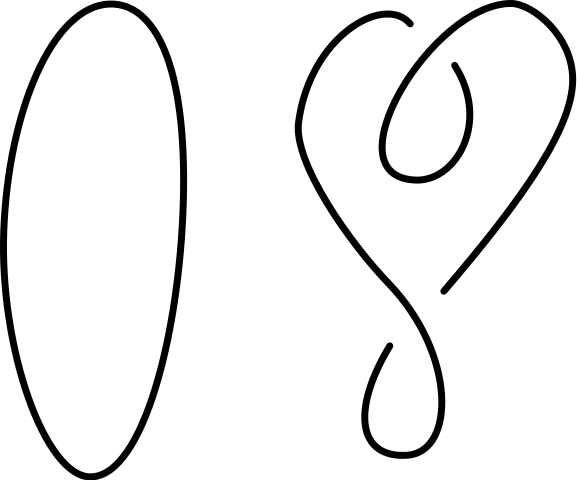
Afbeelding 3. Tweemaal de triviale knoop.Dit zijn twee verschillende, maar equivalente knopen. Zoals je ziet kan je de rechter knoop gemakkelijk in de eerste omvormen. Bron: Wikipedia.
Het mooie van het Jonespolynoom is dat je het voor elke knoop kan uitrekenen, hoe ingewikkeld die ook is, als je maar genoeg geduld hebt, door het volgen van eenvoudig stappenplan. Benieuwd naar hoe je dat doet? Daarover schrijf ik binnenkort een vervolgartikel!
Wat Witten heeft ontdekt, is dat het Jonespolynoom voor een bepaalde knoop ook uit te rekenen is in de quantummechanica. Om dit uit te leggen zal ik kort iets over de quantumtheorie vertellen.
Als een klassiek deeltje, denk bijvoorbeeld aan een voetbal, zich van punt A naar punt B beweegt, zal het dit doen door het pad te volgen dat beschreven wordt door de wetten van Newton. Als je weet welke krachten er op het deeltje werken, kan je dit pad precies uitrekenen. (Zie bovenin afbeelding 4.) In de quantummechanica daarentegen, zou een deeltje elk mogelijk pad tussen de punten A en B kunnen volgen, bijvoorbeeld het pad aangegeven onderin in afbeelding 4. Elk van deze paden heeft een bepaalde kans. De kans dat het deeltje het klassieke pad volgt, is het grootst, maar alle andere paden zijn ook mogelijk. De kans, vaak amplitude genoemd, van een bepaald pad K kan je uitrekenen in de quantummechanica met behulp van een constructie die de ‘Wilsonoperator’ WK heet.
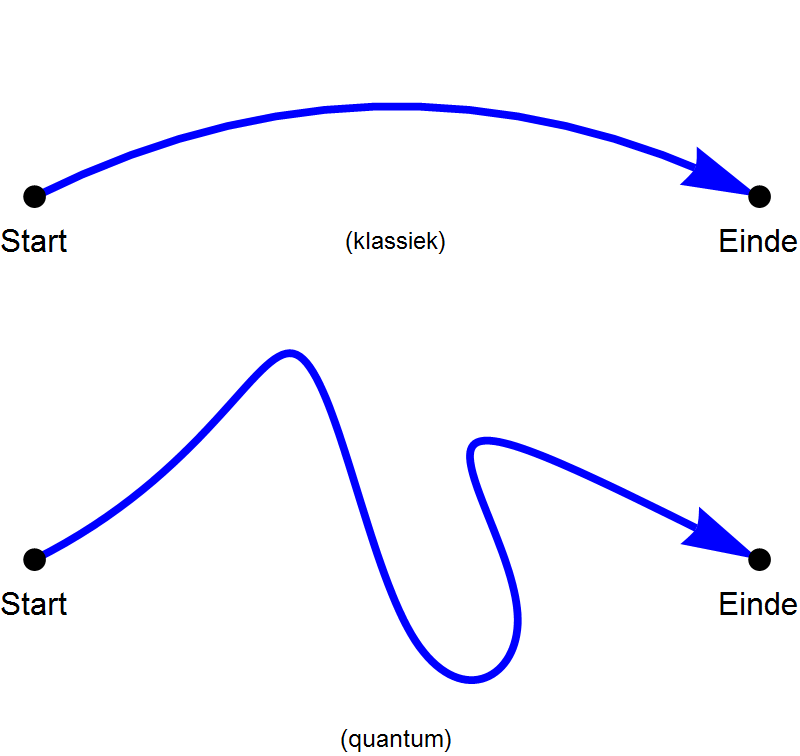
Afbeelding 4. Paden in de klassieke en de quantumfysica.Boven: pad van een klassiek deeltje. Onder: één mogelijk pad van een quantumdeeltje.
Wat dus ook kan gebeuren, is dat een deeltje het pad volgt uit afbeelding 5 hieronder.. Dit pad kan je wiskundig zien als een knoop, als je het start- en eindpunt aan elkaar zou plakken. Witten heeft laten zien, dat de waarde van WK, gemiddeld over alle “quantummogelijkheden” en aangegeven met
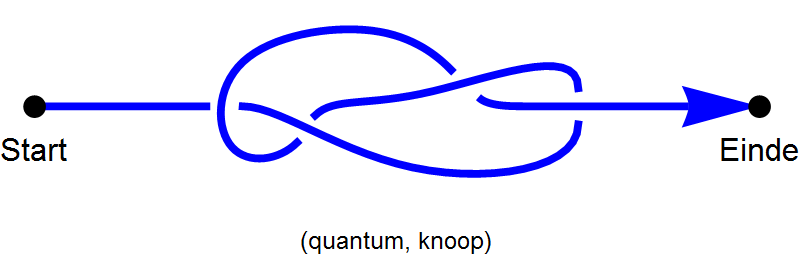
Afbeelding 5. Een quantumknoop.Mogelijk pad van een quantumdeeltje met een knoop.
Omdat het Jonespolynoom, net als knopen in het algemeen, in drie dimensies is gedefiniëerd, correspondeert het ook met een quantumtheorie in drie dimensies. Nu leven wij, en de quantumdeeltjes in onze wereld dus ook, in een vierdimensionale wereld: drie ruimtedimensies en één tijdsdimensie. De ontdekking van Witten heeft een heleboel nieuwe ontdekkingen in gang gezet, waaronder ook theorieën die paden in een vierdimensionale wereld koppelen aan invarianten van “vormen” in vier dimensies, die een stuk minder makkelijk zijn om voor te stellen. Het onderzoeksgebied dat begon in 1989 is dus nog altijd volop in ontwikkeling!