De klassieke wereld is namelijk ook niet altijd zo eenvoudig. Zo kom je daar chaotische systemen tegen, waarin het gedrag van een systeem zó gevoelig is voor kleine verstoringen, dat het vrijwel onmogelijk is om er iets over te voorspellen. Het is alsof een vlinderslag in Jakarta genoeg zou zijn om in orkaan bij Florida te veroorzaken. Een interessante vraag is natuurlijk: wat gebeurt er wanneer we een deeltje in een klassiek chaotisch systeem op quantumniveau zouden beschrijven? Bestaat er zoiets als quantumchaos?
Chaotisch biljarten
Om die vraag te kunnen beantwoorden moeten we eerst weten hoe een klassiek chaotisch systeem eruitziet. Hoewel chaostheorie veel wordt gebruikt om het gedrag van complexe systemen zoals de aandelenmarkt en dierenpopulaties in de natuur te beschrijven, kunnen ook eenvoudige systemen chaotisch zijn. Neem bijvoorbeeld een biljartbal, die je laat rondkaatsen op een stadion-vormige tafel met een verhoogde rand. Als je de bal precies goed zou mikken, zou je die in een herhalend (periodiek) patroon kunnen laten bewegen; voorbeelden van zulke patronen zie je in afbeelding 1. Als je dit in het echt zou proberen, zul je echter snel merken dat dit heel erg moeilijk te doen is! Als de bal net een beetje scheef begint, raakt hij steeds punten van de tafelrand net náást de eerder geraakte punten. Als de tafel oneindig glad zou zijn, en de wrijving dus geen roet in het eten zou gooien, zou de bal eindeloos heen en weer kaatsen en uiteindelijk alle punten van de rand van de tafel raken. De periodieke bewegingen zijn extreem instabiel: de bal zal vrijwel altijd ‘chaotisch’ rondkaatsen.
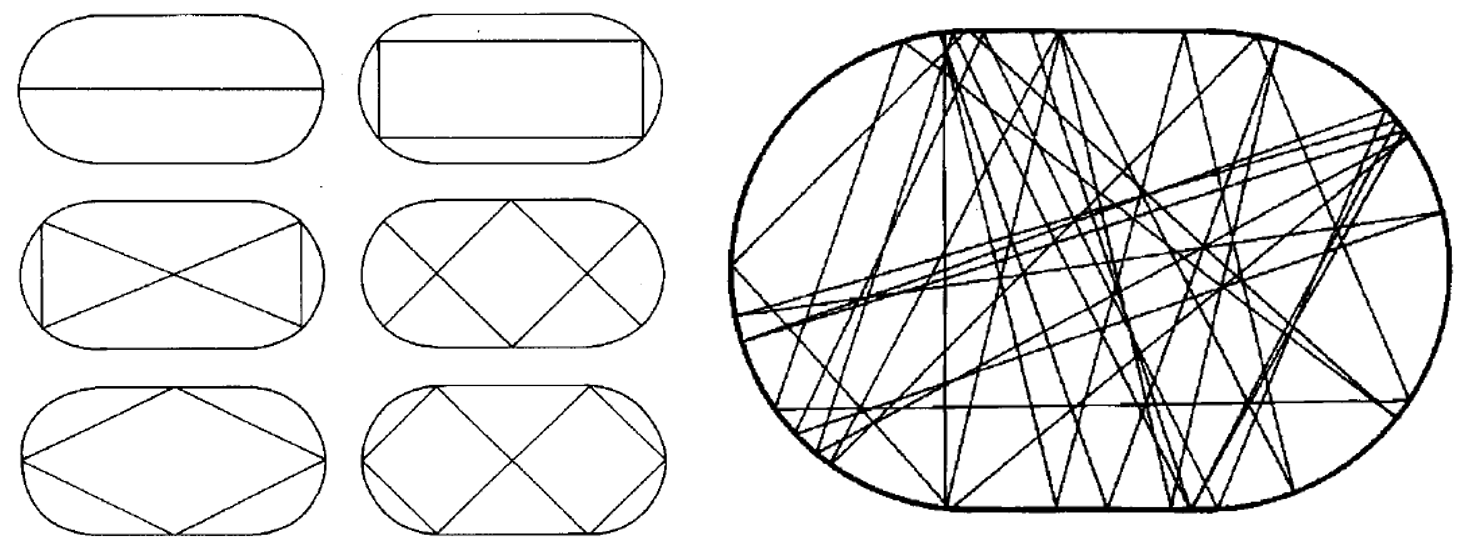
Afbeelding 1. Stableie en chaotische banen. Links: mogelijke periodieke banen van de biljartbal. Deze banen zijn instabiel. Rechts: een bewegingspatroon vanuit een minder bijzondere beginsituatie. Afbeeldingen uit referentie [1].
Van klassiek naar quantummechanisch
In de natuurkunde houden we van eenvoudige voorbeelden, dus het voorbeeld hierboven is een perfect beginpunt. Wat zou er gebeuren als we onze klassieke biljartbal zouden vervangen door een quantummechanisch deeltje? Ten eerste kunnen we zo’n deeltje niet op dezelfde manier beschrijven. In de klassieke wereld zijn gebeurtenissen inherent deterministisch: dat wil zeggen dat je in principe precies kunt voorspellen wat er gebeurt als je onze (nog stilliggende) biljartbal een zetje geeft. We weten zeker dat de bal dan in de richting van het zetje zal voortbewegen, en bijvoorbeeld niet zomaar achteruit. In de quantumwereld daarentegen is alles juist probabilistisch – dingen worden beschreven met kansen. Quantumdeeltjes hebben geen exacte positie en snelheid, maar worden beschreven met een golffunctie. (Zie hierover ook ons dossier over quantumfysica.) In dit voorbeeld hangt deze functie alleen af van de tijd en van de positie van de bal op de tafel, en het kwadraat van de golffunctie op een bepaalde plek bepaalt de kans dat je, als je op dat moment naar de tafel zou kijken, de bal op die plek zal vinden.
De toegestane golffuncties van een deeltje dat “in een doos” is opgesloten (in het Engels: particle in a box) is een van de meest bestudeerde problemen van de quantumfysica. Volgens de beroemde Schrödingervergelijking zijn er namelijk maar bepaalde golffuncties die in de doos zouden ‘passen’. Preciezer geformuleerd: de mogelijke energieën van de toestanden waarin het deeltje kan zijn, zijn gequantiseerd – niet elke energie is dus mogelijk. In de jaren ’80 berekende de Amerikaanse natuurkundige Eric Heller welke golffuncties er in een (tweedimensionale) stadion-vormige doos zouden passen – de quantumversie van onze chaotische biljartbal. Hier ontdekte hij iets merkwaardigs: in de vorm van de toegestane golffuncties (en dus ook in de kansverdeling van waar je een deeltje zou vinden als je een meting zou doen) kon hij dezelfde instabiele, periodieke banen van de klassieke biljartbal zien!
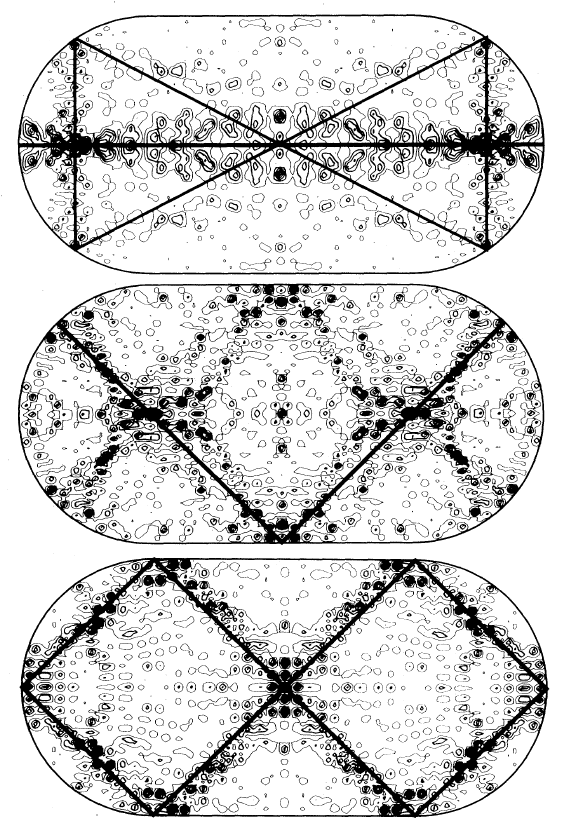
Afbeelding 2. Een quantumbiljart. Mogelijke golffuncties in een stadion-vormige doos; waar de afbeelding donkerder is, is de kans groter dat je het deeltje er zou kunnen aantreffen. De herkenbare klassieke periodieke banen zijn ook getekend. Afbeelding uit referentie [2].
Heller noemde dit effect quantum scars, dat wil zeggen: quantumlittekens. Het lijkt namelijk alsof de klassieke periodieke banen van de biljartbal hun afdruk hebben achtergelaten in de quantummechanische golffuncties. Waar het in een klassiek chaotisch systeem vrijwel onmogelijk is om een deeltje in een herhalende baan te krijgen, en het deeltje juist alle mogelijke posities zal bezoeken, werkt het in de quantumwereld juist andersom! In een quantumsysteem waarvan de klassieke versie chaotisch is, zoeken de golffuncties – en dus de quantumdeeltjes – juist de periodieke banen op.
Coole (koele) qubits
Quantum scars lijken misschien een abstract fenomeen, maar zo’n 35 jaar na de ontdekking van Heller is het idee opnieuw tot leven gekomen, in de context van quantum computing. Als tussenstap op weg naar een volledige, werkende quantumcomputer, maakte een onderzoeksgroep van het Massachusetts Institute of Technology (MIT) een zogeheten ‘quantumsimulator’ [3]. Die simulator bestaat uit een rij van 51 atomen die op lage temperatuur met behulp van lasers en magneetvelden in een net rijtje worden geplaatst. Ieder atoom zit óf in de grondtoestand – de toestand met de laagst mogelijke energie – óf wordt geprepareerd in de aangeslagen ‘Rydbergtoestand’, waarin het buitenste elektron van het atoom in zo’n grote baan om de kern draait dat het atoom bijna geïoniseerd is. Deze twee toestanden zijn de ‘0’ en de ‘1’-toestanden van de 51 quantumbits (qubits), en in die bits kan het systeem informatie opslaan.

Afbeelding 3. 51 qubits. Drie afbeeldingen van de 51 qubits van in de quantumsimulator van MIT. Atomen in de grondtoestand zijn groen, terwijl de atomen die met roze cirkels zijn weergegeven zich in de aangeslagen Rydbergtoestand bevinden. De zwarte ovalen geven aan waar er twee atomen in dezelfde toestand naast elkaar staan. Afbeelding uit referentie [3].
Met hun opstelling kon het team van MIT niet alleen de exacte begintoestand van hun qubits kiezen, maar ook precies meten hoe lang het duurde totdat hun qubits zodanig verstoord waren dat de opgeslagen informatie verloren raakte. Hierbij deden ze een verrassende ontdekking: sommige toestanden, zoals wanneer ieder tweede atoom geprepareerd werd in de Rydbergtoestand (onderste rij in afbeelding 3), bleven wel tien keer langer stabiel dan andere toestanden! Dit is een interessant resultaat voor ontwikkelaars van quantumcomputers, want de stabiliteit van qubits is een van de grootste struikelblokken voor het bouwen van een echte quantumcomputer.
De beste verklaring die tot nu toe voor deze onverwachte stabiliteit is gevonden, is dat dit een voorbeeld is van ‘many-body quantum scarring’ – hetzelfde effect als in het quantumbiljart dat we eerder bekeken, dus. De gezamenlijke toestand van qubits heeft, net als de quantumbiljartbal, een intrinsieke voorkeur voor de bijzondere, periodieke aangeslagen toestand, waardoor toestanden zoals deze langer stabiel blijven. De precieze details van hoe dit alles werkt zijn echter nog lang niet helemaal uitgewerkt. Er is dus nog veel werk voor de boeg, maar zou goed kunnen dat dit effect de truc blijkt te zijn die we uiteindelijk nodig hebben om stabiel werkende, mobiele quantumcomputers mogelijk te maken.
Referenties
[1] E. Arcos, et al. Vibrating soap films: An analog for quantum chaos on billiards. American Journal of Physics 66(7); 1997.
[2] E.J. Heller. Bound-state eigenfunctions of classically chaotic Hamiltonian systems: Scars of periodic orbits. Physical Review Letters 53(16); 1984.
[3] H. Bernien et al.Probing many-body dynamics on a 51-atom quantum simulator. Nature 551; 2017.