Grafeen is een bijzondere soort metaal. Naast dat ze goed zijn in het geleiden van stroom en warmte, gedragen de elektronen in grafeen zich in zekere zin als relativistische deeltjes, toont de stof het quantum-Halleffect, is het meer dan honderd keer sterker dan het sterkste staal, en tegelijkertijd extreem rekbaar. Een denkbeeldige hangmat gemaakt van grafeen zou het gewicht van een kat kunnen dragen, ondanks dat het materiaal door de ene atoom dikte bijna onzichtbaar zou zijn en minder zou wegen dan één van de snorharen van de kat! (Zie ook ons eerdere artikel over grafeen.)
Afbeelding 1. Een kat in een grafeen-hangmat. Eigen werk; kattentekening van XuLily.
Hoewel een enkele laag van grafeen dus al zeer interessant is, ontdekte de onderzoeksgroep van Jerillo-Herrero dat twéé lagen grafeen samen nog heel andere eigenschappen toonden, en dat deze eigenschappen sterk afhingen van hoe de twee lagen precies op elkaar gelegd waren. Meer precies gezegd: als de ene laag een heel klein beetje gedraaid op te andere werd gelegd, veranderde het geheel bij bij lage temperaturen en een ‘magische’ draaihoek van rond 1,1° van een geleidend metaal naar een isolator, of zelfs een supergeleider, waarin stroom geen enkele weerstand voelt! Dat een kleine draaiing zulke grote veranderingen in geleidingseigenschappen tot gevolg kon hebben had niemand verwacht.
In zekere zin is het intuïtief goed te begrijpen dat draaiing de elektronische eigenschappen van twee op-elkaar-gestapelde materialen zou kunnen veranderen. Materialen zijn immers opgebouwd uit verzamelingen atomen, en rotatie van een van de twee lagen zou kunnen veranderen hoe dicht individuele atomen in de twee lagen bij elkaar komen, en dus hoe makkelijk elektronen van het ene atoom naar het andere atoom zouden kunnen bewegen. Het was ook al theoretisch voorspeld dat draaiing iets zou kunnen veranderen – maar beslist niet zoveel als in de experimenten van Jerillo-Herrero gezien werd. Hoe werkt dit allemaal, en waarom werden vaste-stoffysici hier zo enthousiast over?
Een stapje terug: hoe werkt geleiding?
Waarom sommige materialen stroom geleiden, en andere niet, is een van de fundamentele vraagstukken waarmee vaste-stoffysici zich bezighouden. Hoewel de vraag eenvoudig genoeg klinkt, heeft de natuur (gelukkig) de neiging om toch een tikkeltje diverser en ingewikkelder te zijn dan je misschien zou verwachten. Zo hebben natuurkundigen intussen al ontdekt dat er, naast normale geleiders (oftewel: metalen) en isolatoren, ook exotischere materialen bestaan als halfgeleiders, semimetalen, topologische isolatoren, en supergeleiders.
Hoe (normale) geleiding werkt kun je grotendeels begrijpen in termen van zogeheten energiebanden. (Zie voor meer gedetailleerde informatie ons dossier hierover.) Geleiding beschrijven in termen van energiebanden is een aanpak die vooral goed werkt in goed geordende vaste stoffen, waarin atomen gerangschikt zijn in een herhalend patroon dat we een kristalrooster noemen.
Afhankelijk van de vorm van dit rooster en de soorten atomen erin, kunnen elektronen – die zich in het materiaal eerder gedragen als quantummechanische golven dan als deeltjes – alleen bepaalde combinaties van energieën en golflengtes hebben. Welke combinaties mogelijk zijn, kun je weergeven als een verzameling van energiebanden En(k), waar E de elektronenergie is, k de impuls van het elektron, en n aangeeft over welke energieband je het hebt. De impuls is invers gerelateerd aan de golflengte van de elektrongolf: een grotere impuls komt overeen met een kleinere golflengte. Door de periodiciteit van het rooster zullen de energiebanden En(k) ook periodiek zijn, en zien ze er meestal sinusvormig uit. Zo is de periodiciteit van het kristalrooster dus terug te zien in de energiebanden van de elektronen.
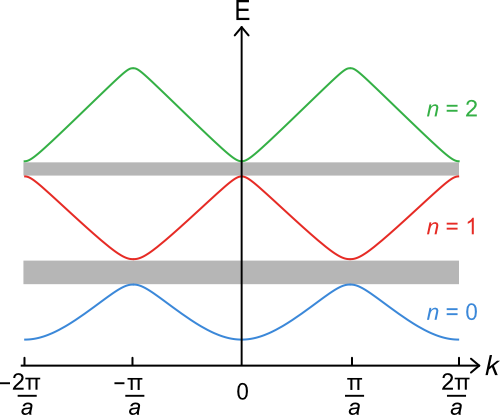
Afbeelding 2. Energiebanden van een ééndimensionaal kristal De eerste drie energiebanden van een ééndimensionale keten van atomen die allemaal op afstand a van elkaar staan. Ook de bandenstructuur is periodiek, met een periodiciteit van k=2π/a. De grijze vlakken geven bandkloven aan: energieën die voor elektronen in dit systeem verboden zijn. Afbeelding: Robert Nolty, aangepast.
Of een materiaal stroom kan geleiden of niet, is te zien aan tot welke energie de elektronen in de energiebanden zitten. Dankzij het uitsluitingsprincipe van Pauli kunnen twee elektronen zich nooit in precies dezelfde toestand bevinden. Dat wil zeggen: geen twee elektronen (met dezelfde spin) kunnen precies dezelfde energie en impuls hebben. Zo ‘vullen’ elektronen de energiebanden vanaf de laagste energie, en zijn het de elektronen met de hoogste energie die stroom kunnen geleiden. Als de hoogste-energie elektronen helemaal bovenaan een energieband zitten, en net ónder een reeks energieën waar geen energieband zit (een bandkloof), dan kan het materiaal géén stroom geleiden en is het een isolator. Zitten de geleidingselektronen ergens midden in een energieband, dan is het materiaal een metaal.
De vorm van de energieband waar de geleidingselektronen in zitten bepaalt hoe makkelijk ze door het kristal kunnen bewegen. Zo geeft de helling van de band aan hoe snel elektronen door het materiaal bewegen, terwijl de kromming van de band aangeeft wat de effectieve massa van de geleidingselektronen is. In tegenstelling tot het (simpelst-mogelijke) voorbeeld van afbeelding 2, kunnen echte materialen complexe bandenstructuren hebben, maar de analyse ervan blijft hetzelfde.
Toveren met superroosters
Nu we de basisprincipes van energiebanden kennen, komen we bij de vraag hoe draaiing de geleidingseigenschappen van een dubbellaag van grafeen kan veranderen. Wanneer je twee tweedimensionale kristalroosters op elkaar stapelt die niet precies op elkaar passen, bijvoorbeeld omdat een van de twee roosters gedraaid is ten opzichte van de ander, zul je zien dat er een veel grootschaliger patroon ontstaat. Dit heet een moiré-superrooster.
Video 1. Het draai-afhankelijke moiré-superrooster van een dubbellaag grafeen. Auteur: PMende.
Zoals te zien in de korte video hierboven verandert de structuur van het superrooster enorm als we de draaihoek veranderen. Zoals hierboven besproken, bepaalt de periodiciteit van het kristalrooster ook de periodiciteit van de energiebanden van de elektronen. De superroosters kunnen, afhankelijk van de draaihoek, een periode hebben van tientallen of zelfs honderden atomen. Veel groter dan de roosterafstand van de aparte grafeen-kristalroosters, dus, en dat betekent dat de energiebanden juist een veel kleinere periodiciteit moeten hebben. Interacties tussen de twee grafeenlagen, die ook veranderen afhankelijk van de draaihoek, zullen bovendien de energiebanden vervormen.
Door de structuur van het superrooster onstaan er bij sommige ‘magische’ draaihoeken energiebanden die vrijwel helemaal plat zijn. Dat wil zeggen: deze energiebanden hebben voor een hele reeks van impulsen bijna geen energie-afhankelijkheid. Elektronen in zo’n platte band hebben een extreem lage snelheid, en gedragen zich alsof ze heel zwaar zijn: ze komen als het ware bijna stil te staan!
Omdat de elektronen in de platte energiebanden zowat stilstaan, kunnen ze elkaars aanwezigheid veel sterker voelen. Door deze sterke elektron-elektroninteracties kunnen de elektronen vast komen te zitten en isolerend gedrag tonen – ze vormen dan een zogeheten Mott-isolator. Nog interessanter is dat deze versterkte interactie tussen elektronen er ook voor kan zorgen dat ze elektronparen vormen, die kunnen supergeleiden. Het exacte mechanisme van de supergeleiding in gedraaide dubbellagen van grafeen is nog niet goed begrepen, maar het lijkt erop dat de werking vergelijkbaar is met wat er in hogetemperatuursupergeleiders gebeurt. Door de supergeleiding in gedraaide dubbellagen grafeen verder te bestuderen, leren we wellicht ook iets over de werking van andere onconventionele supergeleiders.
Van ‘twisted’ grafeen naar twistronics
Hoewel het interessant is dat een dubbellaag grafeen supergeleidend kan worden, was dit nog maar het begin van wat inmiddels een heel nieuw onderzoeksgebied is geworden. Naast supergeleiding tonen gedraaide dubbellagen grafeen ook nog eens interessante magnetische en zelfs topologische fasen, waardoor de studie van dit materiaal een zeer interessant speelveld blijkt om een breed scala van interessante fysica te bestuderen. Ondertussen zijn onderzoekers er al in geslaagd om apparaatjes te maken waarin de draaihoek tussen twee lagen makkelijk aangepast kan worden: het begin van instelbaar twistronisch apparatuur. En niet alleen grafeen is interessant om naar te kijken: ook tweedimensionale halfgeleiders zoals hexaboronnitride (hBN) en WSe2 vertonen interessant draai-afhankelijk gedrag. Verder worden systemen met meer dan twee lagen onderzocht, zoals een opeenstapeling van vier lagen grafeen met een draaiing tussen de middelste twee lagen, of een gecombineerde structuur van hBN-grafeen-hBN. Meer lagen betekent immers dat er nog meer en nog grotere moiré-superroosters mogelijk zijn, en dat je dus ook nieuwe exotische fases kunt creëren.
Het is moeilijk om alle nieuwe ontdekkingen bij te houden, omdat er in de laatste paar jaar honderden wetenschappelijke artikelen zijn gepubliceerd over twistronics, “twisted bilayer graphene” (gedraaide dubbellaags-grafeen), en andere variaties van gestapelde tweedimensionale materialen met een draaiing ertussen. Naar verwachting zullen er daar ook nog wel honderden bij komen. Voorlopig zal de studie van twistronics blijven bij fundamenteel onderzoek naar exotische fasen, maar wie weet hebben we over enkele jaren allemaal een twistronica-gadget in onze zak!