Afbeelding 1. Grafeen.Grafeen is een materiaal dat het quantum-Hall-effect vertoont. Deze afbeelding, op atomaire schaal, is gemaakt met een Scanning Probe-Microscoop. Afbeelding: US Army Materiel Command.
Voordat we echt gaan kijken naar topologische isolatoren, wil ik eerst toelichten wat isolatoren zijn. Isolatoren zijn materialen die niet geleiden bij kamertemperatuur. Dit betekent dat de elektronen in het rooster die voor geleiding zorgen, niet of nauwelijks kunnen bewegen. De reden hiervoor is dat alle toestanden waarin een elektron zich bij kamertemperatuur kan bevinden bezet zijn. en er dus geen mogelijkheid is om van de ene naar de andere toestand te gaan. Het veranderen van toestand zorgt voor geleiding en is in dit geval dus onmogelijk. Verhoog je nu de temperatuur zodanig dat er nieuwe toestanden voor het elektron beschikbaar komen, dan kan er wel weer geleiding optreden en wordt de isolator een metaal.
Topologische isolatoren zijn een beetje gekke isolatoren. Ze zijn namelijk niet helemaal een isolator; deze materialen geleiden wel aan de buitenkant, maar niet aan de binnenkant. Dit bekent dat, als je een spanningsverschil aanlegt over het materiaal, de resulterende stroom liever over het oppervlak dan door de binnenkant loopt. Het feit dat deze materialen deze eigenschap hebben, heeft alles te maken met het bijvoegelijk naamwoord topologische in ’topologische isolatoren’.
Laat ik dit toelichten. Ter herinnering: topologie beschrijft de eigenschappen van voorwerpen die niet veranderen als we het voorwerp geleidelijk vervormen. Ten eerste is het oppervlak een topologische eigenschap van een materiaal, want je komt er niet zomaar vanaf door het materiaal op een continue wijze te vervormen. Als je een gat zou boren kun je natuurlijk wel meer oppervlak creëren en kan er ook weer een stroom gaan lopen in het nieuw gemaakte oppervlak. Ten tweede is de topologie ook terug te vinden in de toestanden van de elektronen in het materiaal. Normaliter beschrijven we deze toestanden door naar hun impuls en energiebanden te kijken (zie ons dossier over quantumtoepassingen) en vanuit dat oogpunt is de topologie goed zichtbaar. De energiebanden kunnen namelijk op een dusdanige manier in elkaar vervlochten zijn dat ze niet op een continue wijze ontvlochten kunnen worden. Het feit dat deze banden zo verstrengeld zijn is precies ook de reden waarom er over het oppervlak wel een stroom kan lopen, maar door de binnenkant niet. Daarnaast zorgt het ook voor een zekere robuustheid van die stroom, aangezien je niet op een continue wijze van de vervlochten energiebanden af kunt komen. Nu kun je ook begrijpen waarom deze materialen zo geschikt zijn voor quantumcomputers, want de qubits die je daarvoor nodig hebt moeten robuuste eigenschappen hebben om goed te kunnen functioneren. Topologische isolatoren en topologische materialen in het algemeen bieden precies deze robuuste eigenschappen.
Het simpelste en oudste voorbeeld van een topologische isolator is het quantum-Hall-systeem. Stel je een kristal voor in twee dimensies met daarin elektronen en stel dat er een homogeen magneetveld loodrecht op dat rooster staat. De elektronen voelen dat magneetveld en we kunnen ze quantummechanisch beschrijven met een golffunctie die voldoet aan de Schrödingervergelijking. Zoals vaak het geval is in de quantummechanica, kunnen de elektronen zich maar in bepaalde energieniveaus bevinden. Denk bijvoorbeeld aan de energieniveaus van het waterstofatoom. In het quantum-Hall-systeem worden die energieniveaus Landauniveaus genoemd, naar de Sovjet-Russische natuurkundige Lev Landau. Elektronen kunnen zich in deze energieniveaus bevinden, maar om van het ene niveau naar het andere te gaan is veel energie nodig – zodanig veel dat het materiaal een isolator is. Kijk je echter naar de eendimensionale rand van het tweedimensionale kristal, dan zul je zien dat er daar wel geleiding mogelijk is. Deze geleiding blijkt heel speciaal te zijn en blijkt alles te maken hebben met een verscholen topologie in het quantum-Hall-systeem.
Om deze topologie te vinden, moeten we de geleiding op de rand beter bestuderen. Hiervoor hebben we een grootheid nodig die aangeeft wanneer een materiaal goed en wanneer een materiaal slecht geleidt. Deze grootheid heet de conductiviteit: hoe groter de conductiviteit, hoe beter de geleiding. Voor het quantum-Hall-systeem wordt deze conductiviteit de Hall-conductiviteit genoemd. Uit experimenteel onderzoek door Klaus von Klitzing in de jaren ’80 bleek dat de Hall-conducitviteit alleen heel speciale waarden aanneemt, en in stappen verandert wanneer het magneetveld verhoogd wordt, zoals je kunt zien in afbeelding 2.
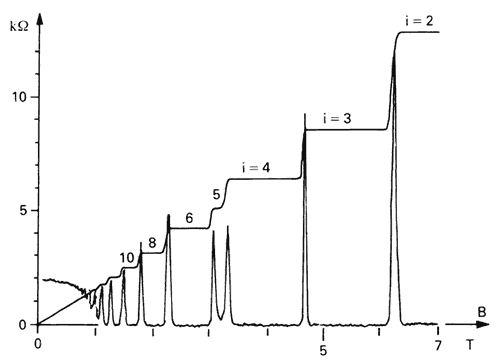
Afbeelding 2. Het quantum-Hall-effect.Je ziet hier de Hall-resistiviteit (dat is één gedeeld door de Hall-conductiviteit) in kilo-ohm geplot tegen het magneetveld in Tesla. De gepiekte grafiek is voor dit artikel niet van belang. Je ziet dat de andere grafiek een heel duidelijk traptreden-patroon vertoont en elke keer dat als i groter wordt (n in de onderstaande formule), de resistiviteit afneemt en dus de conductiviteit toeneemt. Merk op dat de hoogte van de stapjes verandert omdat je deelt door i (of n in de formule hieronder). Bron: Nobelprize.org.
De stappen waarmee de geleiding verandert, hebben altijd exact dezelfde waarde, namelijk e2/h, waarbij e de elementaire lading is (dat wil zeggen: de grootte van de lading van het elektron) en h de constante van Planck. We kunnen de Hall conductiviteit, die we noteren als σxy, dus schrijven als
σxy = n · e2/h
waar n een geheel getal is. Het feit dat n een geheel getal is, heeft alles met de verstrengeling van energiebanden te maken. Als n gelijk is aan nul, zijn de banden niet verstrengeld en hebben we te maken met een gewone isolator. Is n ongelijk aan nul, dan is er wel verstrengeling aanwezig en is de isolator topologisch. Op de rand heeft n ook een betekenis; het is namelijk het aantal vrijheidsgraden (ofwel het aantal quantumvelden) dat meedoet aan de geleiding. Dit getal kan ook negatief zijn: dat betekent alleen dat de stroom de andere kant op gaat.
Voor de meting van het quantum-Hall-effect ontving Klaus von Klitzing in 1985 de Nobelprijs. Dit was niet alleen experimenteel een waanzinnige meting, maar was ook de grondslag van een nieuw vakgebied: dat van de topologische materialen. Theoretisch is deze meting ook van grote invloed geweest. Zoals je hierboven hebt kunnen lezen is er een diepe connectie tussen de Hall-conductiviteit, de verstrengeling van energiebanden en het aantal quantumvelden op de rand van het materiaal. Door middel van mooie wiskundige resultaten kunnen we deze connectie heel precies maken en begrijpen we tegenwoordig waarom sommige materialen dit effect vertonen.
We hebben nu een voorbeeld van een topologische isolator gezien, maar topologische materialen in het algemeen bevatten veel meer interessante natuurkunde dan alleen het quantum-Hall-effect. Zo zijn er ook topologische materialen die invariant zijn onder tijdsomkering en waar er ook weer geleiding is langs de rand en niet door de binnenkant. Een bespreking van dit type bewaren we echter voor een volgend artikel. We zullen dan meer ingaan op tijdsomkering precies doet met energiebanden en waarom de Nederlandse natuurkundige Hans Kramers hier een sleutelrol in speelt.
Meer weten?
Het quantum-Hall-effect is een enorm interessant effect, maar technisch lastig te begrijpen – we hebben hierboven dan ook alleen een eerste tip van de sluier opgelicht, en de nodige wiskundge details achterwege gelaten. Wie meer wil weten en al wat eenvoudige quantummechanica beheerst kan bijvoorbeeld eens kijken op deze pagina van David Tong voor verdere technische informatie.