
Afbeelding 1. The Matrix?Wat is een matrix nu eigenlijk echt, en wat heb je eraan? Afbeelding: Max Pixel.
In de film doelt het begrip matrix op de `schijnwereld’ waarin de personages leven. Een natuurkundige heeft echter een volledig ander (maar niet minder spannend) idee bij het begrip matrix. Dit artikel is het eerste in een reeks artikelen die gewijd is aan de interessante en onverwachte toepassingen van matrices binnen de natuurkunde.
Wat is een matrix?
Simpel gezegd is een matrix niets meer dan een tabel met getallen. De grootte van de matrix wordt bepaald door het aantal rijen en kolommen in de tabel. We zijn hier voornamelijk geïnteresseerd in vierkante matrices, met evenveel rijen als kolommen. Een voorbeeld van een matrix met twee rijen en kolommen is
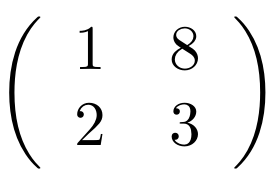
Zo’n matrix lijkt op het eerste gezicht niet erg spannend: eerder een handig begrip voor boekhouders dan voor natuurkundigen. Het blijkt echter dat veel fenomenen en processen binnen de natuurkunde, maar ook daarbuiten, goed kunnen worden beschreven in termen van matrices. De theorie van het rekenen met matrices – ook wel lineaire algebra genoemd – is een van meest gebruikte wiskundige gereedschappen binnen de natuurkunde. In het kort is het idee hierachter dat een matrix niet zomaar een statisch object is, maar dat deze objecten ook met elkaar – en met vectoren – kunnen worden vermenigvuldigd. Dat vectoren, rijtjes van getallen, ook in deze theorie voorkomen is niet zo vreemd: een vector is immers een matrix met één kolom. Doordat we met matrices alle bewerkingen kunnen uitvoeren die we ook met getallen kunnen doen, kunnen we matrices zien als dynamische objecten die natuurkundige processen kunnen beschrijven.
Zoals je misschien zelf al eens hebt ervaren is het vermenigvuldigen van twee matrices een hele klus: het is niet simpelweg element per element vermenigvuldigen, maar er is een ingewikkeldere procedure om het matrixproduct te vinden. Voor ons verhaal is het vooral belangrijk om te noemen dat het product van twee diagonaalmatrices wel makkelijk is uit te rekenen. Een diagonaalmatrix is een vierkante matrix met overal nullen behalve op de diagonaal. Bijvoorbeeld:
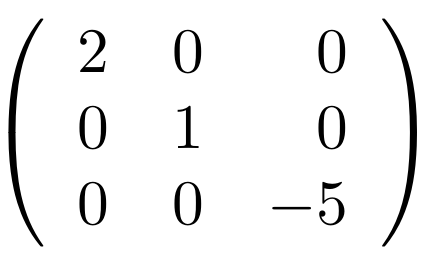
Voor diagonaalmatrices is het product wel element voor element uit te rekenen: je vermenigvuldigt het eerste diagonaalelement van de eerste matrix met het eerste diagonaalelement van de tweede, dan beide tweede diagonaalelementen, enzovoort, en bouwt zo de productmatrix op. Merk trouwens op dat dit alleen werkt als de matrices even groot zijn – je kunt dus niet zomaar alle matrices met elkaar vermenigvuldigen!
Om matrices makkelijk te kunnen vermenigvuldigen is het dus nuttig om te weten hoe je een matrix in diagonaalvorm kunt brengen. We zullen hier niet uitleggen hoe je dit in de praktijk moet doen – dit proces heet diagonaliseren – maar het is voor nu voldoende om op te merken dat als de matrix aan bepaalde eisen voldoet (bijvoorbeeld als hij bepaalde symmetrieën heeft) je dit altijd kunt doen. De elementen op de diagonaal heten dan de eigenwaarden van de matrix. Deze eigenwaarden zijn in veel gevallen de belangrijke getallen om uit te rekenen als je een matrix bestudeert.
Matrices in de quantummechanica
Een plek waar matrices een belangrijke rol spelen is in de quantummechanica – de theorie die deeltjes op de allerkleinste schaal probeert te beschrijven. Een van de grondbeginselen van de quantummechanica zegt dat de toestand van een deeltje, bijvoorbeeld een elektron, wordt beschreven door een vector en dat de tijdsevolutie van het deeltje wordt beschreven door een matrix, de zogenaamde Hamiltoniaan. Door de vector met de Hamiltoniaan te vermenigvuldigen krijgen we een nieuwe vector die gebruikt kan worden om de toestand ven het deeltje op een iets later tijdstip te beschrijven. Deze regel staat in de quantummechanica ook wel bekend als de Schrödingervergelijking.
De kunst is nu om de Hamiltoniaan van het systeem te diagonaliseren. De eigenwaarden van deze matrix kun je namelijk natuurkundig interpreteren als de energieniveaus van het deeltje dat je probeert te beschrijven. Een van de grootste successen – en een belangrijke experimentele toets – van de quantummechanica was het succesvol beschrijven van de energieniveaus van het waterstofatoom. De Hamiltoniaan behorende bij het waterstofatoom kan namelijk worden gediagonaliseerd en – hoewel dit zeker geen makkelijke berekening is – blijken de eigenwaarden zoals verwacht precies overeen te komen met het energiespectrum dat door experimenten was bepaald. Een mooie test voor het matrixformalisme in de quantummechanica!
Zware atoomkernen en Wigners vermoeden
In de jaren 50 deed de Hongaars-Amerikaanse natuurkundige Eugene Wigner onderzoek naar het energiespectrum van zware atoomkernen, zoals uranium en thorium. Hoewel deze atomen theoretisch veel moeilijker te beschrijven zijn dan het simpele waterstofatoom, konden ze experimenteel goed worden bestudeerd met behulp van neutronenverstrooiing: het laten botsen van neutronen met de kernen en bestuderen wat er vervolgens met de neutronen gebeurt.
Het probleem dat Wigner tegenkwam was tweeledig: het aantal energieniveaus van zware atoomkernen dat door experimenten was gevonden was enorm groot, én er was niet veel structuur in te herkennen. In de experimentele data komen de energieniveaus overeen met piekjes in de zogeheten diffusiecoëfficiënt van de neutronen uitgezet tegen de neutronenergie. Een voorbeeld van een dergelijke grafiek die Wigner theoretisch probeerde te verklaren is hieronder weergeven.
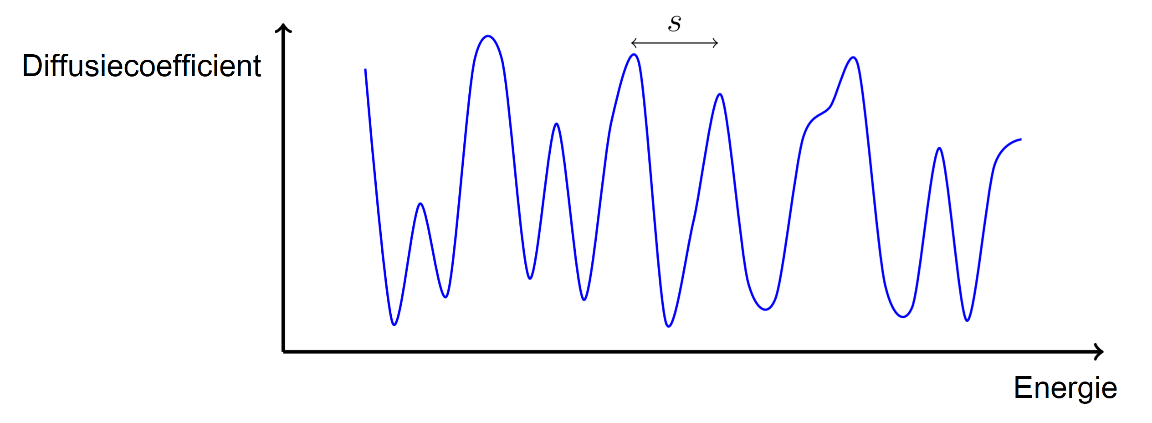
Afbeelding 2. De diffusiecoëfficiënt.Met behulp van matrices kunnen we de afstand tussen de pieken begrijpen!
Op het eerste gezicht lijkt er niet veel regelmaat in deze grafiek te zitten, maar dat bleek schijn. Door het grote aantal energiepiekjes in het spectrum is het handig om naar statistische grootheden te kijken. Een belangrijke variabele waarin Wigner geïnteresseerd was, is de afstand tussen twee opeenvolgende piekjes. De verdeling van deze afstanden blijkt sterk te lijken op die van een zuiver kansproces. De grote vraag is dan natuurlijk welk kansproces deze verdeling veroorzaakt. Het antwoord dat Wigner vond was de volgende formule:
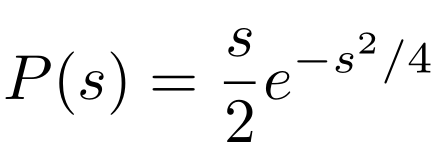
Met P(s) bedoelen we de kans[1] dat de afstand tussen twee piekjes gelijk is aan s. Deze formule staat bekend als `Wigners surmise’. Het feit dat deze formule nog steeds bekend staat als een `surmise’ (=vermoeden) komt voort uit de volgende anekdote. Op een conferentie over neutronenfysica in Oak Ridge National Laboratory in 1956 werd de vraag gesteld of het mogelijk was om de kansverdeling voor afstanden tussen energieniveaus te beschrijven voor een zwaar atoom. Wigner, die op dat moment in het publiek zat, liep naar voren en `vermoedde’ het antwoord dat hierboven staat door de bijbehorende grafiek op het krijtbord te tekenen. Het gedrag van Wigners verdeling is anders dan je zou verwachten als de energieniveaus volkomen onafhankelijk van elkaar zijn. In dat geval zou de kansverdeling eerder de vorm hebben van een zogenaamde Poissonverdeling. In een grafiek is het verschil goed te zien:
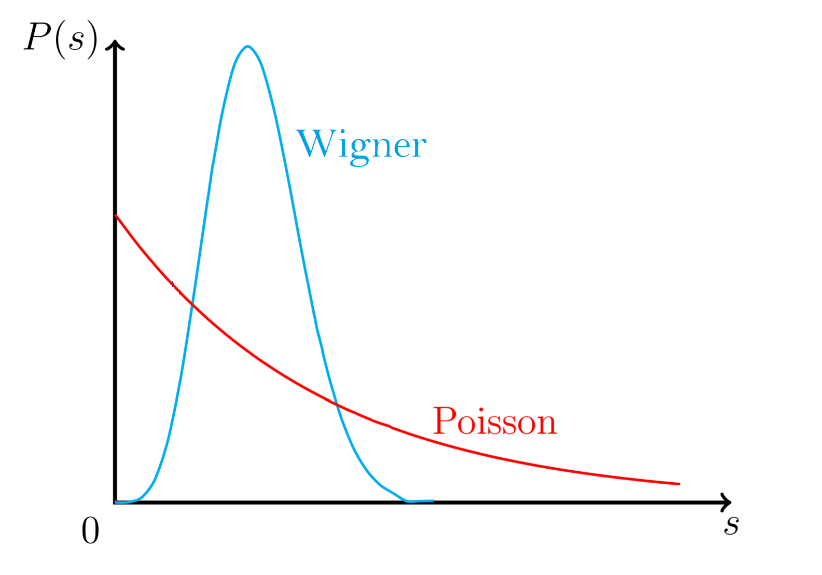
Afbeelding 3. Verschillende kansverdelingen.De Poissonverdeling vergeleken met Wigners verdeling.
Het blijkt dat de kansverdeling die volgt uit experimenten heel goed (tot op 1% nauwkeurigheid) kan worden benaderd met de kansverdeling gepostuleerd door Wigner. Wigners formule bleek dus heel mooi te werken.
Toevalsmatrices
De vraag is nu natuurlijk wat dit verhaal met matrices te maken heeft. Om deze vraag te beantwoorden moeten we beter begrijpen hoe Wigner aan zijn vermoedde verdeling is gekomen. We voegen om deze reden een extra element toe: we kijken niet naar gewone matrices, maar matrices die van het toeval afhangen – zogenaamde toevalsmatrices. Een toevalsmatrix is een tabel met getallen, waarbij de getallen in de matrix toevalsvariabelen zijn. Je kunt zo’n matrix zien als een grote dobbelsteen: iedere keer dat je met de dobbelsteen gooit, veranderen alle getallen in de matrix, maar je weet van tevoren niet welke getallen er komen te staan. Je kunt alleen iets zeggen over de kans dat ergens een bepaald getal komt te staan. Zo kunnen we bijvoorbeeld kijken naar toevalsmatrices waarbij de getallen in de matrix uit een zogeheten normale verdeling (met gemiddelde nul en standaardafwijking één) worden getrokken. Een voorbeeld van de uitkomst na een worp met zo’n `matrixdobbelsteen’ is hieronder gegeven:

We zien dat de meeste getallen dicht bij nul liggen, zoals je zou verwachten bij een normale verdeling (de kans hierop is immers het grootst).
Nu komt het verrassende: hoewel de getallen van een toevalsmatrix allemaal onafhankelijk van elkaar uit de kansverdeling worden getrokken, blijken de eigenwaarden van de matrix niet onafhankelijk te zijn. De grote verrassing is dat de kansverdeling die hoort bij de afstand tussen opeenvolgende eigenwaarden precies overeenkomt met Wigners vermoeden! In feite betekent dit dat het energiespectrum van een zware atoomkernen heel goed kan worden gemodelleerd door de eigenwaarden van een toevalsmatrix. We kunnen Wigners cruciale inzicht dus als volgt samenvatten: het ogenschijnlijk chaotisch gedrag van de energieniveaus van zware atomen kan misschien niet goed verklaard worden door een deterministische matrix – zoals bij het waterstofatoom – maar wel door een matrix die van het toeval afhangt.
Dit fundamentele inzicht – dat ogenschijnlijk chaotisch gedrag goed kan worden beschreven door de theorie van toevalsmatrices – heeft tot heel veel interessante ontdekkingen geleid. Naast atoomfysica blijken er namelijk nog enorm veel andere natuurkundige systemen te zijn waarvan het gedrag goed kan worden gemodelleerd door toevalsmatrices. In veel van deze gevallen is het nog steeds onbekend waarom de beschrijving in termen van toevalsmatrices zo goed werkt. Daar wordt op dit moment nog steeds actief onderzoek naar gedaan. Leuke voorbeelden zijn te vinden in quantumsystemen die klassiek chaotisch gedrag vertonen – zoals de baan van een quantumbiljartbal. Een ander verassend voorbeeld is dat bepaalde zwaartekrachtstheorieën in twee dimensies goed benaderd kunnen worden met toevalsmatrices. En zelfs de verdeling van de afstand tussen de nulpunten van de Riemann-zetafunctie – de hoofdrolspelers in de beruchte Riemann-hypothese – lijkt verdacht veel op de verdeling van de eigenwaarden van een toevalsmatrix. We zullen in de toekomst zeker nog een aantal artikelen wijden aan deze interessante toepassingen.
Kortom: de term `matrix’ heeft in de natuurkunde een heel andere betekenis dan in de gelijknamige film. Met alle ontdekkingen die sinds de afgelopen eeuw binnen de natuurkunde zijn gedaan – waarvan we er nu één hebben uitgeplozen – lijkt de term `matrix’ eigenlijk beter te passen bij de echte wereld dan bij de `schijnwereld’ waarin de film zich afspeelt.