
Afbeelding 1. Metronomen synchroniseren.Wanneer je de slinger van enkele metronomen laat bewegen terwijl de metronomen op een plankje ondersteund door twee blikjes staan, dan zullen de metronomen met eenzelfde frequentie gaan bewegen. Afbeelding uit dit YouTube-filmpje van Harvard Science Lecture Demonstrations.
Sommige QU-lezers zijn wellicht bekend met het fenomeen synchronisatie, door een vaak gedaan experiment waarbij metronomen op een plankje worden geplaatst dat zelf ondersteund wordt door lege blikjes; zie hier voor een filmpje op YouTube en afbeelding 1 voor een foto van de experimentele opstelling.
Wat je ziet gebeuren is opmerkelijk. De metronomen, die in de muziek worden gebruikt om een vast ritme aan te geven, worden ieder met een net wat ander ritme in trilling gebracht door de massa die op de slinger van de metronoom zit een klein beetje te verschuiven. Na enige tijd bewegen de metronomen met dezelfde frequentie en volledig in de pas. Dit fascinerende gedrag komt niet alleen voor in allerlei natuurkundige systemen, maar is ook in de biologie een frequent voorkomend verschijnsel. Denk bijvoorbeeld aan vuurvliegjes in Oost-Azië die met zijn allen licht uit zenden, waarbij het lijkt alsof ze van te voren hebben afgesproken wanneer ze precies hun achterlijf laten oplichten.
De verklaring is echter simpeler. Ook in dit geval is er synchronisatie aan het werk. De vuurvliegjes proberen de frequentie waarmee ze hun licht verspreiden af te stemmen op hun buren, waardoor ze uiteindelijk als een grote knipperlamp met zijn allen de omgeving doen oplichten en weer verduisteren. Andere voorbeelden van synchronisatie zijn zogenaamde alfagolven in de hersenen, waarbij de delen van de hersenen van een persoon met een frequentie van ongeveer 10 Hz oscilleren door koppelingen van de neuronen die zich daar bevinden; in de fysica vind je synchronisatie in supergeleiders met Josephson-juncties waarmee qubits kunnen worden gevormd die in de toekomst mogelijk in quantumcomputers hun weg vinden. Een andere toepassing van synchronisatie kent iedereen. De stroom die uit het stopcontact komt heeft bij iedereen in Europa een frequentie van 50Hz, terwijl deze stroom door heel veel verschillende generators wordt opgewekt. Ook hierbij speelt synchronisatie een erg belangrijke rol.
Gekoppelde systemen: een verklaring voor synchronisatie
Als we bovenstaande voorbeelden wat nader bekijken dan is er één eigenschap die ze gemeenschappelijk hebben. Alle synchroniserende systemen bestaan uit trillende, of oscillerende, eenheden die op de een of andere manier met elkaar gekoppeld zijn. Zo zijn de metronomen gekoppeld door het plankje op de blikjes. Dit kun je zien door de blikjes weg te halen, waardoor de synchronisatie snel zal verdwijnen. In de hersenen is er een koppeling tussen de verschillende neuronen die zonder koppeling met hun eigenfrequentie zouden oscilleren, maar die door de onderlinge interacties van de neuronen in het brein rond een gezamenlijke frequentie van ongeveer 10 Hz trillen.
Om te kunnen verklaren hoe die koppelingen tussen de verschillende oscillatoren leiden tot synchronisatie kunnen we een simpel model bestuderen dat voor het eerst door de Japanse fysicus Kuramoto is opgesteld en opgelost. Zijn idee was het volgende. Stel dat je een verzameling oscillatoren hebt die zonder interactie elk met een vaste natuurlijke frequentie trillen. We nemen aan dat die frequentie voor elke oscillator anders kan zijn en dat deze frequenties aan een willekeurige kansverdeling voldoen. Als deze oscillatoren vervolgens interactie met elkaar hebben dan zal die interactie zo moeten zijn dat de snellere oscillatoren de trage versnellen, terwijl de tragere oscillatoren de snelle juist vertragen, om ervoor te zorgen dat ze met dezelfde frequentie gaan bewegen. Dit kunnen we het gemakkelijkst illustreren door naar een cirkel te kijken en elke oscillator te zien als een deeltje dat op een eenheidscirkel ronddraait met een karakteristieke frequentie.
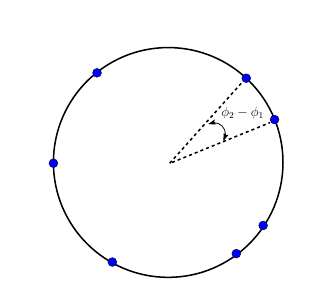
Affbeeding 2. Een model voor synchronisatie.Elke oscillator beweegt tegen de klok in met een bepaalde snelheid. De interactie tussen alle oscillatoren wordt gegeven door de formule in het artikel en hangt alleen af van de afstand tussen de deeltjes gemeten langs de cirkel.
De interactieterm die de wisselwerking tussen twee deeltjes weergeeft kiezen we als een sinus van het verschil tussen de hoeken die deze deeltjes met de x-as maken, ofwel de sinus van de afstand gemeten langs de eenheidscirkel. Dit kan als volgt worden opgeschreven:
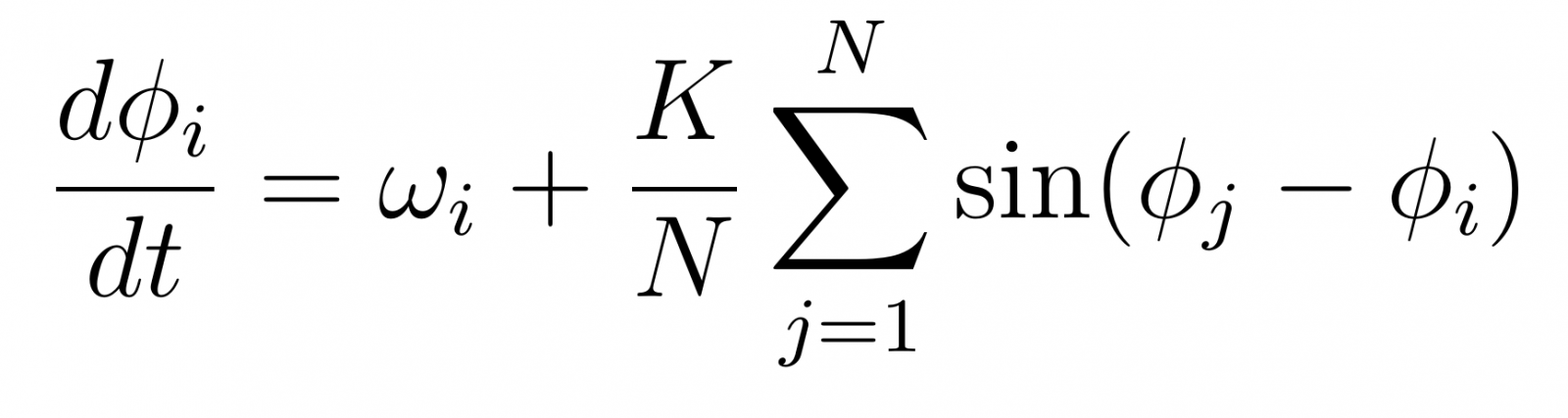
In deze vergelijking staat links de snelheid waarmee de oscillatoren zich over de cirkel verplaatsen en rechts de factoren waardoor deze snelheid wordt beïnvloed: de eigenfrequentie van de oscillatoren, ωi, en de koppeling met alle andere oscillatoren. Merk op dat deze interactie inderdaad doet wat we wilden: langzaam bewegende oscillatoren versnellen (dan wordt de sinus van de hoeken met de andere deeltjes steeds groter) en snellere oscillatoren vertragen (dan wordt de sinus juist steeds kleiner). De sterkte van de koppeling wordt aangeven door koppelingsconstante K. Deze constante wordt in de formule gedeeld door het aantal oscillatoren, omdat er wisselwerking is met elke oscillator en anders de totale sterkte van de koppeling enorm zou worden voor veel oscillatoren.
De oplossing van Kuramoto
Om het hierboven beschreven model op te lossen – dat wil zeggen: uit te vinden hoe de verschillende deeltjes uiteindelijk bewegen – gebruikte Kuramoto een truc. Hij introduceerde een zogenaamde ordeparameter, een techniek die vaker wordt gebruikt in de statistische fysica, die systemen met veel deeltjes beschrijft, zoals gassen en vaste stoffen. Deze ordeparameter beschrijft hoe het systeem zich op macroscopisch niveau gedraagt. In het geval van magnetisme is de ordeparameter bijvoorbeeld de gemiddelde magnetisatie van het materiaal. In het Kuramoto model kan het gemiddelde van de fasehoeken van alle oscillatoren als ordeparameter dienen. Als alle hoeken hetzelfde zijn is de ordeparameter, vaak aangeduid met R, gelijk aan 1 en als de hoeken willekeurig verdeeld zijn, dan is R=0. Door het gebruik van de ordeparameter R, kan de vergelijking voor de hoeken (1) worden opgelost en hieruit wordt dan weer het gedrag van de ordeparameter R bepaald. Het mooie hiervan zie je wanneer je kijkt naar hoe de ordeparameter zich gedraagt. Voor grote koppelingen is R inderdaad ongeveer 1, dus het systeem is gesynchroniseerd, terwijl voor kleine waarden van K geen synchronisatie optreedt. Dit wordt ook geschetst in afbeelding 3.
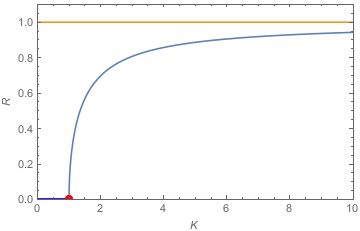
Afbeelding 3. De ordeparameter.De ordeparameter R als een functie van de koppelingssterkte K (blauw). Je ziet duidelijk een transitie bij de rode punt. Als K groter wordt dan deze drempelwaarde dan neemt de synchronisatie snel toe naar de maximale waarde R=1 Het precieze verloop van de curve en het transitiepunt zelf hangt af van hoe de eigenfrequenties precies verdeeld zijn.
Al met al kunnen we zeggen dat synchronisatie een belangrijke rol speelt in veel toepassingen, variërend van biologisch tot toepassingen op elektriciteitsnetwerken en dat het verschijnsel in termen van een relatief simpel model kan worden begrepen. Behalve de hier besproken verschijnselen zijn er nog veel meer synchronisatie-gerelateerde verschijnselen (denk bijvoorbeeld aan applaus in een menigte) en kan synchronisatie ook gebruikt worden om bijvoorbeeld structuren van netwerken te achterhalen. Dit komt omdat alleen gekoppelde oscillatoren kunnen synchroniseren. Door nu op synchronisatie in het netwerk te letten, is het mogelijk bepaalde gekoppelde clusters te identificeren en zo dus de netwerkstructuur gedeeltelijk te onthullen. Voor iedereen die nog meer over synchronisatie wil weten is er het boekje Sync van Steven Strogatz [1], die daarin verscheidene wiskundige aspecten van synchronisatie erg duidelijk belicht.
[1] S. Strogatz, Sync: How Order Emerges from Chaos in the Universe, Nature, and Daily Life.