
Afbeelding 1. Symmetrie.Symmetrie is vaak in de natuur aanwezig. Maar wanneer is iets supersymmetrisch? Foto: Andrew Hurley (CC BY-SA 2.0).
Bosonen en fermionen
In de natuur blijken er op fundamentele schaal twee typen deeltjes te bestaan. Aan de ene kant heb je de bosonen, vernoemd naar Satyendra Nath Bose. Als bekendste voorbeeld van de elementaire deeltjes geldt het foton, het deeltje geassocieerd met licht. Het Higgs-boson is, zoals zijn naam doet vermoeden, de meest recente aanwinst voor deze groep van deeltjes. Aan de andere kant heb je de fermionen, vernoemd naar Enrico Fermi, zoals het elektron, de quarks en de neutrino’s. Deze deeltjes spelen zeer verschillende, maar belangrijke rollen in de natuur.
De bosonen zijn de deeltjes die verantwoordelijk zijn voor het overbrengen van de fundamentele krachten. Een karakteristieke eigenschap is dat ze op grote schaal collectief gedrag kunnen vertonen, zoals bijvoorbeeld wanneer vele fotonen van eenzelfde frequentie samen een laserstraal vormen. Ook de zogeheten Bose-Einsteincondensatie is een extreem voorbeeld van dit collectieve gedrag.
Het zijn de fermionen die door de krachten die door bosonen worden overgebracht tot elkaar aangetrokken of door elkaar afgestoten worden en op die manier de basis vormen voor al de aan ons bekende materie. Je kunt zeggen dat fermionen veel individualistischer zijn dan de bosonische kuddedieren. Fermionen kunnen fundamenteel niet in eenzelfde toestand zitten, wat in de natuurkunde ook wel bekend staat als het uitsluitingsprincipe van Pauli. Deze definiërende eigenschap heeft onder andere tot gevolg dat de elementen in het periodiek systeem allemaal wonderlijk verschillende eigenschappen hebben. Dat zit zo: omdat de fermionen niet in eenzelfde toestand mogen zitten, moeten zij zich in steeds ingewikkeldere bochten wringen om toch allemaal in een atoom te passen. De wetenschappelijke benaming voor deze `bochten’ is elektronenschillen. Je kunt je die voorstellen als steeds ingewikkeldere geometrische banen die rond de atoomkern zijn opgebouwd.

Afbeelding 2. Bose en Fermi.Satyendra Nath Bose (1894-1974) en Enrico Fermi (1901-1954). Foto links: auteur onbekend. Foto rechts: nobelprize.org.
Een onverwachte symmetrie
Het zal je misschien verrassen dat er een symmetrie kan bestaan tussen deze twee typen deeltjes. Toch werd deze symmetrie in de jaren 50 en 60 in theoretische modellen ontdekt. Een van de eerste plekken was in de snaartheorie. Supersymmetrie bleek namelijk een noodzakelijk theoretisch concept om fermionen vanuit het perspectief van een snaar te kunnen beschrijven. Als snaartheorie een kans zou willen maken om elektronen en quarks te beschrijven, dan is er geen ontkomen aan supersymmetrie! Na deze ontdekking heeft een goed gedeelte van de theoretische natuurkundigen zich langzaam maar zeker gestort op het bestuderen van het fenomeen supersymmetrie buiten de snaartheorie, toegepast op quantumveldentheorie-modellen zoals het standaardmodel.
Deze supersymmetrische modellen hebben als kenmerkende eigenschap dat er voor ieder fermion een boson bestaat en vice versa. Er is voor het elektron bijvoorbeeld een partnerdeeltje, het selektron, dat precies dezelfde dezelfde eigenschappen als het elektron heeft: dezelfde massa en dezelfde elektrische lading, bijvoorbeeld. Het enige (en grote) verschil tussen de twee deeltjes is dat het selektron een bosonisch in plaats van fermionisch karakter heeft. Als onze wereld supersymmetrisch zou zijn, dan zouden er naast onze normale atomen ook nieuwe superatomen bestaan, die uit de partners van elektronen en protonen zijn opgebouwd. Deze atomen zouden zich chemisch gezien radicaal anders gedragen dan hun normale partners, aangezien bosonen zich zo anders gedragen dan fermionen. Ook zouden er gemixte atomen kunnen bestaan, die zowel uit de gewone deeltjes als hun superpartners bestaan.
Er bestaan ook toestanden die een gedeelte van de supersymmetrie breken. Dit zijn zogeheten BPS-toestanden, en een beroemd voorbeeld is een klasse van magnetische monopolen. De manier waarop deze toestanden een gedeelte van de supersymmetrie breken is goed te vergelijken met de manier waarop een gemagnetiseerde toestand van een metaal een gedeelte van de draai-symmetrie breekt. De losse “mini-magneetjes” in een metaal kunnen in principe alle verschillende kanten op wijzen – er is dus een draaisymmetrie waardoor alle richtingen gelijkwaardig zijn. In een gemagnetiseerd stuk metaal hebben de magneetjes echter een bepaalde richting gekozen. De richting van het ontstane magneetveld, zeg in de z-richting van een (x,y,.z) assenstelsel, breekt dus de draaisymmetrie: de magneet is niet meer symmetrisch onder alle driedimensionale draaiingen, maar nog wél onder draaiingen om de z-as.
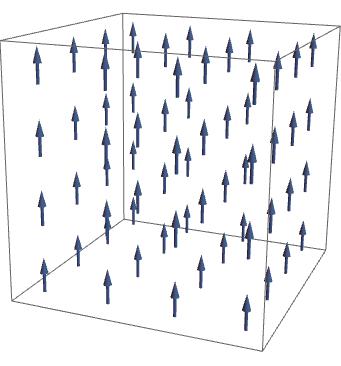
Afbeelding 3. Een magneet.Een magneet ontstaat als alle magnetische bouwstenen van een metaal in één richting wijzen. De draaisymmetrie is dan deels gebroken: alleen draaiing rond de z-as laat in dit voorbeeld de configuratie onveranderd.
Het moge duidelijk zijn dat supersymmetrie zoals ik die hierboven heb beschreven, zeker niet een eigenschap is van de wereld om ons heen. Ten eerste zou de grote lading aan nieuwe deeltjes, een “spiegelbeeld” van het standaardmodel, allang in een van de talloze deeltjesexperimenten gevonden moeten zijn. De conlusie is dan ook dat supersymmetrie op zijn minst in onze wereld een gebroken symmetrie is – net als in het voorbeeld van de magneet hierboven, waarin we bepaalde symmetrieën niet meer “zien” – of, op zijn ergst, dat het simpelweg geen directe toepassing heeft op onze natuur.
Waarom is het dan interessant?
Ik zal in het laatste stuk van dit artikel aan de hand van een aantal motivaties schetsen waarom er toch een groot aantal wetenschappers hun levens hebben gewijd aan het uitwerken van deze eigenaardige symmetrie. Er zijn meerdere motivaties, en welke je voorgeschoteld krijgt hangt sterk af van de persoon aan wie je het vraagt. De volgende redenen zijn dus persoonlijk en afkomstig van een snaartheoreet.
Zoals eerder genoemd is er vanuit de snaartheorie een indirecte motivatie voor het bestuderen van supersymmetrie. Snaartheorie is namelijk nog steeds een serieuze kandidaat om een theorie van quantumzwaartekracht te beschrijven. En supersymmetrie blijkt een cruciaal onderdeel van snaartheorie.
Ook zou het bestaan van supersymmetrie bewijsmateriaal leveren voor een stelling, de zogeheten grote unificerende theorie (GUT), dat de drie microscopische krachten in de natuur (de sterke kernkracht, de zwakke kernkracht en de electromagnetische kracht) allemaal hun oorsprong vinden in een enkele natuurkracht. Men kan namelijk met berekeningen nagaan dat de sterktes van deze krachten, ook wel de koppelingsconstantes genoemd, op een zeer hoge energieschaal aan elkaar gelijk worden in het geval dat de natuur supersymmetrisch is! Deze hoge energieschaal wordt ook wel de GUT-schaal genoemd, en bedraagt 1025 eV. Ter vergelijking: er worden nu plannen gemaakt voor een nieuwe deeltjesversneller die over 20 jaar misschien zo’n 1014 eV kan bereiken – nog altijd elf factoren 10 lager dan de GUT-schaal! Leptonen, zoals het elektron en zijn broertjes, het muon en het tauon, worden in zo’n GUT samengenomen met de quarks tot een enkel object dat ik bij gebrek aan fantasie maar even een “lepquark” noem. Dit zou onder meer verklaren waarom er zowel drie families van leptonen als van quarks bestaan.
Supersymmetrie wordt ook vaak genoemd als een oplossing van het hiërarchieprobleem. Dit probleem laat zich zeer bondig samenvatten tot de vraag: waarom is zwaartekracht zoveel zwakker dan de zwakke kernkracht? Een groot vraagteken dat hieraan gelinkt is, is waarom het Higgsdeeltje relatief licht is. Vanuit het standaardmodel zelf is dit (vooralsnog) niet te begrijpen, maar met een supersymmetrische extensie van het standaardmodel zou dit laatste aspect van het probleem worden opgelost.

Afbeelding 4. Een bolvormige koe.Een bolvormige koe is minder realistisch dan een echte, maar eraan rekenen is wel veel eenvoudiger! Afbeelding: Nepluno (CC BY-SA 4.0).
Een laatste en meer algemene motivatie is het zogenaamde “bolvormige koe-principe”, dat ik als volgt kan uileggen. Theoretisch natuurkundigen houden ervan om problemen exact op te lossen in plaats van een benadering te maken, omdat een exacte oplossing nu eenmaal meer inzicht biedt. Dit is typsich alleen mogelijk als de ingrediënten in het probleem simpel genoeg zijn. De aanwezigheid van een hoge mate van symmetrie levert vaak zo’n simplificatie op. Het blijkt dat supersymmetrie een symmetrie is die veel meer exacte berekeningen toestaat dan wanneer er geen supersymmetrie in het probleem aanwezig is. De truc is dan om een supersymmetrisch model te bouwen dat zoveel mogelijk op zijn minder symmetrisch maar meer realistische neefje lijkt, zoals een bolvormige koe op een koe kan lijken, maar qua rekenwerk (bijvoorbeeld om zijn inhoud te bepalen) een stuk eenvoudiger is. De hoop is dat sommige aspecten van de analyse in het meer symmetrische model ook overeind blijven in gevallen dat er geen supersymmetrie is. Op die manier kunnen we met behulp van supersymmetrische modellen toch iets leren over onze eigen natuur, of die nu supersymmetrisch is of niet.