
Afbeelding 1. Een (dubbele) regenboog.Bij deze regenboog is heel duidelijk te zien dat de lucht aan de binnenkant lichter is dan aan de buitenkant – een gevolg van Stokes’ fenomeen. Foto: Goodfreephotos.
Asymptotisch gedrag
Natuurkundige vraagstukken zijn zelden wiskundig exact op te lossen. Dat is niet omdat natuurkundigen niet slim genoeg zijn, maar omdat de gebruikelijke gereedschapskist aan wiskundige functies – machten, sinussen, logaritmes, noem maar op – gewoonweg niet voldoende verschillende uitdrukkingen bevat om elke mogelijke natuurkundige situatie te beschrijven. Dat probleem kan al heel snel ontstaan: laat bijvoorbeeld drie planeten onder invloed van elkaars zwaartekracht hun baantjes draaien, en de positie van een planeet als functie van de tijd zal in het algemeen al niet meer een functie zijn die in de wiskundeboeken staat.
Natuurlijk is dergelijk “onbeschrijfbaar gedrag” geen onoverkomelijk probleem. Ten eerste kunnen we het gedrag van natuurkundige systemen vaak met allerlei slimme trucs in onze wiskundige beschrijving wel willekeurig dicht benaderen, en ten tweede zijn we vaak niet geïnteresseerd in het exacte gedrag van een systeem op elke willekeurige plaats en op elk willekeurig moment. Geef een klap tegen een tennisbal, en het zal je niet heel veel interesseren welke snelheid de bal na 0,37 seconden heeft. Wat je wilt weten is waar de bal uiteindelijk terechtkomt, en met welke snelheid.
Kortom: vaak zijn we in de natuurkunde vooral geïnteresseerd in wat asymptotisch gedrag heet: hoe ziet de oplossing van ons systeem eruit na lange tijd, of in een bepaalde richting? Wiskundiger geformuleerd: hoe gedraagt de oplossing zich als een bepaalde coördinaat heel groot wordt? Het mooie is nu dat zulk asymptotisch gedrag vaak wél heel goed te benaderen is met bestaande functies: als je maar lang genoeg wacht, of ver genoeg weg kijkt, gedragen veel natuurkundige systemen zich opeens heel “netjes”.

Afbeelding 2. George Gabriel Stokes (1819-1903).Foto ca. 1860, fotograaf onbekend.
Welke richting?
Wat asymptotisch gedrag in de tijd betreft zijn er natuurlijk altijd maar twee situaties van belang: hoe gedroeg de oplossing zich in een ver verleden, en hoe gedraagt ‘ie zich in de verre toekomst? Waar komt de meteoriet die vandaag inslaat precies vandaan? Wat zal, als we niets aan het broeikaseffect doen, het gevolg zijn voor de temperatuur op aarde over lange tijd?
Voor asymptotisch gedrag met betrekking tot de richting is de situatie veel interessanter, want er bestaat natuurlijk een oneindig aantal mogelijke richtingen. Als een meteoriet in de oceaan inslaat, kun je je afvragen wat de gevolgen ver in het noorden zijn, of ver in het westen, maar ook in het noordwesten, of 28,3 graden westelijk van het noorden.
Nu zou je in eerste instantie misschien verwachten dat die informatie op een “gladde” manier van de richting afhangt. Als je de waterhoogte ver in het noorden en die ver in het westen weet, dan zal de waterhoogte ver in het noordwesten daar wel ergens tussenin zitten, toch? Vaak is dat inderdaad het geval, maar wat de Ierse wis- en natuurkundige George Stokes halverwege de 19e eeuw ontdekte was dat er ook interessante uitzonderingen op die regel zijn!
Stokes’ fenomeen
Eén mogelijke manier waarop een functie zich kan gedragen als een bepaalde coördinaat groot wordt is bijvoorbeeld exponentieel: als de functie ex. Deze functie groeit heel snel: zie de grafiek links in afbeelding 3 hieronder. Natuurlijk kan een functie juist ook exponentieel afnemen: dan gedraagt die functie zich asymptotisch als e-x, de functie in de rechtergrafiek in afbeelding 3. In zekere zin horen deze twee gedragingen bij elkaar: als een functie bijvoorbeeld naar rechts toe exponentieel toeneemt, ligt het voor de hand dat diezelfde functie naar links toe exponentieel zal afnemen.
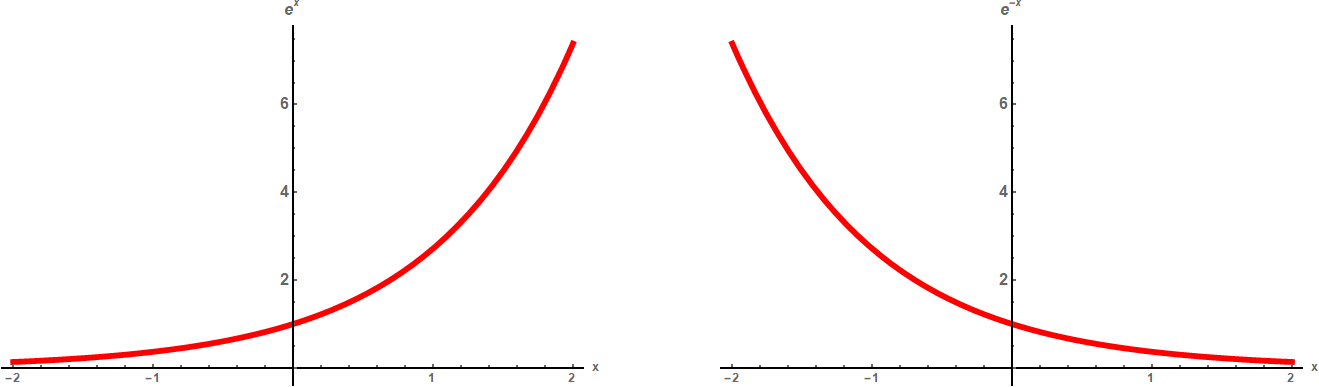
Afbeelding 3. Exponentiële functies.Links: de exponentieel groeiende functie ex. Rechts: de exponentieel afnemende functie e-x.
Er bestaat een bekende relatie tussen exponentiële functies en de sinus- en cosinusfuncties:
![]()
In deze relatie komt het complexe getal i voor (zie deze driedelige serie voor veel meer over complexe getallen), maar wat voor ons verhaal belangrijker is: we kunnen de sinus- en de cosinusfunctie dus zien als combinaties van twee exponentiële functies. De sinus- en cosinusgrafieken zien er ook heel anders uit dan de exponentiële grafieken:
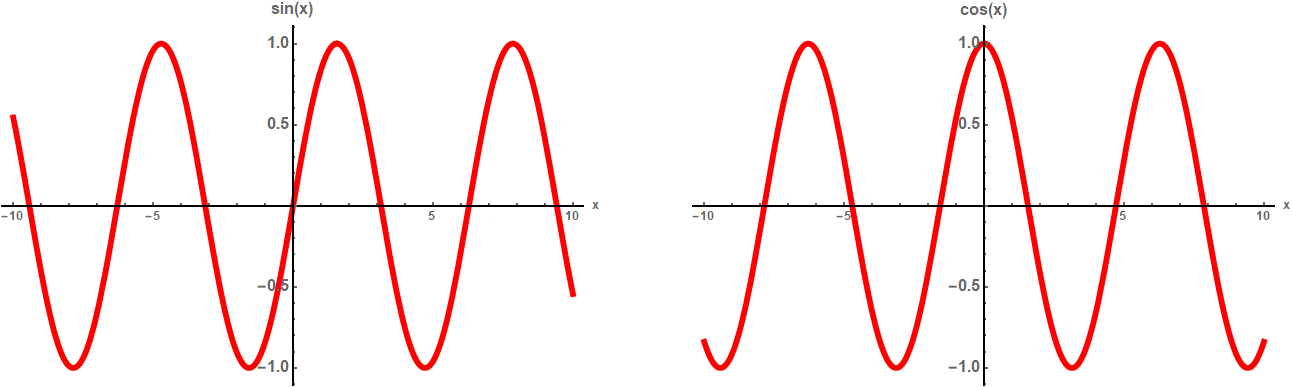
Afbeelding 4. Sinus- en cosinusfuncties.Links: de functie sin(x). Rechts: de functie cos(x).
Omdat de sinus en cosinus bestaan uit twee exponentiële functies, zou je niet verwachten dat een functie die zich in één richting exponentieel gedraagt, zich in een andere richting gedraagt als een sinus of een cosinus. Immers: als het probleem zelf “glad” is – als de vergelijkingen die je oplost geen “sprongen” vertonen – zou je hooguit verwachten dat één exponentiële functie als ex geleidelijk verandert in één andere exponentiële functie zoals eix, maar niet dat er “uit het niets” nog een tweede exponentiële functie zoals e-ix bijkomt!
Wat Stokes ontdekte, was dat dit verrassende gedrag toch kan optreden. Zelfs als het natuurkundige probleem volkomen “glad” is, kan het in de oplossing gebeuren dat het asymptotische gedrag voor een groot bereik aan richtingen het ene gedrag vertoont, en dan vervolgens opeens “springt” naar een heel ander asymptotisch gedrag!
De regenboog
Het bekendste voorbeeld van Stokes’ fenomeen – en ook het voorbeeld dat Stokes zelf bestudeerde – is de lichtintensiteit rond een regenboog. Het blijkt dat die intensiteit beschreven wordt door een functie die de Airy-functie heet, genoemd naar een andere negentiende-eeuwse wetenschapper, de Brit George Airy. Hieronder zie je een grafiek van de Airy-functie:
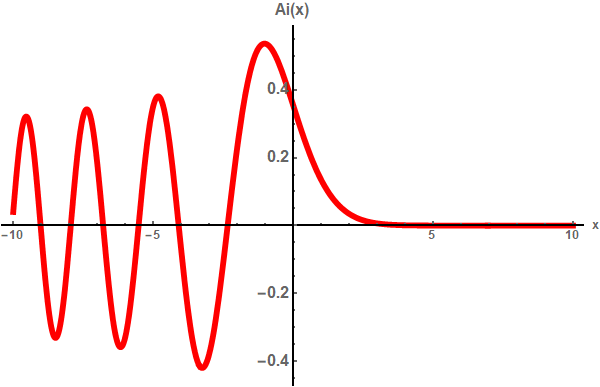
Afbeelding 5. De Airy-functie.Links gedraagt de Airy-functie zich als een sinus; rechts als een afnemende e-macht.
Misschien valt je op dat deze functie precies het verrassende gedrag heeft dat we hierboven bespraken: in de ene richting neemt de functie exponentieel af; in de andere richting golft de functie zoals een sinus. Dit is Stokes’ fenomeen in actie: in de ene richting hebben we maar één exponentiële functie nodig om het asymptotische gedrag te beschrijven; in de andere richting komt daar opeens een tweede (complexe) exponentiële functie bij en krijgen we een sinus.
Het golfgedrag in de lichtintensiteit van een regenboog is overigens in de praktijk niet eenvoudig te zien. In simulaties gaat dat beter: hieronder zie je een dergelijke simulatie.

Afbeelding 6. Een gesimuleerde regenboog.Onder de regenboog is goed te zien dat de lichtintensiteit sinusvormig toe- en afneemt. Simulatie gemaakt met de Airy Rainbow Simulator.
Wat vaak wél heel duidelijk te zien is is het exponentiële verval in de andere richting: als je goed kijkt, zie ze dat de lucht aan één kant van de regenboog altijd wat donkerder is dan aan de andere kant – zie bijvoorbeeld de foto bovenaan dit artikel, waar dit heel duidelijk te zien is. Let er volgende keer vooral eens op als je een regenboog ziet, en bedenk je dan dat je kijkt naar iets wat in de wiskunde een heus “fenomeen” heet!