Niets… is toch iets!
Laten we de bovenstaande vraag iets preciezer maken. Kunnen we een rotatie van 360 graden langzaam vervormen tot een rotatie van 0 graden? Neem om die vraag te beantwoorden twee potloden, en verbind ze met een strook papier – zo ongeveer als in afbeelding 1a hieronder.
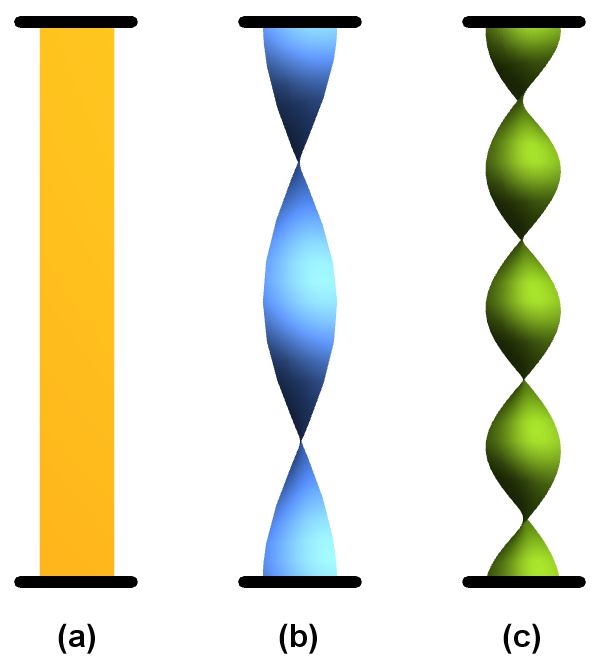
Afbeelding 1. Rotaties.Twee potloden verbonden door een strook papier. De plaatjes geven de eindsituatie weer als we het onderste potlood draaien over een hoek van (a) 0 graden, (b) 360 graden en (c) 720 graden.
Als we de potloden en de strook papier strak recht houden, heeft de strook papier overal een draaiing van 0 graden. Nu houden we het onderste potlood in zijn oorspronkelijke positie, en draaien we het bovenste 360 graden rond de verticale as. Het eindresultaat ziet eruit zoals in afbeelding 1b. De strook papier geeft een mooie weergave van de gehele draaiing die we zojuist hebben uitgevoerd: de draaiing in de strook verloopt langzaam van 0 graden tot 360 graden rond de verticale as als we langs de strook omhoog bewegen.
De vraag is nu: kunnen we deze draaiing “vervormen” tot een draaiing waarin helemaal niets gebeurt? Met andere woorden: kunnen we de potloden in dezelfde positie houden maar de strook papier zo bewegen dat het eindresultaat eruitziet als in afbeelding 1a? Probeer dit vooral zelf! (Als je dit probeert, beweeg dan gerust de potloden wat door de ruimte om meer bewegingsruimte te hebben, maar verander natuurlijk niet de richting waarin ze wijzen!)
Wie dit probeert, zal er al snel achter komen dat het niet lukt om de situatie in afbeelding 1b te vervormen tot de situatie in afbeelding 1a. Hoewel de toestand (de oriëntatie van de potloden) er onderaan en bovenaan exact hetzelfde uitziet, is de gehele rotatie (weergegeven door de strook papier) bij “0 graden draaien” en “360 graden draaien” niet hetzelfde!
Tweemaal iets… is niets?
“Logisch”, zul je misschien denken, maar nu komt het bijzondere. Herhaal nu het experiment, maar draai het bovenste potlood tweemaal rond, dus draai het 720 graden om de verticale as. Nu ziet het resultaat eruit als in afbeelding 1c. Kunnen we nu de totale draaiing vervormen tot een draaiing die overal 0 graden is? Het verrassende antwoord: ja, dat kan! Probeer het vooral weer zelf! In onderstaande video zie je twee leuke manieren waarop dit resultaat gedemonstreerd wordt:
“Ho, stop!”, zul je nu misschien zeggen. Om de strook papier (of, zoals in de video hierboven, het haar) weer “vlak” te krijgen, moet je die strook over het potlood heen tillen. Is dat wel toegestaan?
Laten we nog eens goed kijken naar wat er gebeurt als je de strook papier over het potlood heen tilt. De strook papier blijft natuurlijk een continu geheel, maar je zult zien dat bij deze beweging een aantal van de orrspronkelijk horizontaal lopende doorsnedes van het papier tijdelijk verticaal komen te staan. Met andere woorden: we kunnen “720 graden draaien” wel vervormen tot “0 graden draaien”, maar niet op zo’n manier dat onderweg alle draaiingen in hetzelfde platte vlak blijven liggen. Iets wiskundiger geformuleerd: met alleen draaiingen in twee dimensies kun je “720 graden draaien” niet vervormen tot “0 graden draaien”, maar met draaiingen in drie dimensies kan dat wel.
We zijn daarmee dus gestuit op een bijzondere eigenschap van draaiingen in drie dimensies, die niet geldt voor draaiingen in twee dimensies. Als we een voorwerp 360 graden draaien kunnen we die beweging niet “terugvervormen” tot een draaiing van 0 graden, maar als we het voorwerp twee keer (of elk ander even aantal maal) 360 graden draaien kan dat wel. De “trucs” om dat te laten zien, zoals hierboven in het filmpje, worden meestal toegeschreven aan de bekende quantumfysicus Paul Dirac. Hieronder nog een mooie animatie van Jason Hise die hetzelfde idee weergeeft:
Natuurkunde?
Dit lijkt een leuk wiskundig weetje, maar heeft het ook iets met natuurkunde te maken? Het feit dat het Paul Dirac was die de bovenstaande trucs verzon, doet natuurlijk vermoeden van wel. Wat het wiskundige weetje ons laat zien, is dat voorwerpen in drie dimensies na 360 graden draaien niet noodzakelijk hetzelfde hoeven te zijn als voordat we ze draaien – die wiskundige noodzaak is er pas na 720 graden draaien. Zouden zulke bizarre voorwerpen in de natuur bestaan? Dat is inderdaad het geval: er blijken op quantumniveau in de natuur elementaire deeltjes voor te komen die, als we ze 360 graden draaien, niet exact hetzelfde zijn als in hun oorspronkelijke toestand. Pas als we deze deeltjes 720 graden ronddraaien, zijn al hun quantumeigenschappen (iets preciezer: is hun golffunctie) weer exact hetzelfde als voor de draaiing.
Dergelijke deeltjes worden fermionen genoemd. Lees vooral ons dossier over quantummechanica als je meer wilt weten over fermionen, golffuncties en spin – de eigenschap die het gedrag beschrijft van deeltjes als we ze ronddraaien.
Een leuke bijkomende eigenschap van fermionen is de volgende. Neem twee exact identieke potloden, en verwissen die van plaats. De eindtoestand ziet er dan precies uit als de begintoestand. Maar ook hier kunnen we ons afvragen: kunnen we deze uitvoering van de “identiteit” ook vervormen tot een proces waarin de hele tijd niets gebeurt? Met één verwisseling blijkt dit niet te kunnen, maar met twee verwisselingen weer wel. En inderdaad: ook fermionen vertonen dit gedrag: als we twee exact dezelfde fermionen verwisselen is de toestand niet hetzelfde als daarvoor. Een gevolg daar weer van is dat het dus uitgesloten is dat twee fermionen op precies dezelfde plaats in precies dezelfde toestand kunnen zijn – dan zou de toestand immers wél symmetrisch zijn onder verwisseling. Uit hun eigenschappen onder draaiingen volgt dus dat fermionen “hard” zijn: ze kunnen niet door elkaar heen bewegen! Alle “harde” elementaire deeltjes in de natuur – elektronen, bijvoorbeeld – zijn dan ook fermionen. Voor “zachte” deeltjes, zoals lichtdeeltjes (fotonen) die door elkaar kunnen bewegen, geldt dat niet.
Dat deeltjes na twee keer verwisselen wel altijd in dezelfde toestand terugkeren, kun je ook weer met een soortgelijke “belt trick” als die van Dirac laten zien. Zie deze Vimeo-video van Antonio Martes de la Torre voor een voorbeeld daarvan.