Lichtkegels en speciale relativiteit
Laten we beginnen met de vraag hoe de beweging van deeltjes volgens de speciale relativiteitstheorie handig beschreven kan worden. De wetten van Einstein vertellen ons dat normale deeltjes niet sneller dan het licht kunnen bewegen. In het beste geval, wanneer een deeltje massaloos is, beweegt het voort met de lichtsnelheid. Om dit grafisch duidelijker te maken, kunnen we de tijd \( t \) van het deeltje uitzetten tegen zijn positie \( x \) . Als we de lichtsnelheid voor het gemak symbolisch op \( c=1 \) zetten, betekent dit dat licht in het plaatje in de diagonale richtingen onder 45 graden beweegt — het afleggen van bijvoorbeeld een lichtseconde (de afstand die licht in een seconde aflegt) duurt dan precies één seconde.
Omdat de deeltjes die wij tot nog toe kennen niet sneller dan het licht bewegen, kunnen we deze diagonale lijnen zien als een scheidslijn. Nemen we meer dan één richting in de ruimte in ons plaatje mee, dan vormen de mogelijke banen van het licht samen geen V-vorm meer maar een kegel. Binnen deze kegel kunnen punten door signalen vanuit de oorsprong bereikt worden, terwijl plekken daarbuiten in principe vanuit de oorsprong onbereikbaar zijn. Punten binnen elkaars lichtkegel noemen we daarom ook wel causaal verbonden.

Voordat we naar het gedrag van tachyonen kijken, is het nuttig om eerst te kijken naar de energie van normale deeltjes. Volgens de wetten van de speciale relativiteit volgt deze energie \( E \) uit
\( E^2 = \frac{m^2}{1-v^2} \),
waarbij \( m \) de massa en \( v \) van het deeltje is. Je kunt deze relatie zien als de relativistische versie van het bekendere \( E = \frac12 m v^2 \). Voor onze doeleinden is het nuttig om deze formule om te schrijven in termen van de impuls van het deeltje. In de klassieke mechanica volgt de impuls uit de snelheid van het deeltje als \( p = m v\), maar voor hogere snelheden, als de relativiteitstheorie een rol gaat spelen, is ook deze relatie iets ingewikkelder. Het verband tussen energie en impuls is echter wel weer betrekkelijk eenvoudig: de energie kan geschreven worden als
\( E^2 = m^2+p^2 \).
Voor een deeltje dat stilstaat, oftewel \( p=0 \), herkennen we de bekende vergelijking \( E = m c^2 \) (met \( c=1 \) in onze eenheden) terug.
Vervolgens kunnen we de energie van een deeltje uitzetten tegen zijn impuls. Voor deeltjes zoals lichtdeeltjes die massaloos zijn, \( m=0 \), vinden we opnieuw twee diagonale lijnen \( E = \pm p \). Voor deeltjes met massa is de formule iets ingewikkelder, namelijk \( E = \sqrt{ m^2 + p^2} \), maar kunnen we de relatie nog steeds schetsen. Dit geeft een hyperbool (blauw) die de E-as snijdt op \( E = m \), precies zoals we eerder vonden. We zien hierin ook dat we, hoe groot we de impuls van het deeltje ook maken, alleen maar de lijn van de lichtsnelheid kunnen benaderen, en nooit doorkruisen.
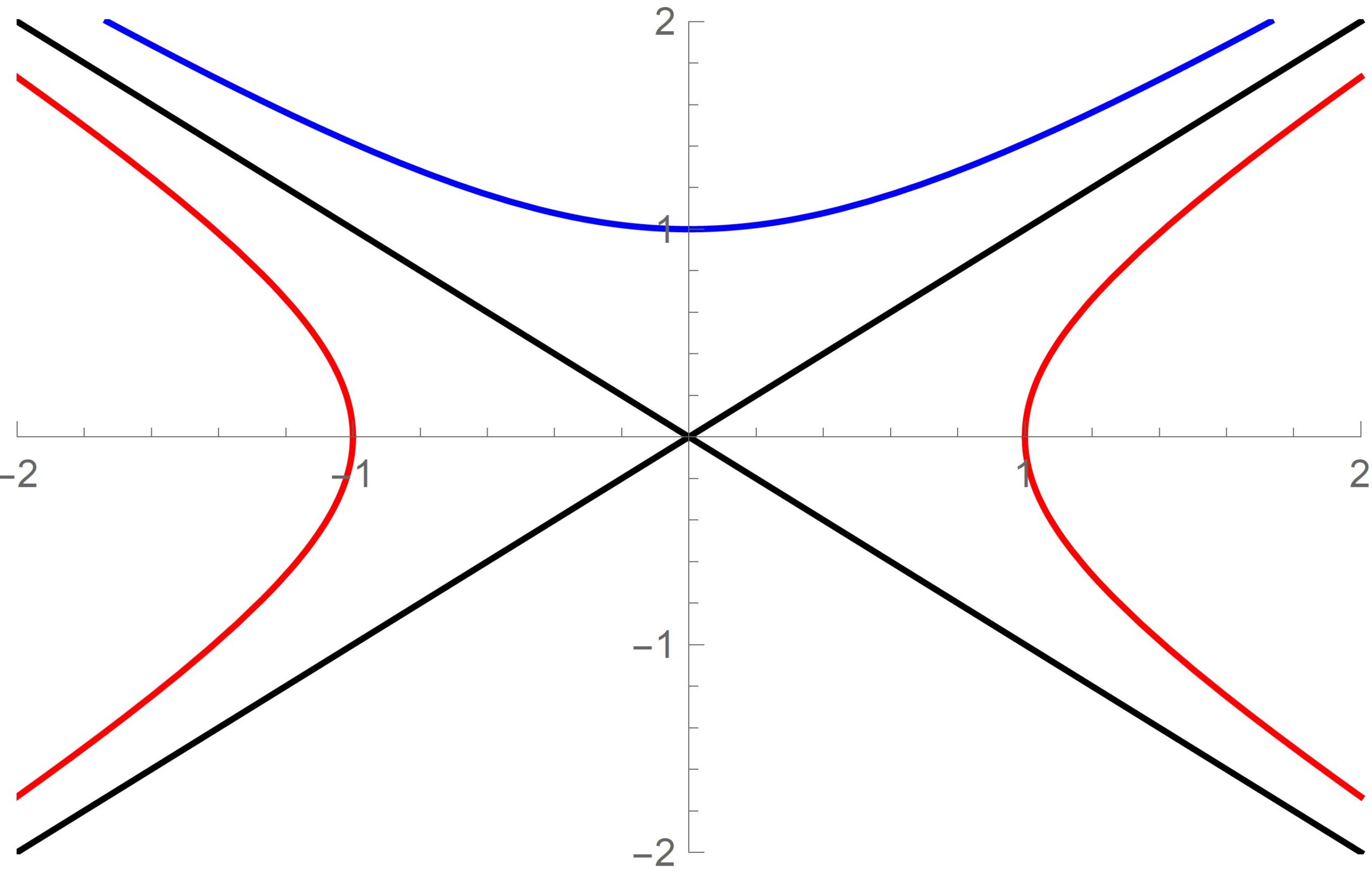
Een logische vervolgstap is nu om soortgelijke hyperbolen te tekenen in de kwadranten aan de linker- en rechterkant (rood), en te kijken of deze ook een fysische betekenis hebben. Deze hyperbolen worden ook gegeven door \( E =\pm \sqrt{ m^2 + p^2}, maar nu met \) met \( m^2 <0 \) negatief. En wat blijkt nu: dit zijn precies de krommen die tachyonen beschrijven: deeltjes die sneller dan het licht gaan! Voor deze deeltjes is het kwadraat van de massa negatief, en de massa \( m \) zelf neemt dus een imaginaire waarde aan (wortel van \( -1 \) is een zogeheten complex getal, i). Dit klinkt al wat eigenaardig, maar de eigenschappen van deze tachyonen worden nog bijzonderder wanneer we kijken hoe hun energie van hun snelheid afhangt. Hiervoor is het handig om bovenstaande formule te herschrijven als
\( E^2 = \frac{-m^2}{v^2-1} \),
zodat de teller \( -m^2 \) positief is. Hieruit kunnen we inderdaad zien dat de snelheid groter dan de lichtsnelheid moet zijn, \( v>1 \) (ter herinnering: c=1 is voor ons de lichtsnelheid), om een goed gedefinieerde energie te hebben. Maar we zien ook dat als we de snelheid verhogen de noemer van de breuk groter wordt, en dus de energie kleiner wordt. Oftewel, er komt energie vrij door een tachyon te versnellen! Aangezien natuurkundige systemen meestal hun energie proberen te minimaliseren, betekent dit dat tachyonen alsmaar sneller gaan bewegen.
Cherenkovstraling
Een merkwaardig fenomeen dat nu zou kunnen plaatsvinden is zogenaamde Cherenkovstraling. Deze straling komt voor wanneer een geladen deeltje zich sneller voortbeweegt dan de snelheid van licht in het medium waarin het zich bevindt. Stel bijvoorbeeld dat we een elektron hebben dat met 0,9c (90% van de lichtsnelheid) door het water schiet, terwijl de snelheid van licht daarin iets minder dan 0,8c is. Dan creëert het elektron een golf van Cherenkovstraling achter zich, zoals we bijvoorbeeld waarnemen in de koelbakken van kernreactoren.
Voor tachyonen die elektrisch geladen zijn betekent dit nu dat zij altijd Cherenkovstraling zullen veroorzaken — zij bewegen namelijk zelfs in het vacuum sneller dan licht.

Tot nu toe hebben we nog nooit Cherenkovstraling van tachyonen waargenomen, en ook op andere wijzes hebben we dit soort bijzondere deeltjes nog niet gedetecteerd. Sterker nog, binnen de theoretische natuurkunde wordt de aanwezigheid van tachyonen vaak gezien als een pathologische eigenschap van een model. Ze duiden namelijk op zeer instabiele situaties, waarbij deeltjes oneindig kunnen blijven versnellen en straling veroorzaken zonder dat dit ook maar enige energie kost. Hoewel we het hier dus gehad hebben over deeltjes die juist niet lijken te bestaan, is het zoals je ziet wel heel interessant om in gedachten experimenten met zulke deeltjes te doen: doordat we géén Cherenkovstraling in de lege ruimte waarnemen, weten we dat de mogelijkheid van tachyonen in de natuur vrijwel uitgesloten is – en ook dat iets níét bestaat is een heel interessante observatie!