
Afbeelding 1. Samensmeltende zwarte gaten.Een artist impression van twee zwarte gaten die samensmelten. Afbeelding: NASA.
Zwaartekrachtsgolven
Het is alweer meer dan anderhalf jaar geleden dat zwaartekrachtsgolven voor het eerst direct waargenomen zijn. Deze golven waren afkomstig van twee samensmeltende zwarte gaten. Twee hemellichamen die om elkaar heen draaien creëren constant zwaartekrachtsgolven. Hierdoor verliezen ze energie, waardoor ze dichter bij elkaar komen. Dit gebeurt dus niet alleen voor zwarte gaten, maar bijvoorbeeld ook voor de aarde die om de zon draait. Omdat de aarde en zon niet zo zwaar zijn, is dit effect heel klein, maar voor twee zwarte gaten kan dit effect zo groot zijn dat ze uiteindelijk bij elkaar komen en samensmelten.
De golven die veroorzaakt worden tijdens dit samensmelten zijn zo energetisch dat ze waargenomen kunnen worden, en dat is precies wat gebeurde op 14 september 2015. Het samensmelten van de zwarte gaten dat toen gemeten werd, vond zo’n 1,3 miljard jaar geleden plaats! Het kost nu eenmaal tijd voor de golven om op aarde te arriveren.
Ellipsen
In dit artikel wil ik nader ingaan op de zwaartekrachtsgolven die gecreëerd worden tijdens het om elkaar heen draaien van twee hemellichamen. In veel gevallen zullen die twee hemellichamen namelijk in de praktijk nooit bij elkaar komen – zoals bijvoorbeeld het geval is bij de aarde en de zon. Maar waar hangt deze samensmelttijd nu precies vanaf?
De baan van twee hemellichamen die om elkaar heen draaien, zoals de aarde en de zon, of the maan en de aarde, kunnen we beschrijven met een ellips – zie afbeelding 2. Hierbij staat één van de lichamen in het brandpunt, aangegeven met F2, en het andere beweegt over de ellips. De vorm van een ellips wordt beschreven door twee variabelen: de halve lange as, a, en de excentriciteit, e. Hoe die laatste variabele gedefiniëerd is, is in de afbeelding te zien: de afstand van de brandpunten tot het middelpunt van de ellips is gelijk aan e·a.
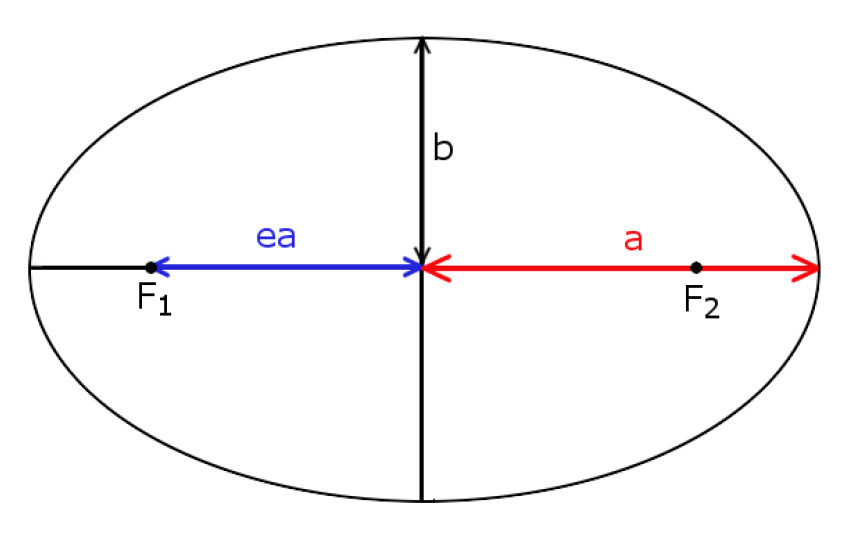
Afbeelding 2. Een ellips.Een ellips met halve lange as a en excentriciteit e. De afstand van het centrum tot de focus is e·a. Als e = 0 is de ellips een cirkel en als e bijna 1 is, is de ellips bijna een lijn. (Deze en onderstaande afbeeldingen zijn afkomstig uit de bachelorscriptie van de auteur.)
De excentriciteit neemt waarden aan tussen 0 en 1. Wanneer de excentriciteit 0 is, is de ellips een cirkel en wanneer e bijna 1 is, is de ellips bijna een lijn. De excentriciteit geeft dus aan hoe plat de baan is: hoe hoger de waarde, hoe platter de ellips. De halve lange as geeft aan hoe groot de ellips is – je kunt die zien als een maat voor de afstand tussen de twee objecten.
Hoe snel smelten hemellichamen samen?
Als er verder geen andere hemellichamen in de buurt zijn die zwaar genoeg zijn, blijven de waarden van a en e constant. De baan van de aarde om de zon verandert bijvoorbeeld minimaal. Het blijkt nu dat een systeem dat “platter” is, meer energie verliest aan zwaartekrachtsgolven, waardoor de twee objecten sneller bij elkaar komen. Hoe dichter de excentriciteit bij 1 ligt, hoe korter de samensmelttijd wordt. Verder spelen ook de massa’s van de twee hemellichamen mee: hoe zwaarder ze zijn, hoe sneller ze samensmelten. Dit is ook de reden dat het samensmelten wel bij zwarte gaten kan gebeuren, maar niet bij de aarde en de zon.
Er bestaan mechanismen die ervoor kunnen zorgen dat hemellichamen die niet zwaar genoeg zijn of een baan met een te kleine excentriciteit hebben, toch wel bij elkaar kunnen komen. Een voorbeeld is het Kozai-mechanisme dat kan optreden als er nog een derde hemellichaam is. Voor het gemak zullen we uitgaan van een systeem van 3 zwarte gaten die om elkaar heen draaien, alweer omdat het effect niet groot genoeg is als één van de objecten niet zwaar genoeg is.
Niet alle systemen van 3 zwarte gaten kunnen voor miljoenen jaren bij elkaar blijven. Vaak is zo’n systeem instabiel en wordt één van de zwarte gaten binnen korte tijd de ruimte in geschoten waardoor er weer maar twee zwarte gaten overblijven. Het blijkt dat het systeem wel stabiel is als het derde zwarte gat relatief ver weg is. Het blijkt ook dat we zo’n systeem op korte tijdschalen (vergeleken met de tijd die het kost om één omloop te maken) kunnen zien als twee systemen die allebei bestaan uit twee hemellichamen. We kunnen het hele systeem dus beschrijven met twee ellipsen. Het eerste systeem bestaat uit de binnenste twee zwarte gaten. Voor het andere systeem zien we de binnenste twee zwarte gaten als 1 object; dit object vormt samen met het derde zwarte gat het buitenste systeem.
De invloed van het derde zwarte gat
Zoals al eerder gezegd zouden de excentriciteit en halve lange as van de baan van de binnenste twee zwarte gaten constant blijven als dit derde zwarte gat er niet was. Op korte tijdschalen, weer vergeleken met de omlooptijd van deze 2 objecten, veranderen deze waarden dan ook niet zichtbaar door de aanwezigheid van het derde zwarte gat. Op grote tijdschalen kunnen de excentriciteit en halve lange as wel veranderen. De mate van platheid van de baan van de binnenste twee zwarte gaten verandert dus en dit heeft invloed op de mate van energieverlies aan zwaartekrachtsgolven.
Het blijkt dat de excentriciteit van het binnenste systeem periodiek gedrag vertoont als er een derde zwarte gat is en dit wordt het Kozai effect genoemd. De sterkte van dit effect hangt natuurlijk weer enorm af van de verschillende variabelen die de beide ellipsen beschrijven. Het blijkt bijvoorbeeld dat dit effect heel sterk is als de beide ellipsen bijna loodrecht op elkaar staan. Als het Kozai-effect krachtig genoeg is, kan het derde zwarte gat er zelfs voor zorgen dat de excentriciteit van de baan van de binnenste twee zwarte gaten heel dicht bij 1 komt. Tijdens de perioden dat de baan heel plat is, wordt er veel meer energie verloren dan als de baan bijna rond is. Hierdoor kan het dus zijn dat een paar zwarte gaten dat zonder dit derde zwarte gat niet zou samensmelten, dat door de invloed van het derde zwarte gat wel doet.
Een voorbeeld doorgerekend
In afbeelding 3 zien we een voorbeeld waarbij het Kozai-effect optreedt. We kijken hier naar een systeem waar de binnenste twee zwarte gaten 10000 keer zo zwaar als de zon zijn, en het derde zwarte gat een miljoen keer zo zwaar als de zon is.
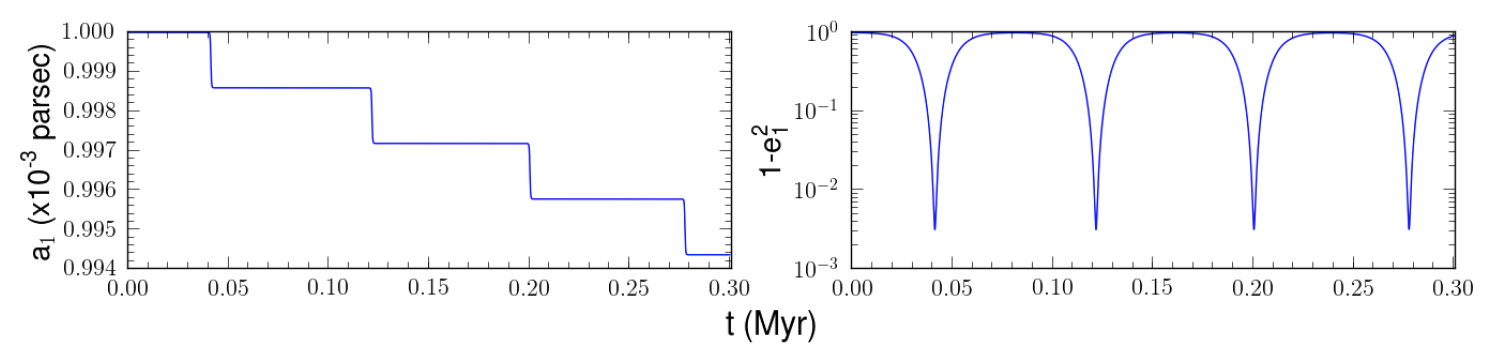
Afbeelding 3. Het Kozai-effect.De waarden van de halve lange as en de excentriciteit van een systeem van twee zwarte gaten onder invloed van een derde zwarte gat. (Voor het rekenwerk dat in deze en onderstaande grafieken is weergegeven is gebruik gemaakt van code uit AMUSE. Details zijn te vinden in de bachelorscriptie van de auteur.)
De excentriciteit begint met een waarde van 0,1 en als het derde zwarte gat er niet zou zijn, zou die waarde ook zo blijven. In de rechtergrafiek in afbeelding 3 zie je dat dat nu niet zo is: door het derde zwarte gat gaat de excentriciteit periodiek gedrag vertonen. In de pieken van de grafiek neemt de excentriciteit waarden aan die heel dicht bij 1 liggen.
In de linkergrafiek in afbeelding 3 zie je de ontwikkeling van de halve lange as. Hier zie je ook de sterke invloed van de excentriciteit op het energieverlies door zwaartekrachtsgolven, en dus op het afnemen van de afstand tussen de twee zwarte gaten. Alleen als de excentriciteit heel dicht bij 1 komt, bij de pieken in de rechtergrafiek, zie je in de linkergrafiek de halve lange as duidelijk afnemen. In afbeelding 3 kun je maar een klein stukje van de ontwikkeling van het systeem zien. In afbeelding 4 zie je de hele ontwikkeling totdat de twee zwarte gaten bijna samensmelten. Hier zijn de oscillaties van de excentriciteit veel minder duidelijk te zien, maar je ziet wel dat na bijna 15 miljoen jaar de twee zwarte gaten samenkomen. Zonder dit derde zwarte gat zou dit pas na zo’n 20.000 keer de leeftijd van het heelal gebeuren – dus 20.000 keer 14 miljard jaar! Hier zie je hoe groot de invloed van het Kozai effect kan zijn.
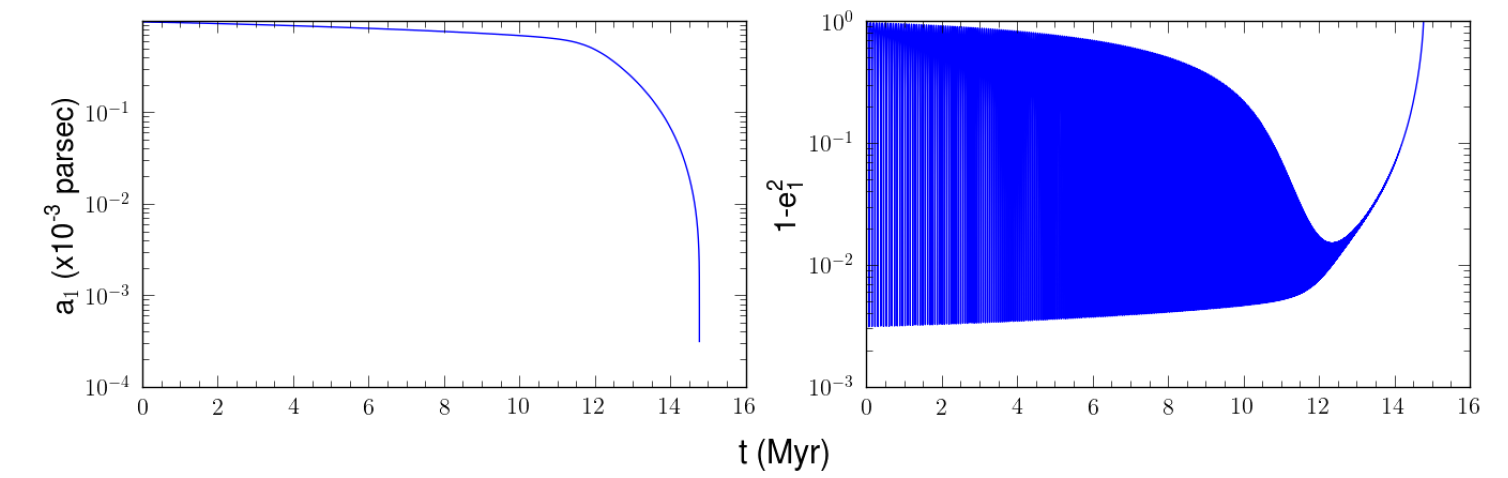
Afbeelding 4. Het Kozai-effect op lange termijn.De hele ontwikkeling van de halve lange as en excentriciteit van ons voorbeeld.
Meer samensmeltingen
Met het Kozai-mechanisme moet je rekening houden als je wilt schatten hoe vaak je een samensmelting van zwarte gaten kunt waarnemen. Als je naïef alleen de paren van zwarte gaten meeneemt in die schatting, krijg je een te laag aantal samensmeltingen. Je moet ook meerekenen hoe vaak er zich een derde zwarte gat in het systeem bevindt, want zoals we gezien hebben kan dat ervoor zorgen dat de binnenste twee zwarte gaten samensmelten terwijl ze dat zonder dit derde gat misschien niet zouden doen! Voor experimentatoren zoals die van LIGO zijn effecten zoals die hierboven zijn beschreven dus cruciaal om goed te bepalen hoe vaak ze een spectaculaire waarneming zoals die van anderhalf jaar geleden kunnen verwachten.