Quantumcomputers (1): Makkelijk of moeilijk?

Afbeelding 1. Computers toen en nu.Links: een quantumcomputer nu, gebouwd door IBM. Rechts: de eerste computer van Nederland in 1952, de ARRA. Bron rechterafbeelding: Centrum Wiskunde & Informatica.

De drie delen van dit dossier zijn als volgt ingedeeld:

Deel 1: Voor quantumcomputers zijn sommige dingen ‘makkelijk’ die voor een normale computer ‘moeilijk’ zijn. Dat stelt ze in staat problemen op te lossen die onmogelijk in een redelijke tijd op een normale computer op te lossen zijn. Bij een ‘redelijke tijd’ kun je denken aan zoiets als de leeftijd van het universum!

Deel 2: Het gemak waarmee quantumcomputers sommige berekeningen kunnen doen stelt ze mogelijk in staat om de code waarmee veel berichten op het internet worden beveiligd te kraken. Om te zien hoe ze dat eigenlijk doen zullen we eerst kijken naar hoe deze code werkt. Dan zullen we uitleggen hoe een gewone computer werkt. Waar een gewone computer met bits rekent, rekent een quantumcomputer met quantummechanische bits: qubits.

Deel 3: Hoe bouwt men nu zo’n quantumcomputer? Quantumcomputers zijn op dit moment nog in het tijdperk dat de jaren ’50 en ’60 voor de gewone computers waren. Er wordt dus door natuurkundigen en computerwetenschappers nog actief onderzoek gedaan naar hoe je een quantumcomputer het beste bouwt, en wat je ermee kunt als ze er eenmaal zijn. Hoe zal een toekomst met quantumcomputers eruitzien?

Makkelijk vs. moeilijk

Makkelijk

Quantum- en gewone computers werken altijd volgens vaste ‘recepten’. Het recept vertelt ze precies welke stappen er gevolgd moeten worden om tot een oplossing van een bepaald probleem te komen. Zo’n computerrecept noemt men een algoritme en een voorbeeld van een probleem is: ‘wat is de uitkomst van getal a plus getal b?’. Het algoritme dat wordt gebruikt om dat probleem op te lossen zullen we hier beschrijven.

Het algoritme om ‘a + b‘ te berekenen is heel makkelijk. Iedereen die de basisschool met succes heeft afgerond kent dit algoritme, ook al is niet iedereen zich daarvan bewust. Als we twee getallen bij elkaar optellen, bijvoorbeeld

40320
3091
——— +,

dan begin je rechts en tel je eerst 0 op bij 1, dat geeft 1. Je schrijft een 1 op. Vervolgens tel je 2 op bij 9, dat geeft 11. Je schrijft een 1 op en hevelt de andere 1 over naar de volgende positie (‘onthouden’). Vervolgens tel je 1 bij 3 en 0 op, enzovoort. Je stopt als er geen getallen meer over zijn, en dan staat het antwoord op papier. Een computer volgt hetzelfde algoritme maar dan een stuk sneller.

Wat dit probleem makkelijk maakt is het volgende: als de getallen één getal langer worden, duurt de berekening precies één stapje langer. Dit leidt tot de definitie van ‘makkelijk’ zoals we hem hier zullen gebruiken. Een makkelijk probleem is een probleem waarvoor het vinden van een oplossing één stapje langer duurt wanneer het probleem één stapje moeilijker wordt.^[1]

Het is belangrijk te beseffen dat we dus niet kijken naar hoe lang een computer over het vinden van de oplossing doet, maar naar hoeveel langer dezelfde computer erover doet als we het probleem één stap moeilijker maken.

Moeilijk

Wat is nu een ‘moeilijk’ probleem? Het volgende probleem is erg^[2] moeilijk. Stel: je woont in Amsterdam en je moet in één dag iets ophalen bij een broer in Breda en een nicht in Culemborg. Je kunt eerst naar Breda en daarna naar Culemborg gaan, maar misschien is het sneller om eerst naar Culemborg te rijden en dan naar Breda. Er zijn twee verschillende routes, maar welke is de kortste?

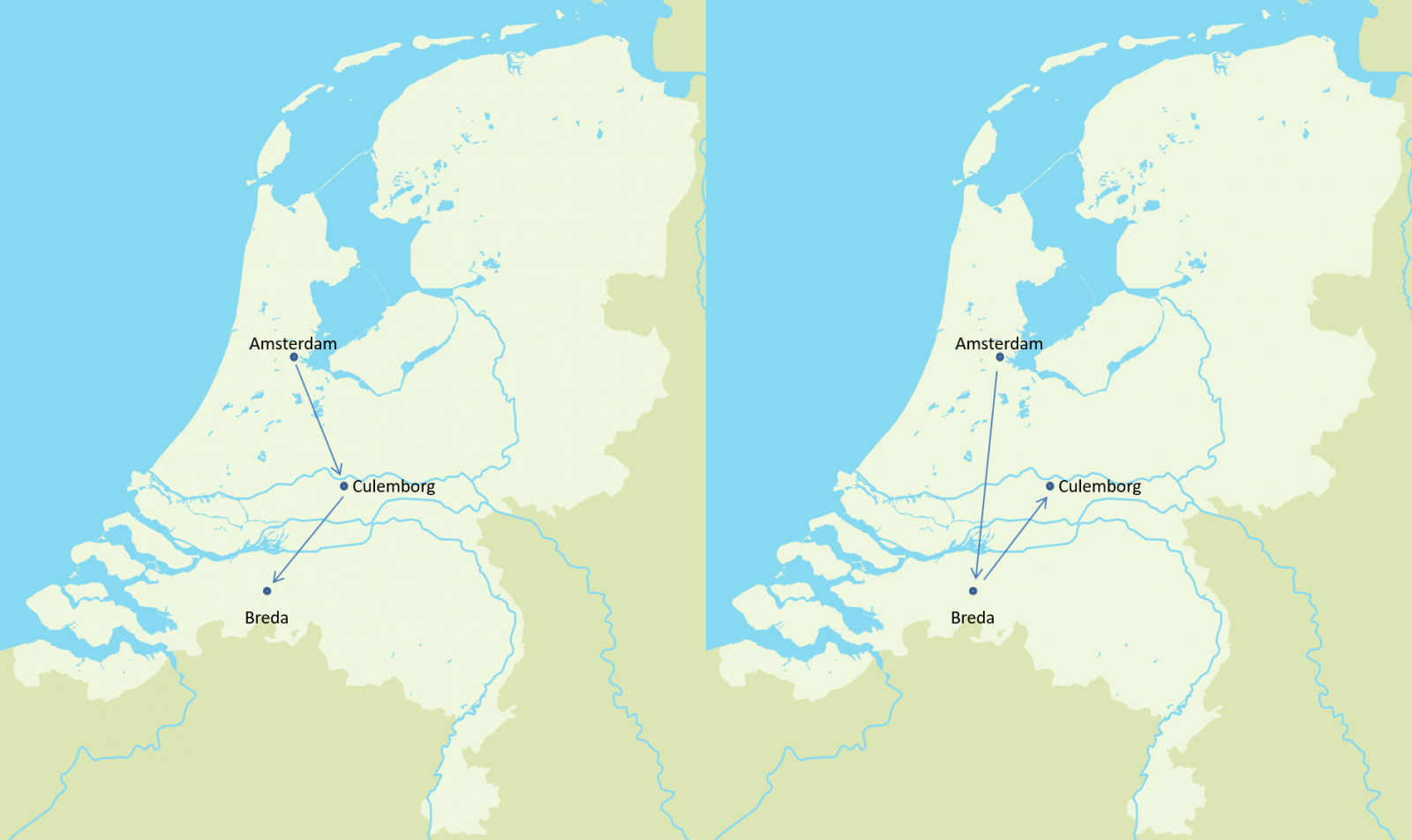
Afbeelding 2. Amsterdam, Breda en Culemborg.De twee mogelijke routes als je vanuit Amsterdam zowel Breda als Culemborg wilt bezoeken.

In dit voorbeeld is de snelste route snel gevonden, maar herinner je dat het er juist om gaat hoeveel moeilijker het vinden van een oplossing wordt als we het probleem één stap ingewikkelder maken. In dit geval doen we dat door een stad toe te voegen.

Stel je daarom eens voor dat je op dezelfde dag ook nog de quantumcomputer wilt bekijken die in Delft staat. Je kunt dan denken: ‘ik bezoek gewoon de steden op alfabetische volgorde’, maar waarschijnlijk is er een tijds- en milieubewustere optie. Misschien kun je beter eerst naar Delft, dan naar Culemborg en dan pas naar Breda gaan; of toch maar eerst naar Culemborg, dan naar Breda en tot slot naar Delft. In totaal zijn er nu al zes verschillende routes.

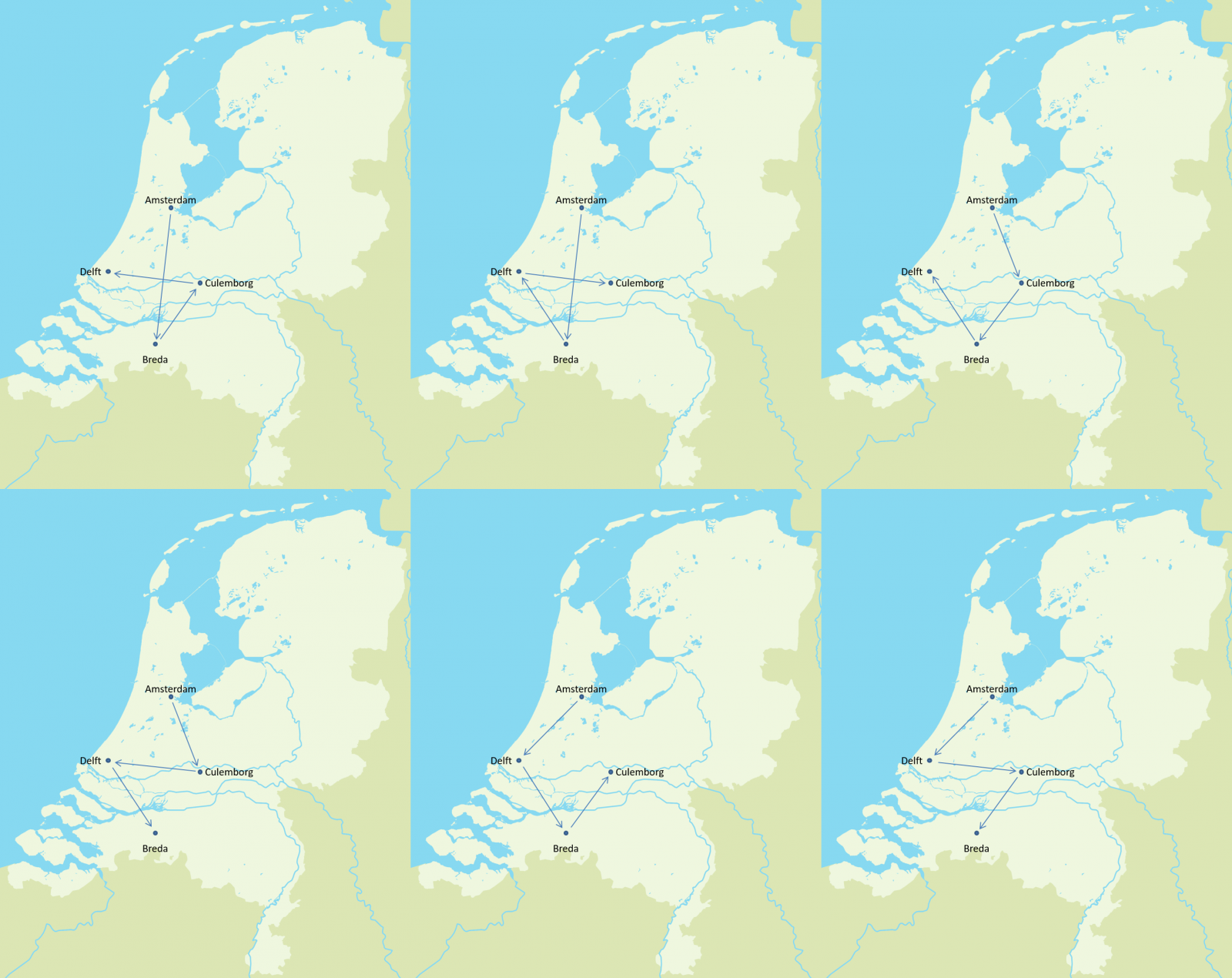
Afbeelding 3. Amsterdam, Breda, Culemborg en Delft.Als je één stad aan het probleem toevoegt, zijn er zes mogelijke routes.

Merk op dat we maar één stad hebben toegevoegd, maar dat er drie keer zoveel mogelijke routes zijn! Voegen we nog een stad toe, dan zijn er nog eens vier keer zoveel mogelijke routes, enzovoort. Dit probleem valt dus beslist niet in de categorie ‘makkelijk’ zoals we die zojuist hebben gedefinieerd.

Wat dit probleem voor een computer zo moeilijk maakt, is dat er geen wezenlijk andere algoritmen zijn om de kortste route uit te rekenen dan domweg alle routes een voor een af te gaan. Als je heel veel steden wilt bezoeken, moet een computer enorm veel rekenstappen maken. Het probleem wordt al snel onmogelijk om op te lossen, ook al zou je een snelle computer hebben en die tijdens de gehele levensduur van de aarde laten rekenen.^[3]

Om een idee te krijgen van hoe snel het uit de hand loopt: als je ook nog naar het planetarium in Franeker wilt, en naar familie in Groningen, Hengelo en IJsselmuiden, dan zijn er al 40.320 verschillende routes!^[4]

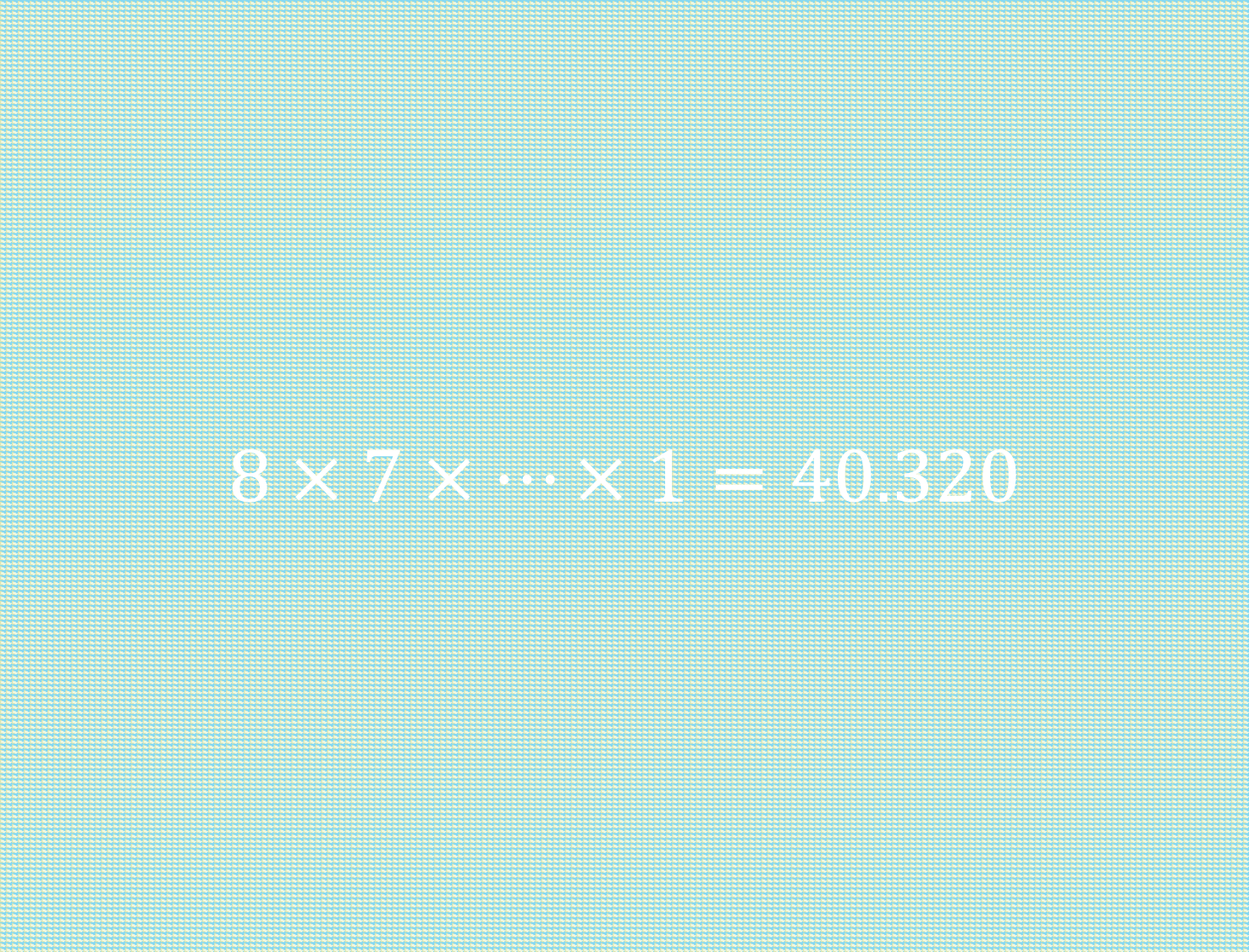
Afbeelding 4. Negen steden.Als je in totaal negen steden wilt bezoeken zijn er al 40.320 mogelijke routes. (Op de achtergrond staan echt 40.230 Nederlandjes!)

Dit probleem staat bekend als het handelsreizigersprobleem, en zoals de naam doet vermoeden is het ook interessant voor transportbedrijven. Het probleem heeft ook allerlei andere toepassingen: denk aan de kortste route van een soldeerkop over een chip of een robot die zo snel mogelijk een verzameling producten moet ophalen in een distributiecentrum.

We hebben nu een voorbeeld van een moeilijk probleem gezien, maar wat is nu de algemene definitie? Zoals we die hier zullen gebruiken luidt die: Een moeilijk probleem is een probleem waarvoor het vinden van een oplossing ten minste twee keer zo lang duurt wanneer het probleem één stapje moeilijker wordt.^[5]

Hiërarchie

Het blijkt dat sommige problemen die voor een normale computer in de categorie ‘moeilijk’ vallen, voor een quantumcomputer in de categorie ‘makkelijk’ vallen. Dat betekent dat er naast ‘moeilijk’ en ‘makkelijk’ eigenlijk nog een tussencategorie is: ‘moeilijk voor een normale computer maar makkelijk voor een quantumcomputer’. We zullen zulke problemen voortaan quantum-makkelijk noemen.^[6]

Het bestaan van de categorie ‘quantum-makkelijk’ betekent nadrukkelijk niet dat alle problemen makkelijk zijn voor een quantumcomputer, zoals weleens wordt beweerd! Welke problemen voor gewone- of quantumcomputers precies moeilijk of makkelijk zijn, is nog lang niet precies bekend. Eén van de taken van onderzoekers is om precies dat uit te zoeken – iets wat bijvoorbeeld gebeurt bij het instituut QuSoft in Amsterdam.

Wat we wel vrij zeker weten is dat de voorbeelden van optellen en het handelsreizigersprobleem uitersten zijn: optellen is zelfs voor een gewone computer eenvoudig, en het handelsreizigersprobleem is zo moeilijk dat het zelfs voor quantumcomputers moeilijk is. Een voorbeeld van een probleem daartussenin, dus van de categorie ‘moeilijk voor een normale computer maar makkelijk voor een quantumcomputer’, is de zogenaamde factorisatie. Wat factorisatie is en hoe quantumcomputers daarmee geheime codes kunnen kraken, lees je in deel 2 van dit dossier.

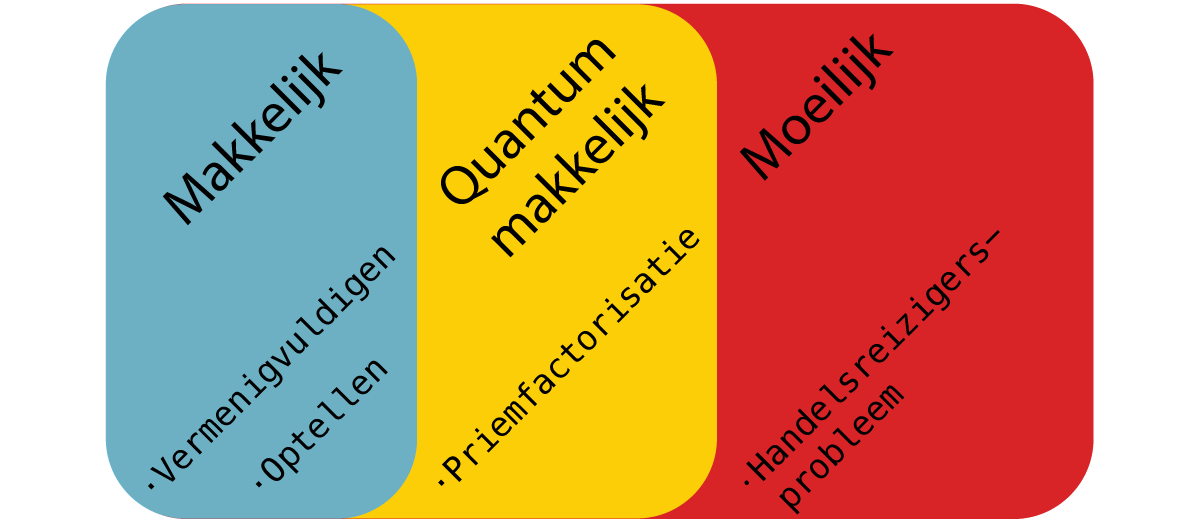
Afbeelding 5. Makkelijk of moeilijk? Er zijn problemen die voor gewone computers moeilijk zijn, maar voor quantumcomputers makkelijk. Zulke problemen noemen we hier ‘quantum-makkelijk’.

Deel 2 van dit dossier verschijnt op vrijdag 24 maart.

^[1] De definitie van de klasse van problemen die men meestal als makkelijk beschouwt is iets ruimer en heet ‘P’. Kort gezegd staat dat voor alle problemen waarvan de rekentijd maximaal een polynomiale functie is van de lengte van de input. Zie hier voor meer informatie.

^[2] Voor de kenners: dit probleem is zelfs ‘NP-moeilijk‘.

^[3] Voor wie wil weten hoe je het aantal mogelijke routes uitrekent langs n steden, met een vast startpunt: bedenk dat je voor de eerste stad die je aandoet kan kiezen uit n − 1 steden. Voor de tweede stad kun je nog kiezen uit n − 2 steden; in twee steden ben je immers al geweest. Als je zo doorgaat tot je alle steden gehad hebt, heb je in totaal (n−1) × (n−2) × … × 1 mogelijke routes gehad. Dit wordt ook wel met een uitroepteken genoteerd als (n−1)!. (Spreek uit: ”n min één – faculteit”).

^[4] Het is een leuke opgave om zelf eens door te rekenen hoe extreem deze groei is. Stel dat je een computer hebt met een kloksnelheid van 10 GHz, en neem aan dat deze per kloktijd precies één route kan nagaan. Met andere woorden: je kunt 10¹⁰ routes per seconde nagaan. Hoe lang doe je er dan over om alle routes tussen 28 steden na te gaan? Hoe verhoudt deze tijd zich tot de verwachte levensduur van de aarde – ongeveer 10 miljard jaar?

^[5] De definitie van de categorie van problemen die men meestal als moeilijk beschouwt is iets ruimer en omvat alle problemen die niet ‘makkelijk’ zijn. Dat wil zeggen: een probleem is moeilijk als er geen algoritme bestaat waarvan de rekentijd maximaal een polynomiale functie is van de inputlengte.

^[6] De officiële terminologie is dat deze problemen vallen binnen de BQP-complexiteitsklasse.