De oneindige reeks
Van oorsprong zijn getallenreeksen het domein van de wiskunde (en in het bijzonder getaltheorie), maar ook in de natuurkunde komen getallenreeksen op meerdere plaatsen terug. In de wiskunde is er trouwens een belangrijk terminologieverschil met de alledaagse taal: een rij is daar een oneindige opeenvolging van getallen zoals (1, 2, 4, 8, 16, …); een reeks is een oneindige optelling van getallen, zoals 1+1/2+1/4+1/8+… . In het dagelijks taalgebruik worden beide echter als ‘reeks’ aangeduid, en dat zullen we hier ook doen. Een belangrijk voorbeeld van een reeks als optelling is de som van alle natuurlijke (oftewel positieve, gehele) getallen, die bijvoorbeeld voorkomt in de snaartheorie en quantumveldentheorie:
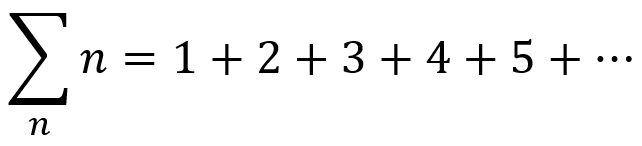
Als we deze getallen optellen tot n = ∞ dan is het duidelijk dat we uiteindelijk een oneindig groot getal krijgen. Toch wordt in de natuurkunde vaak een andere waarde gebruikt voor de uitkomst van deze reeks:
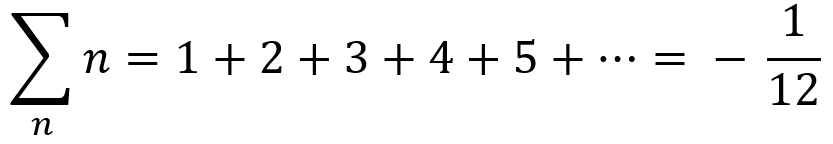
Dit verrassende resultaat kan op verschillende manieren verkregen worden. Één van de bekendste methodes heet Riemann zeta-functie regularisatie. De in eerste instantie puur wiskundige ‘Riemann zeta-functie’ komt wel degelijk in de natuurkunde voor, en wordt bijvoorbeeld gebruikt in de statistische fysica bij het bestuderen van het Riemanngas: een “gas” waarvan de verdeling in de ruimte bepaald wordt door priemgetallen – weer een andere bekende reeks (of wiskundig dus eigenlijk: een rij). Hoe dat precies in z’n werk gaat en waarom we deze functie kunnen gebruiken om de oneindige reeks te berekenen, voert voor nu te ver – vandaag richten we ons op de priemgetallen zelf. Zie voor meer over het optellen van all gehele getallen dit eerdere artikel op onze site.
‘Spelen’ met priemgetallen
Priemgetallen zijn gehele getallen groter dan 1 die alleen door zichzelf en door het getal 1 gedeeld kunnen worden: 2, 3, 5, 7, 11, 13, 17, 19, 23, … Ook priemgetallen worden vanuit de natuurkunde bestudeerd; eerder schreven we bijvoorbeeld al over een methode om priemgetallen te testen met quantummechanica. Maar soms zijn getallenreeksen zélf gewoon heel mooi om mee te ‘spelen’. Zo blijken de priemgetallen een bijzonder patroon te vertonen als we ze plotten met behulp van poolcoördinaten. Dat gaat als volgt in z’n werk. Laten we beginnen met alle gehele getallen, dus 1, 2, 3, 4, 5, … enzovoort. We willen nu aan elk getal twee coördinaten verbinden die een punt in een tweedimensionaal vlak weergeven. Een manier om dit te doen is om voor elk getal het punt te kiezen waarvan de afstand tot de oorsprong (de straal) gelijk is aan het getal, en tegelijkertijd ook de hoek in radialen (ten opzichte van bijvoorbeeld de x-as) gelijk te kiezen aan dat getal. Het getal n wordt dan het volgende punt in het (x,y)-vlak:
![]()
Als we dat voor de getallen 1 t/m 10 doen krijgen we het volgende plaatje:
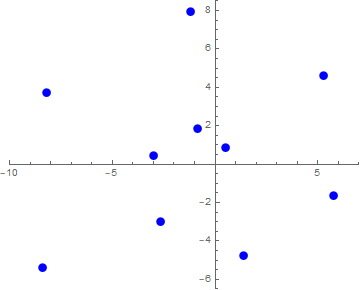
Afbeelding 1. Getallen in poolcoördinaten.De eerste tien gehele getallen geplot met poolcoördinaten.
Als je goed kijkt zie je het patroon misschien al: er ontstaat een spiraal! Dit is duidelijker te zien als we de punten verbinden:
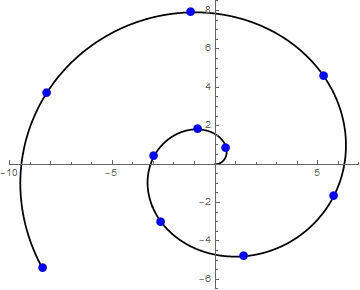
Afbeelding 2. Een spiraalpatroon.Dezelfde punten als in afbeelding 1, ditmaal verbonden met een lijn.
Je zou je nu kunnen afvragen wat er gebeurt als we alleen de priemgetallen plotten. Het blijkt dat we dan ook prachtige patronen krijgen, die ons veel vertellen over die priemgetallen. Om die patronen te kunnen zien, moeten we heel veel priemgetallen plotten en langzaam uitzoomen tot we steeds meer priemgetallen in kaart hebben gebracht. Rondom de oorsprong zien we dan ‘spiraalarmen’ ontstaan (links in afbeelding 3), en als we nog verder uitzoomen zien we bovendien rechte lijnen (rechts in afbeelding 3).

Afbeelding 3. Een patroon in de priemgetallen.Elk stipje is een priemgetal geplot in poolcoördinaten. Links nog relatief dicht bij de oorsprong (relatief kleine priemgetallen); rechts verder uitgezoomd. Bron: 3Blue1Brown.
Deze prachtige visualisatie is te vinden in een filmpje van het YouTube-kanaal 3Blue1Brown. In het (Engelstalige) filmpje wordt ook uitgelegd waarom deze patronen ontstaan – dat volgt uit de wiskundige eigenschappen van priemgetallen. Dit bewijst maar weer eens dat iets op het eerste gezicht onzinnigs (want waarom zou je priemgetallen op deze manier plotten?) wonderschone gevolgen kan hebben – én ons nog iets kan leren over wiskunde.
Nog een tip van de redactie: dit jaar heeft de AIVD voor het eerst ook een junioreditie van de kerstpuzzel uitgebracht – uiteraard ook geschikt voor oudere puzzelaars, maar antwoorden inzenden mag t/m 15 jaar.