
In een eerder artikel zagen we al eens hoe botsende blokken op verrassende wijze de decimalen van pi kunnen reproduceren. Daarvoor was niet meer nodig dan in een slim gekozen opstelling simpelweg het aantal botsingen tellen. Er blijkt echter nog veel meer aan de hand in dit bijzondere gedachte-experiment: recent realiseerde de Amerikaanse wetenschapper Adam Brown zich dat dit verschijnsel in de klassieke mechanica identiek is aan een zoekalgoritme voor quantumcomputers! Hiermee geven de botsende blokken een verhelderende blik op een nogal complex quantumalgoritme. In dit artikel bespreek ik deze opmerkelijke connectie tussen klassieke mechanica en quantummechanica.
Klassieke mechanica: botsende blokken en pi
Laat ik beginnen door eerst kort het verhaal van de botsende blokken samen te vatten. We nemen een muur met daarnaast twee blokken, waarvan het verste blok het grootste is. Dit verste blok schuiven we vervolgens met volle vaart in de richting van het andere blok en de muur. Eerst zal het grote blok tegen het kleine blok botsen, daarna kaatst het kleine blok tegen de muur, waarna het weer tegen het grote blok zal botsen. Dit proces blijft zich herhalen totdat het grote blok zo snel van de muur weg beweegt dat het niet meer ingehaald kan worden door het kleine blok, oftewel: tot het grote blok ontsnapt aan het kleine blok. Ter verduidelijking is dit proces stapsgewijs weergegeven in afbeelding 1.
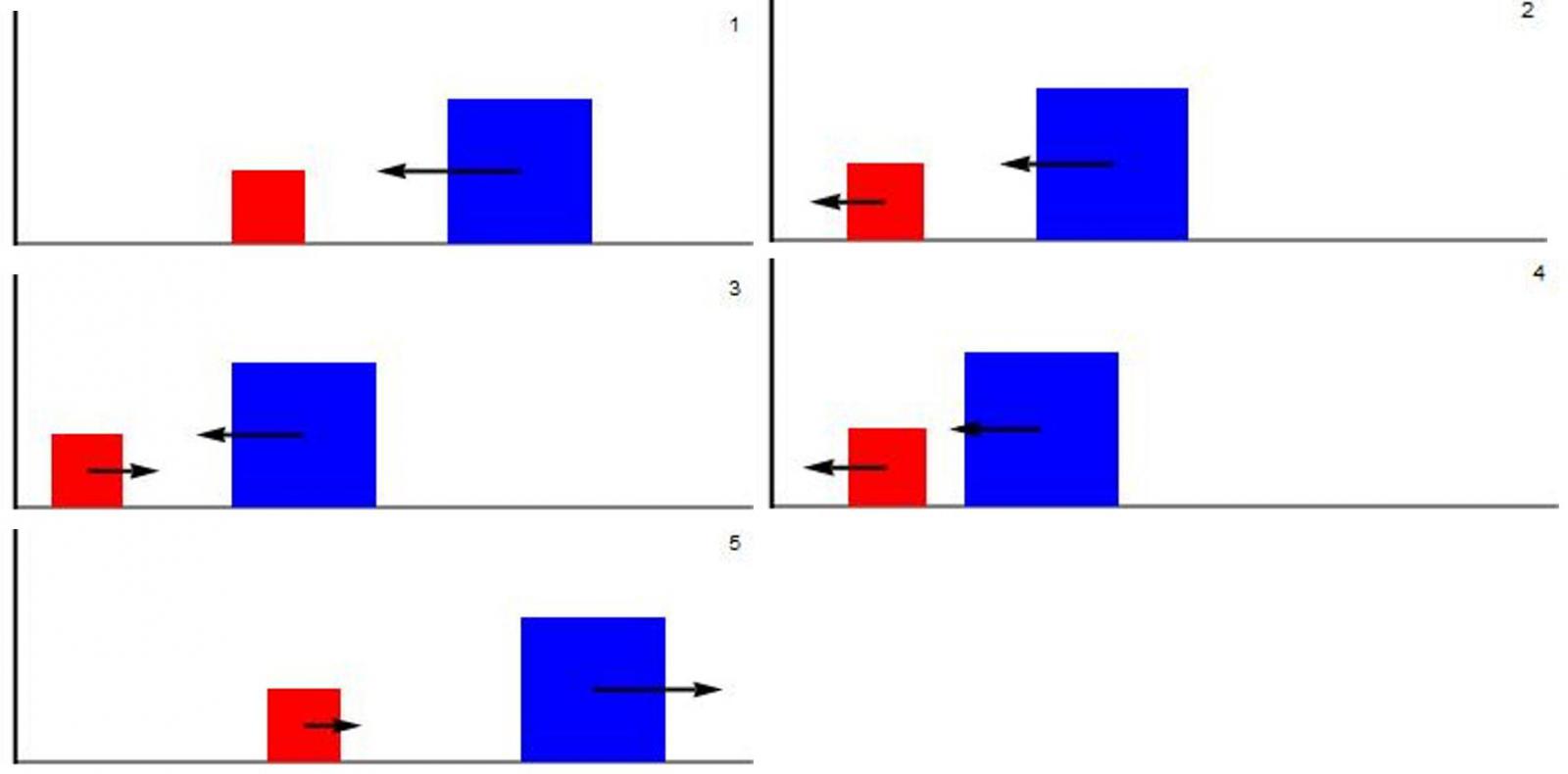
Afbeelding 1. Botsende blokken.Het blauwe, zware blok botst diverse malen met het rode, lichte blok, dat op zijn beurt steeds tegen de muur botst en omkeert.
Tel nu het aantal botsingen dat de blokken hebben gemaakt en je zult in dat getal, onder de juiste voorwaarden, de decimalen van π herkennen. Als we bijvoorbeeld een groot blok nemen dat honderd keer zo zwaar is als het kleine blokje, dan tellen we 31 botsingen. Is het grote blok tienduizend maal zo zwaar, dan tellen we 314 botsingen. Hoe kwamen we ook alweer tot dit verrassende resultaat? Met behulp van de behoudswetten van energie en impuls beredeneerden we dat we de configuratie van dit proces konden afbeelden op een cirkel. Dit is in afbeelding 2 weergegeven, waarbij op de x-as de snelheid van het grote blok staat, en op de y-as de snelheid van het kleine blokje. Vervolgens konden we meetkundige trucjes met omtrekshoeken en middelpuntshoeken toepassen om het aantal botsingen aan de decimalen van π te relateren. We vonden namelijk dat, voor een groot blok dat 102d maal zo zwaar is als het kleine blok, er ongeveer 10dπ botsingen plaatsvinden. Oftewel: het aantal botsingen wordt dan inderdaad gegeven door de eerste d decimalen van π.
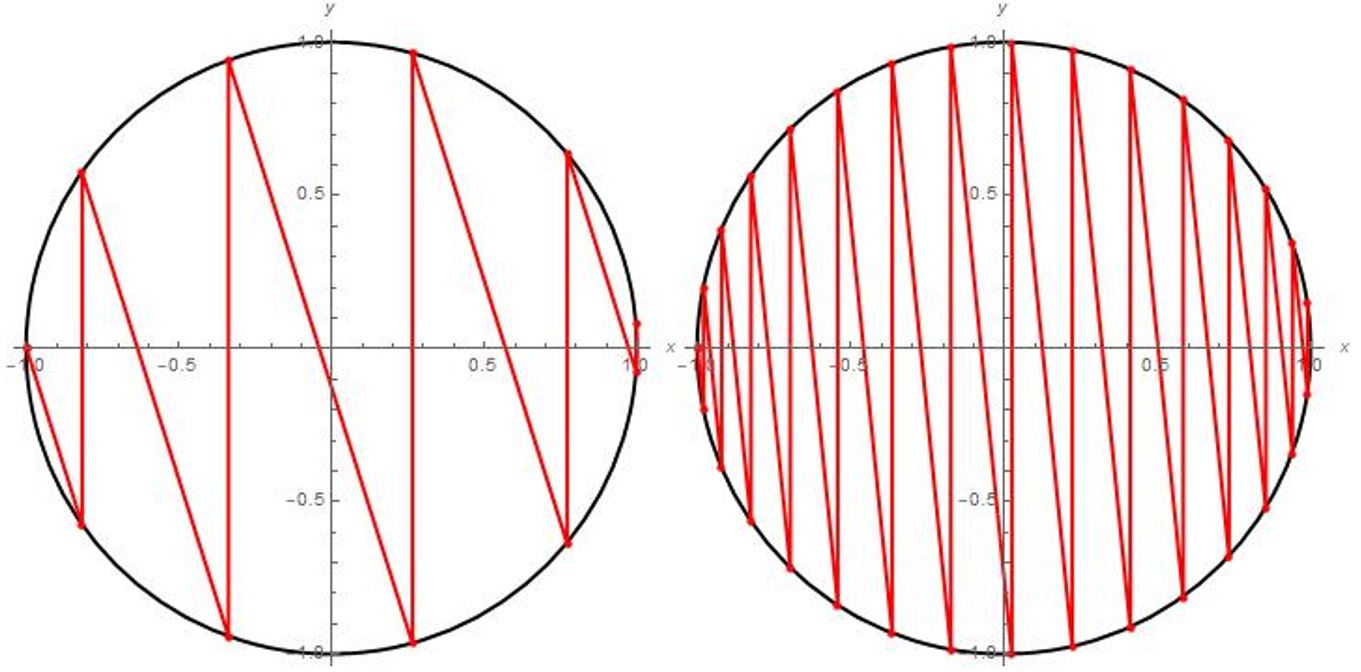
Afbeelding 2. Het botsinsproces grafisch weergegeven.Twee voorbeelden van het hele botsingsproces met verschillende waarden van de massa’s van de blokken.De rode lijn geeft aan hoe de snelheden van de twee blokken (uitgezet langs de twee assen) steeds veranderen. Dat alle eindpunten op een cirkel liggen is een gevolg van energiebehoud.
Quantummechanica: Grovers algoritme
Dit brengt ons bij de andere kant van het verhaal, het quantumalgoritme. Stel je voor dat je een lange ongesorteerde lijst hebt van een miljoen namen, en erachter wilt komen waar jouw naam in die lijst staat. De enige manier waarop je daar zelf achter kunt komen, is door één voor één iedere naam uit de lijst te bekijken. Gemiddeld genomen zal jij (of je computer) dan een half miljoen namen moeten bekijken voordat je jouw eigen naam bent tegengekomen. De computerwetenschapper Lov Grover bedacht in 1996 een algoritme voor quantumcomputers dat deze opdracht veel sneller kan uitvoeren. Voor een lijst van N namen geeft zijn algoritme namelijk binnen π √N / 4 stappen de plaats waar jouw naam staat. Dit betekent dat Grovers algoritme minder dan duizend stappen nodig heeft om jouw naam uit deze lijst van een miljoen namen te vissen! En hoe langer die lijst wordt, hoe efficiënter Grovers algoritme relatief gezien is. Dit is een van de voorbeelden van een opdracht die een quantumcomputer veel sneller zou kunnen uitvoeren dan een gewone computer. Goed om te weten, maar het bouwen van een quantumcomputer blijkt toch erg lastig. Recent zijn wetenschappers van Google er namelijk pas voor het eerst in geslaagd om een prototype quantumcomputer te bouwen die een berekening sneller kan uitvoeren dan een (normale) supercomputer! Er is voor computerwetenschappers dus nog het nodige werk aan de winkel.
Maar hoe werkt dit quantum-zoekalgoritme nu precies? Voordat ik die vraag kan beantwoorden, moet ik uitleggen hoe data op een quantumcomputer zouden worden opgeslagen. Op een normale computer kunnen we de namenlijst bit voor bit uitlezen, maar voor quantumcomputers werkt dit iets anders. Daar associëren we namelijk met iedere naam een bepaald getal. Deze getallen samen specificeren de quantumtoestand van een bepaald quantummechanisch systeem, wat in dit geval in onze quantumcomputer zit. Als we vervolgens een meting op deze quantumtoestand uitvoeren, krijgen we de positie van één enkele naam daaruit, en de kans op deze naam volgt uit het eraan verbonden getal. Dat klinkt misschien wat abstract, dus laten we daarom naar een voorbeeld kijken:
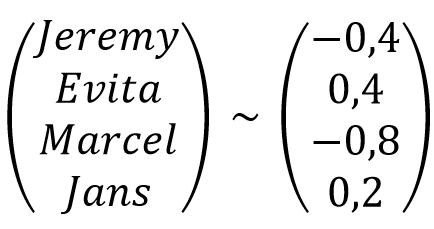
Hier hebben we een lijst van vier namen, en we associëren met iedere naam een bepaald getal. De kans dat de output een specifieke naam is, is echter niet dat getal zelf, maar het kwadraat van dat getal. De kans dat we bij een meting van de toestand bijvoorbeeld de positie van de naam ‘Marcel’ (dus: 3) tegenkomen is
Kans(‘3’) = (-0,8)2 = 0,64.
Ook zullen we bij een meting altijd een naam vinden, aangezien de som van alle kansen uitkomt op
(-0,4)2 + (0,4)2 + (-0,8)2 + (0,2)2 = 1.
Lov Grover stelde zich nu het volgende probleem voor. Stel dat we een ‘black box’ hebben die, voor een (voor ons onbekende) naam, het getal in de bovenstaande lijst met vermenigvuldigt. De vraag is vervolgens hoe we kunnen achterhalen voor welke positie in de lijst de black box dit doet. Laten we zeggen dat de black box deze operatie voor de naam Jans uitvoert. Dan werkt de black box dus op de volgende manier op de getallenlijst
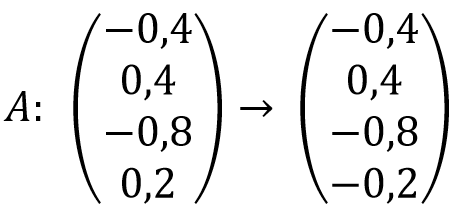
Laten we dit handeling A noemen. Nu is het idee om de toestand zodanig te manipuleren dat een meting van de quantumtoestand met grote zekerheid de positie van de naam ‘Jans’ geeft. Oftewel: we willen de getallenlijst zodanig manipuleren dat de kans op de output ‘4’ ongeveer één is, terwijl die voor de andere uitkomsten vrijwel nul is. Door alleen de black box toe te passen zullen we echter niet in die toestand komen, aangezien dat ons weer in de begintoestand zal brengen:
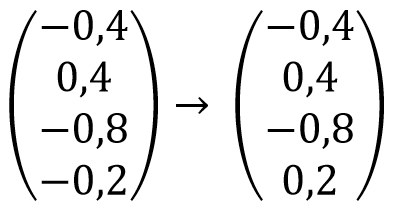
Dit betekent dat we nog een ander soort manipulatie op deze getallenlijst moeten toepassen. Om intuïtie te krijgen voor het soort manipulaties dat we op deze lijst kunnen uitvoeren, is het handig om over deze lijst na te denken als een vector die in een bepaalde richting wijst in een N-dimensionale ruimte. Voor het geval hierboven, met N=4, is dit niet zo makkelijk voor te stellen, dus laten we voor het gemak alleen naar de onderste twee componenten van onze vector kijken:
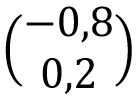
Dan kunnen we deze vector weergeven zoals in afbeelding 3. Hierbij is het interessant om op te merken dat handeling A niets meer blijkt dan het spiegelen van de vector ten opzichte van de horizontale as.
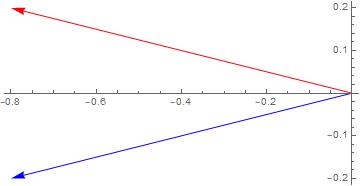
Afbeelding 3. Een spiegeling.Als we een van de componenten van onze vector een minteken, leidt dat tot een spiegeling in een van de assen.
Grover kwam nu met de oplossing door ook nog een andere spiegeling op de vector uit te voeren. Voor deze spiegeling hoeven we alleen te weten hoe de toestand eruit zag voordat we de black box (handeling A) toepasten. De specifieke uitdrukking voor deze spiegeling is echter niet heel verhelderend; die laten we daarom achterwege. Wie toch graag alle technische details wil weten kan die bijvoorbeeld vinden op deze Wikipedia-pagina. Laten we deze tweede actie nu handeling B noemen. Het idee van Grover was dat hij om en om handelingen A en B kon uitvoeren. Hij berekende dat dit ons bij heel goede benadering in de volgende toestand zou brengen:
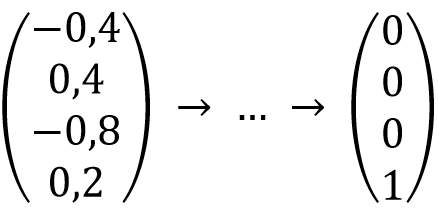
Dan kunnen we simpelweg een meting van deze eindtoestand uitvoeren, wat met vrijwel 100% zekerheid als output de optie ‘4’, dus de positie van ‘Jans’ zal geven. Grovers algoritme is echter, zoals vele quantumalgoritmes, niet perfect, wat betekent dat we niet met volledige zekerheid de positie van de naam Jans krijgen, maar dat er ook nog een kleine kans is op één van de andere posities. Voor de zekerheid zullen we dus nog moeten controleren of de positie die Grovers algoritme aangeeft daadwerkelijk overeenkomt met de naam die we zochten. Zelfs met deze extra test is dit quantumalgoritme echter nog steeds stukken sneller dan een algoritme op een normale computer. En als het algoritme er de eerste keer naast zit, kunnen we het natuurlijk altijd nog paar keer proberen, waarmee de kans dat de quantumcomputer er dan nog steeds naast zit heel erg klein wordt.
Link tussen botsende blokken en Grovers algoritme
Wat nu blijkt is dat de botsende blokken die de decimalen van π produceren, ook een visualisatie geven van Grovers algoritme. Het idee is om ons dit proces voor te stellen als N blokjes van gelijke massa, waarvan N-1 blokjes zijn samengelijmd om het zware blok te vormen, en het overgebleven blokje tussen de muur en het zware blok heen kaatst. Ieder blokje heeft een bepaalde snelheid, en we kunnen deze informatie samenbundelen in een vector met N componenten, waarbij iedere component overeenkomt met één van deze snelheden. Vervolgens kan men stap voor stap bestuderen wat er gebeurt met deze vector na elke botsing. Wat Adam Brown zich realiseerde, is dat deze vector van snelheden precies zo verandert als de vector uit Grovers algoritme. Hij vond namelijk uit dat toepassing van de black box op de toestand (handeling A) overeenkomt met het botsen van het kleine blokje tegen de muur, terwijl de andere spiegeling (handeling B) juist overeenkomt met wanneer het kleine blokje tegen het grote blokje botst. Op een soortgelijke manier wist hij te beredeneren dat bijvoorbeeld behoud van energie voor de botsende blokken overeenkomt met behoud van kans voor de quantumtoestand.
Deze link tussen klassieke mechanica en quantummechanica demonstreert de veelzijdigheid van het toepassen van wiskunde in de natuurkunde. In dit voorbeeld kunnen vectoren zowel worden gebruikt om op de allerkleinste schaal de toestand van een quantummechanisch systeem te specificeren, als om op macroscopische schaal de snelheden van botsende blokken te beschrijven. Op het eerste gezicht lijkt dit soort abstracte wiskunde misschien afschrikwekkend, maar de algemeenheid ervan maakt de toepassing ervan enorm krachtig!