
Afbeelding 1. Richard Feynman (1918-1988).Feynman, de bedenker van de padintegraal, zou op 11 mei 99 jaar zijn geworden.
Groot maal klein
In de wetenschap tellen we vaak een heel groot aantal heel kleine getallen bij elkaar op. Neem een eenvoudig voorbeeld uit de kansrekening: wat is de gemiddelde uitkomst van een worp met een zeszijdige dobbelsteen? Op den duur zullen we elke uitkomst van 1 t/m 6 even vaak kunnen verwachten, en dus is die gemiddelde uitkomst
(1+2+3+4+5+6)/6 = 3,5
Werken we de haakjes in die vergelijking uit, dan kunnen we dat natuurlijk ook schrijven als:
1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 3,5
Aan de linkerkant van deze vergelijking hebben alle termen een duidelijke betekenis: we vermenigvuldigen steeds de waarde van een bepaalde uitkomst (1 t/m 6) met de kans op die uitkomst (1/6), en tellen al die resultaten op.
Zou een slimme ingenieur voor ons een duizendzijdige dobbelsteen weten te ontwerpen, dan zouden we precies dezelfde berekening kunnen doen: de gemiddelde uitkomst zou dan gelijk zijn aan
1/1000 + 2/1000 + 3/1000 + …
Kun je zelf het antwoord van deze lange optelsom vinden? Een handige truc om de uitkomst te berekenen staat onderaan dit artikel. Waar het ons nu echter om gaat is het type van deze berekening: we willen een heel groot aantal heel kleine getallen optellen. Dat is iets wat in de natuurkunde heel vaak voorkomt. Stel bijvoorbeeld dat we de afgelegde weg willen uitrekenen die een onregelmatig versnellende auto in een minuut aflegt. Eén manier om dat te doen is door die minuut in heel veel kleine stukjes op te delen – zo klein dat over die korte tijdsintervallen de snelheid vrijwel constant is. Alle bijbehorende kleine stukjes afgelegde weg zijn dan dus makkelijk uit te rekenen – afstand is immers snelheid maal tijd – en de uitdaging is om al die kleine stukjes vervolgens op te tellen.
Integreren
De bovenstaande procedure is in zekere zin maar een benadering van het echte antwoord. Als we ons experiment met de auto bijvoorbeeld opdelen in intervallen van 1/100e seconde, dan zal de snelheid van de auto in zo’n tijdsintervalletje wel steeds vrijwel constant zijn, maar nooit helemaal. We maken dus een kleine fout als we de resulterende 6000 uitkomsten (één voor elke honderdste seconde in de minuut) bij elkaar optellen. Die fout kunnen we eenvoudig kleiner maken: we kunnen de tijd opdelen in duizendste seconden en dan 60.000 antwoorden optellen, enzovoort. Pas in de limiet waarin we het tijdsintervalletje ‘oneindig klein’ maken, dus vrijwel nul, zullen we exact het juiste antwoord vinden. We tellen dan dus in zekere zin oneindig veel oneindig kleine getallen op!
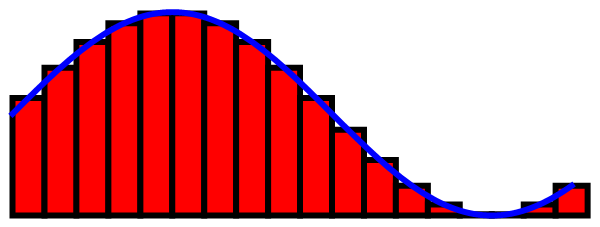
Afbeelding 2. Integreren.Om te integreren benaderen we een steeds veranderende functie door aan te nemen dat die functie op kleine intervallen constant blijft. Hoe kleiner we die intervallen maken, hoe beter die benadering wordt. Hier is de oppervlakte onder de blauwe, vloeiende lijn bijvoorbeeld bij zeer goede benadering gelijk aan de oppervlakte van de rode balkjes. Merk op dat we hier, net als in de voorbeelden, een groot aantal kleine oppervlakjes moeten optellen. Hoe groter dat aantal en hoe kleiner de oppervlakjes, hoe beter de benadering.
Dit ‘oneindig groot maal oneindig klein’ klinkt misschien niet als iets wat wiskundig heel goed gedefinieerd is, maar het mooie is dat het wel mogelijk is om de bovenstaande procedure exact te maken. Dat dat kan, werd al in de 17e eeuw ontdekt door de bekende wetenschapper Isaac Newton en zijn tijdgenoot Gottfried Leibniz. Over de ruzie die die twee vervolgens kregen over wie nu de echte bedenker van dit idee was, schreven we al eerder een artikel. De methode die Leibniz en Newton ontdekten is niets anders dan wat VWO-leerlingen vandaag de dag bij Wiskunde B leren als integreren.
Oneindig, oneindiger, oneindigst
Vooral in de quantummechanica komt de techniek van het integreren vaak van pas. Quantummechanica is immers “kansrekening voor gevorderden”: in een quantum-experiment is er niet sprake van één mogelijke uitkomst, maar van een heel scala aan mogelijke uitkomsten, elk met een bijbehorende kans. Net zoals we de weg van de auto hierboven in kleine stukjes konden opdelen, zo kunnen we ook de “ruimte” van mogelijke quantumuitkomsten van een experiment in kleine stukjes opdelen. Vermenigvuldigen we die uitkomsten met de bijbehorende kansen, tellen we de resultaten op, en nemen we net als bij de auto de limiet voor oneindig kleine “uitkomst-intervallen”, dan weten we de verwachte uitkomst van het quantum-experiment.
Wat Richard Feynman in de jaren ’40 al inzag, was dat het in quantumtheorieën zelfs nog een stap ingewikkelder kan. Als we in een quantumexperiment bijvoorbeeld de plaats van een deeltje binnen een bepaald meetapparaat meten, kan die uitkomst oneindig veel waarden hebben – van “helemaal links in het apparaat” tot “helemaal rechts in het apparaat”, en overal daar tussenin. Die situatie is dus niet veel anders dan die van de auto op de weg, en de “klassieke” wiskunde van het integreren is daar dus van toepassing.
Maar wat als ons quantummechanische experiment gaat over de toestand van een veld zoals het elektromagnetische veld? Een dergelijk veld heeft op elke plaats in de ruimte een bepaalde waarde, en wordt dus weergegeven door oneindig veel getallen die elk oneindig veel verschillende waarden kunnen aannemen. De “ruimte” van alle mogelijke situaties is dus overweldigend groot! Kunnen we zelfs in zo’n geval nog alle verschillende mogelijke uitkomsten optellen? Het antwoord is zowel “ja” als “nee”.

Afbeelding 3. Velden.Elektrische en magnetische velden hebben op elk punt in de ruimte een waarde. Dit kan mooi weergegeven worden door een magneet in wat ijzervijlsel te leggen: we zien dan dat het magnetische veld op elk punt een grootte en een richting heeft. Afbeelding: Newton Henry Black.
Padintegralen
Het “ja”-deel van het antwoord op bovenstaande vraag is zoals gezegd afkomstig van Richard Feynman. Feynman ontwikkelde technieken om zelfs over een oneindig grote (nauwkeuriger: oneindig-dimensionale) ruimte van toestanden een “gemiddelde” te berekenen. Iets meer over de wiskundige techniek waarmee hij dat deed, valt te lezen in dit artikel. Daar valt echter ook te lezen dat de padintegraal-techniek van Feynman, zoals deze methode tegenwoordig wordt genoemd, een benadering is. De techniek werkt alleen exact in heel speciale gevallen; wijkt het daadwerkelijk bestudeerde probleem iets van die speciale gevallen af, dan kunnen we de oplossing alleen benaderen als storingsreeks die beter en beter wordt naarmate de afwijking van het model-probleem kleiner is.
Is dat een groot probleem? In de praktijk niet: door maar genoeg tijd en energie in het berekenen van de padintegraal à la Feynman te stoppen, kunnen we antwoorden berekenen die zo nauwkeurig zijn als we maar willen. Aangezien geen enkel experiment perfect nauwkeurig is, is dat voldoende: theoreten rekenen simpelweg zo ver door dat hun nauwkeurigheid groter is dan die waarmee de experimentatoren meten, waarna theorie en experiment vergeleken kunnen worden.
Voor de wiskundeliefhebbers is daarmee de kous natuurlijk nog niet af. Het zou mooi zijn als we padintegralen op precies dezelfde manier als “gewone” integralen konden uitrekenen, en ook écht de “limiet naar nul” konden nemen. Helaas is dat nog altijd waar de schoen wringt, want het is nog geen enkele wiskundige gelukt om, in navolging van Newton en Leibniz, een dergelijke limiet ook voor algemene padintegralen te definiëren. Hoewel de antwoorden die theoreten vinden dus soms zelfs tot meer dan tien decimalen overeenkomen met wat er uit de experimenten komt, kan nog niemand wiskundig bewijzen dat die antwoorden ook kloppen. Dat zo’n bewijs mogelijk moet zijn, daar twijfelt bijna niemand aan, maar voor de uitvoering ervan moeten we nog even wachten op de volgende Feynman, Newton of Leibniz.
Oplossing van de puzzel van de duizendzijdige dobbelsteen: tel de eerste term (1/1000) bij de laatste term (1000/1000) op: dat geeft 1001/1000. Tel nu de tweede term (2/1000) bij de voorlaatste term (999/1000) op: ook dat geeft 1001/1000. Zo kunnen we doorgaan, tot we de 500e term bij de 501e optellen. Steeds is de som van twee termen 1001/1000; de totale som is dus 500 maal dat antwoord: 500,5. De uitkomst is niet onverwacht: de gemiddelde uitkomst ligt precies midden tussen de kleinste (1) en de grootste (1000) uitkomst in.