Over vogels en vuurvliegjes

Het voorwaartse probleem

Een van de belangrijkste eigenschappen van een natuurwetenschappelijke theorie is haar voorspellende kracht: zijn, gegeven de verzameling vergelijkingen die ons systeem beschrijven, de theoretische voorspellingen in overeenkomst met de realiteit? Als dit keer op keer in verschillende situaties het geval is, en concurrerende theorieën het soms verkeerd hebben, dan worden we steeds zekerder dat onze theorie iets zinvols over de realiteit zegt. Het maken van zulke voorspellingen wordt ook wel het voorwaartse probleem genoemd. Elk voorwaarts probleem kan uiteindelijk worden geformuleerd als een vraag van de vorm: “Gegeven deze wetten, wat voor gedrag kunnen we verwachten?”.

Het inverse probleem

Er is echter nog een tweede soort probleem in de natuurkunde dat dit idee een beetje op zijn kop zet: het inverse probleem. In plaats van te beginnen met een theorie die alle delen van het systeem beschrijft, beginnen we met een observatie van het geheel, zonder losse metingen te doen van de parameters uit een kandidaat-theorie. Uit die observatie proberen we dan terug te redeneren naar de bouwstenen. Een voorbeeld is het zwaartekrachtsveld rond de aarde. Dit wordt in principe bepaald door de precieze dichtheid van onze planeet en de ruimtelijke variatie daarin. Om over de dichtheid van de planeet te leren kunnen we dus het inverse probleem van het zwaartekrachtsveld oplossen. Dit soort inverse problemen leiden tot vragen van de vorm: “Gegeven deze observatie, wat voor onderliggende wetten kunnen we verwachten?”.

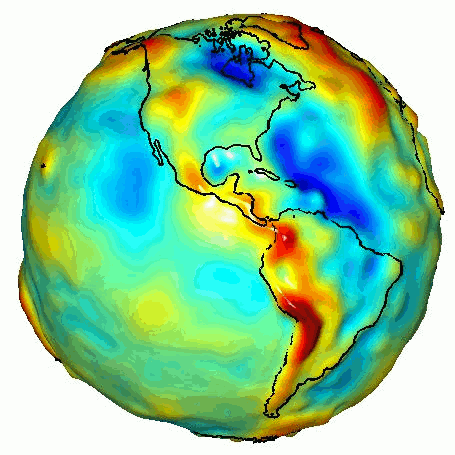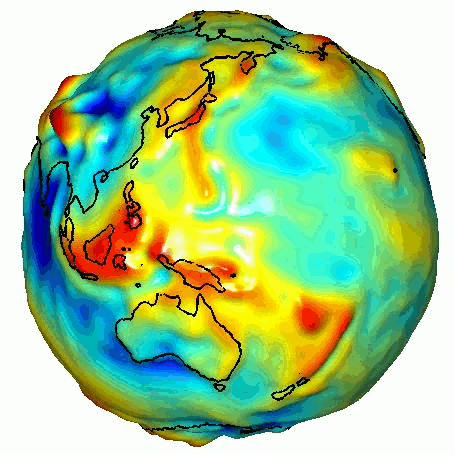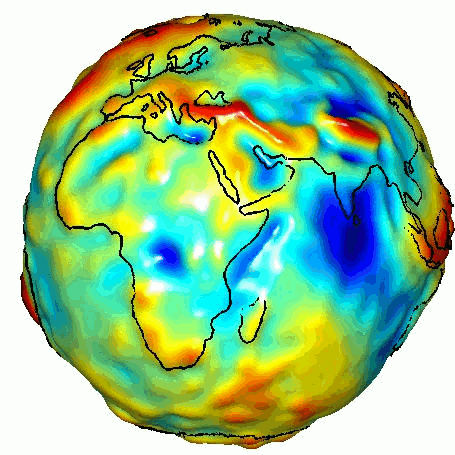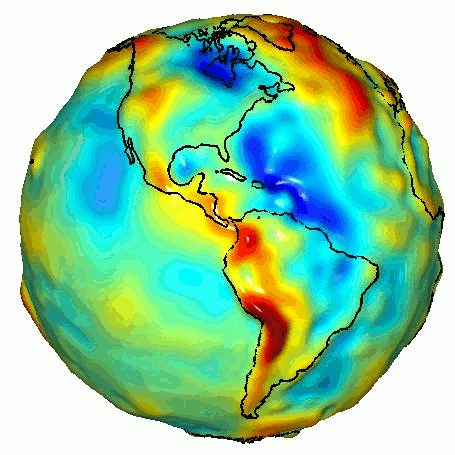
Afbeelding 1. Variatie in zwaartekracht aan het aardoppervlak.Afbeelding: NASA.

Het aardse zwaartekrachtsveld is echter nog een vrij eenvoudig voorbeeld van een invers probleem. We kennen de relevante zwaartekrachtswetten, en hoeven alleen maar de daarin voorkomende dichtheidsparameter af te leiden om het hele inverse probleem op te lossen. Cruciaal is dat elk klein stukje aarde zelf ook al een zwaartekrachtsveld veroorzaakt, onafhankelijk van wat de rest van de aarde doet, en dat het totaal simpelweg de som der delen is.

Emergentie

Een interessantere situatie is die waarin we eigenlijk niet weten welke microscopische variabelen het macroscopische gedrag bepalen. Eigenschappen die zulke systemen op grote schaal hebben, worden emergent genoemd: het gedrag van het systeem als geheel is niet goed te verklaren vanuit eigenschappen van de onderdelen. Dit soort problemen zijn vaak extreem moeilijk op te lossen – er is immers nauwelijks houvast. In tegenstelling tot het zwaartekrachtvoorbeeld zijn we niet alleen op zoek naar de waarde van een bepaalde parameter, maar naar de microscopische wetten zelf. Ook blijkt vaak dat de onderdelen alles behalve onafhankelijk zijn en allerlei interacties met elkaar aangaan.

Een beroemd voorbeeld van emergent gedrag is magnetisme. In 1920 werd door Wilhelm Lenz het zogenaamde Isingmodel geïntroduceerd in de hoop ferromagnetisme – magnetisme zoals we dat in ijzer zien – te verklaren. Het voorwaartse probleem oplossen was hopeloos: er was nog geen goede fundamentele beschrijving van atomen (Schrödinger zou zes jaar later pas zijn beroemde vergelijking publiceren), dus werd het probleem door Lenz benaderd als een invers, emergent probleem. Hij schreef een bepaald soort interacties tussen atomen op en keek of die resulteerden in iets dat leek op magnetisme. Hoe moeilijk dit invers emergente probleem is, blijkt goed uit wat volgde. Lenz liet zijn student Ernst Ising dit probleem onderzoeken, en deze begon met het probleem in één dimensie te bekijken. Ising vond geen magnetisme en concludeerde dat de interacties dus geen magnetisme konden beschrijven. Later bleek echter dat dit alleen geldt voor het ééndimensionale geval waar Ising naar keek, en dat in hogere dimensies dit model, dat nu zijn naam draagt, juist wél magnetisme bevat.

Leven en Complexiteit

Omdat inverse problemen bij relatief eenvoudige systemen zoals atomen al zo moeilijk zijn, is het extra verrassend dat er juist in de biologie een aantal voorbeelden zijn van invers emergente problemen met een eenvoudige oplossing.

Afbeelding 2. Een zwerm spreeuwen.Foto: Tanya Hart.

Het beroemdste voorbeeld is het zwermen van vogels. Een zwerm vogels heeft geen duidelijke leider, maar kan desalniettemin strak gecoördineerde bewegingen uitvoeren, snel van richting veranderen en op roofvogels reageren. Ons gebrek aan kennis over vogelpsychologie dwingt ons om dit zwermgedrag als een invers probleem te benaderen — we kunnen de vogels niet vragen hoe ze het doen, maar kunnen alleen maar het groepsgedrag bekijken. Lang werd gedacht dat dit een erg ingewikkeld probleem was, dat diepe biologische kennis over vogels vereiste. Het was daarom een enorme verrassing toen Craig Reynolds, een computeranimator, in 1987 drie heel eenvoudige regels vastlegde die samen tot het zwermgedrag leiden dat we ook bij vissen en vogels zien. De drie regels zijn:

1. Elke vogel kijkt in zijn naaste omgeving naar de gemiddelde richting van andere vogels, en duwt zijn koers een beetje in die richting.
2. Elke vogel kijkt in zijn naaste omgeving naar de gemiddelde positie van andere vogels, en probeert daar een beetje dichterbij te komen.
3. Als vogels te dicht bij elkaar komen, vliegen ze een beetje uit elkaar.

Het enige wat je nu nog moet doen is bepalen hoeveel “een beetje” is in alle drie de gevallen, maar dat blijkt niet eens zo heel belangrijk om overtuigend zwermgedrag te zien. Een voorbeeld waarin een groepje vogels/vissen deze drie regels volgt, is te zien in de volgende simulatie, waarin ik ook wat “roofdieren” heb gestopt waar de vogels/vissen altijd van weg willen vliegen. (Met de muis kan je meer vogels/vissen toevoegen.)

Wat leren we hiervan? In tegenstelling tot het voorbeeld van het zwaartekrachtsveld, of magnetisme, zijn we hiermee niet veel dichter bij een fundamenteel begrip van het systeem gekomen: we hebben weinig over de hersenen van vogels geleerd. Dit resultaat zegt volgens mij eerder iets over hoe we naar complex emergent gedrag moeten kijken en pleit het voor het serieus nemen van deze meer abstracte dan fundamentele beschrijving van patronen.

Een ander voorbeeld hiervan is synchronisatie. Zeker in de biologie is dit een belangrijk begrip. Vrijwel al het leven op aarde leeft aan de hand van periodieke bewegingen die hun periode, fase en amplitude kunnen variëren als reactie op andere oscillaties. Denk aan leven in het waddengebied en het getij, vogelmigratie en seizoenen, (winter)slapen, hartslag en ademen, etc. Ook hier blijkt het inverse probleem soms een vruchtbare weg naar beter begrip.

Afbeelding 3. Photinus pyralis, een vuurvliegje.Foto: Katja Schulz.

Een prachtig soort synchronisatie is te zien bij vuurvliegjes. Met name in het zuidoosten van Azië zijn er bepaalde vuurvliegjes die ‘s nachts, in groten getale, hun knipperen synchroniseren. Al in het begin van de twintigste eeuw probeerden mensen dit te verklaren, maar omdat dit veel te ingewikkeld gedrag leek voor zo’n eenvoudig beestje werd de verklaring vaak buiten de kever gezocht. Zo werd er bijvoorbeeld gezegd dat het juist de mensen waren die in het donker met hun ogen knipperden, of dat er windvlagen waren die over alle vuurvliegjes heen trokken en zo van buitenaf het synchroniseren afdwongen.

Dat synchronisatie echter niet alleen voort kan komen uit ingewikkelde denkprocessen wordt aangetoond door het volgende experiment, waarin een verzameling metronomen die op een rollende plaat staan uit zichzelf langzaam synchroniseren:

In dit voorbeeld synchroniseren de metronomen door elkaar zetjes te geven via het platform waar ze op staan. Als metronoom 1 een klikje geeft, dan kan hij daarmee via de tafel metronoom 2 net het zetje geven dat hem over de drempel duwt om ook een klikje te geven. Als genoeg metronomen elkaar zo zetjes geven, eindigen ze uiteindelijk allemaal gesynchroniseerd, zelfs als ze allemaal op een iets andere frequentie zijn ingesteld.

Ditzelfde model werkt ook voor vuurvliegjes. Een vuurvliegje kan een keer knipperen, en wacht dan even voordat hij het volgende lichtflitsje produceert. Als elk vuurvliegje op een willekeurig moment begint te knipperen, zou je dus een totaal willekeurig patroon verwachten, zeker als ze niet allemaal even lang wachten tussen de flitsen in. Maar als een lichtflits van een vliegje een ander dichtbij stimuleert om ietsje eerder te knipperen, zou er dus hetzelfde kunnen gebeuren als bij de metronomen. Dit blijkt inderdaad het geval, zoals duidelijk wordt in de volgende simulatie.

Hier laat ik een groep vuurvliegjes rondvliegen en met ongeveer dezelfde periode knipperen. Zoals hierboven beschreven zal een vuurvliegje iets sneller flitsen als hij een naburig vliegje ook ziet knipperen. Na een seconde of twintig beginnen er groepen te ontstaan die tegelijk knipperen, en na ongeveer een minuut knipperen de meeste vliegjes tegelijk. Met de muis kan je nieuwe vuurvliegjes toevoegen om de synchronisatie weer te verstoren. Deze interacties worden vaak beschreven als elektrische circuits die bestaan uit een condensator en een lichtgevoelige weerstand. Het vuurvliegje werkt dan als een batterij die langzaam de condensator oplaadt, en als deze een bepaalde spanning heeft bereikt, een flits afgeeft en de condensator ontlaadt. De lichtgevoelige weerstand in het circuit zorgt er dan voor dat de condensator iets sneller de drempelspanning bereikt als een ander vuurvliegje in de buurt op dat moment flitst.

Onopgelost

Ook dit voorbeeld leert ons niet per se iets over fundamentele biologische onderdelen van een organisme. We weten nog niet precies welke biologische processen deze synchronisatie veroorzaken, en ook niet waarom de vuurvliegjes überhaupt synchroniseren. Toch is het denk ik waardevol om juist zo’n abstracte beschrijving van emergent gedrag te hebben en beter te begrijpen hoe complexe patronen kunnen ontstaan uit relatief eenvoudige interacties.

Veel belangrijke invers emergente problemen blijven tot op de dag van vandaag onopgelost. De beroemdste, en misschien ook wel belangrijkste, is hoge-temperatuursupergeleiding. Het meest directe voorwaartse probleem is daar te moeilijk: we kunnen de fundamentele vergelijkingen die een materiaal beschrijven zelden opschrijven, laat staan oplossen, en onze kans om supergeleiding zo voorwaarts te verklaren lijkt nihil. In plaats daarvan zijn we op zoek naar het soort interacties dat supergeleiding op hoge temperatuur toelaat, in de hoop dat we daar genoeg van leren om ooit materialen te kunnen maken die op kamertemperatuur supergeleidend te zijn.

Zo ver zijn we echter nog niet, en uiteindelijk zijn alle problemen in de natuurkunde een mix van voorwaartse en inverse problemen. Het lijkt me dus wijs om eerst nog zo veel mogelijk te leren van vogels en vuurvliegjes.