
Afbeelding 1. Isaac Newton.Al meer dan drie eeuwen geleden gebruikte Newton gedachte-experimenten om te ontdekken hoe de zwaartekracht werkt. Portret door Godfrey Kneller, uit de National Portrait Gallery in Londen.
Net zoals een foto meer zegt dan duizend woorden, zo is in de natuurkunde het juiste idee vaak meer waard dan duizend formules. De zwaartekrachtswet van Newton zegt bijvoorbeeld dat twee objecten, onafhankelijk van hun samenstelling, tot elkaar aangetrokken worden met een kracht die evenredig is met het product van hun massa’s, en omgekeerd evenredig met het kwadraat van hun onderlinge afstand. Alhoewel je zulke wetten goed in formules kan vatten, zitten er veel ideeën achter die vaak makkelijker te begrijpen zijn aan de hand van een voorbeeld.
Stel je voor dat je een jager bent in een tropisch oerwoud. Voor wetenschappelijk onderzoek moet je een zeldzame orang-oetang vangen. Na dagen zwoegen door het oerwoud sta je eindelijk oog in oog met je prooi: tien meter verder hangt de aap aan een boomtak, recht voor je neus! Je hebt een verdovingsgeweer meegekregen dat slaappijltjes afschiet. De orang-oetang is echter een oplettend dier: zodra je het slaappijltje wegschiet, zal de aap zich laten vallen. Waar moet je mikken om je doel te treffen?
In eerste instantie zou je misschien geneigd zijn om iets onder de aap te mikken, om hem zo in zijn val te onderscheppen. Volgens Newtons wet is dat echter geen goed idee. De aap valt naar beneden door de zwaartekracht van de aarde. Zodra het pijltje uit het geweer komt, valt deze echter net zo goed naar beneden, met dezelfde versnelling als de aap. We komen dus tot de conclusie dat je je pijltje gewoon op de aap zelf moet richten om hem te raken!
In combinatie met de voorwaartse beweging door de kracht uit het geweer levert dit een paraboolbaan op, zoals te zien is in de onderstaande illustratie:
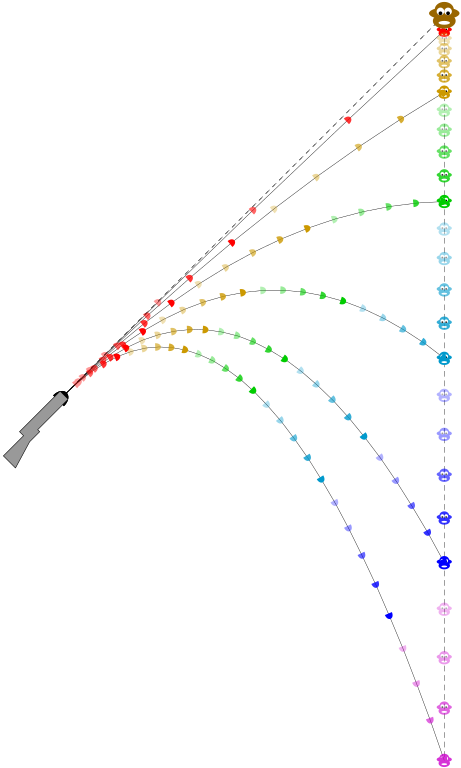
Afbeelding 2. Paraboolbanen.De aap valt met dezelfde versnelling omlaag als het pijltje dat we afschieten. Of we de pijl dus hard (rood) of zacht (blauw) schieten, we moeten gewoon mikken op de plek waar de aap op dit moment hangt! Afbeelding: Wikipedia-gebruiker Cmglee.
Laten we nu iets zwaarder geschut in stelling brengen. Stel je voor dat je het voor elkaar gekregen hebt om een kanon op de top van een enorm hoge berg te zetten, vanwaar vrij zicht op de weidse omgeving is. Als je het kanon afschiet, verplaatst de kogel zich naar voren, om uiteindelijk net als de pijl met een paraboolbaan op de flank van de berg landen.
Met flink wat meer kruit in het kanon kan de kogel misschien wel in het dal aan de voet van de berg komen. Echter, met een uiterst krachtig kanon zou je de kogel zó ver kunnen schieten dat de kromming van de aarde merkbaar wordt. Volgens Newtons zwaartekrachtswet valt de kogel dan niet langer in een paraboolbaan maar in een ellipsbaan. Op een zeker moment zal de kogel zo veel horizontale snelheid hebben dat hij in een baan om de aarde terechtkomt. De zwaartekracht van de aarde is dan niet meer voldoende om de kogel terug op aarde te laten komen: de kogel gaat in een baan om de aarde bewegen. Het was Newton zelf die inzag dat dit precies is wat er met onze maan gebeurt: die ‘valt’ continu om de aarde heen. Dezelfde zwaartekracht die verantwoordelijk is voor het vallen van het pijltje en de orang-oetan, zorgt dus ook voor de baan die de maan om de aarde beschrijft! In Newtons tijd was dit een baanbrekend nieuw inzicht. Met nóg meer kracht is het overigens natuurlijk ook mogelijk om de kogel van de aarde te laten ontsnappen, net als een ruimtesonde.
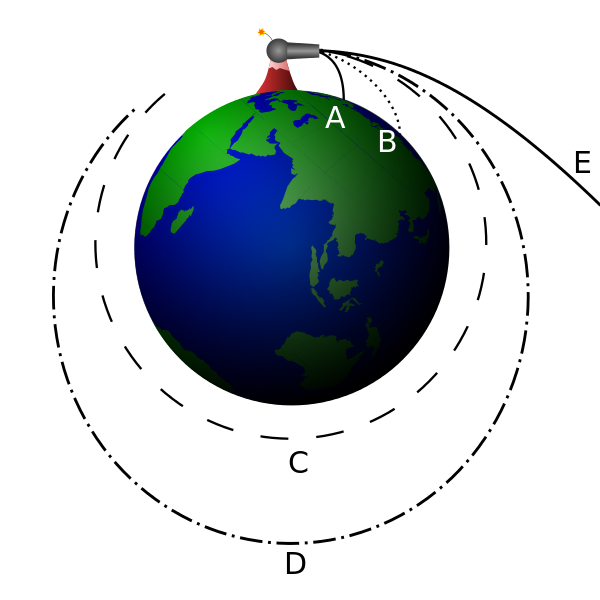
Afbeelding 3. Kogelbanen.Wanneer je een kogel maar hard genoeg wegschiet, zal die nooit meer op de aarde terugvallen. Afbeelding: Brian Brondel.
Al deze observaties volgen na enige wiskunde uit de zwaartekrachtswet van Newton. Hoewel de wiskunde van Newton voor zijn tijd revolutionair was, is het grote natuurkundige inzicht misschien nog wel indrukwekkender. Het feit dat Newton zulke verschillende fenomenen, van de banen van de planeten om de zon tot de trajecten van projectielen op aarde, kon beschrijven met één enkele formule, was een ware revolutie in het wetenschappelijk denken. Situaties als de vorige twee voorbeelden, die moeilijk praktisch uit te voeren zijn maar wel fundamentele inzichten kunnen illustreren, noemen we ook wel ‘gedachte-experimenten’. Zulke hypothetische experimenten vormen een belangrijk hulpmiddel in het uitbreiden van de grenzen van de theoretische natuurkunde.
Ook in de wiskunde zijn gedachte-experimenten een dankbaar gereedschap om moeilijk te vatten concepten helder te maken. Oneindigheid is een berucht voorbeeld van zo’n moeilijk concept, en al eeuwenlang worstelen mensen met de verwarrende situaties die eruit voorkomen. Hier kan een gedachte-experiment aan de ene kant helpen om verkeerde intuïtie bloot te leggen, en aan de andere kant zelfs bovendien tot heel nieuwe concepten leiden. Het volgende gedachte-experiment is afkomstig van de Duitse wiskundige David Hilbert.

Afbeelding 4. Hilberts hotel.Hilbert gebruikte voor zijn gedachte-experiment een oneindig groot hotel. Foto: Wikipedia-gebruiker Traveler100.
Stel dat je een hotel runt op een gewilde locatie in de bergen. Het hotel bestaat uit een balie bij de ingang, gevolgd door een lange gang met vijftig kamers aan elke zijde. Het is hoogseizoen, en alle honderd kamers zijn bezet. Elke gast die nu nog aanklopt, zul je helaas moeten teleurstellen.
Echter, wat nu als de gang geen einde heeft? Wat als er oneindig veel kamers zijn? In dat geval is er een heel simpele methode om één extra gast te huisvesten, zelfs als alle kamers bezet zijn. Je vraagt simpelweg de gasten uit de eerste kamer te verhuizen naar de tweede kamer, die van de tweede kamer naar de derde, enzovoort. Alle oude gasten houden onderdak en de nieuwe gast kan in kamer één aansluiten.
Sterker nog, er zouden zelfs oneindig veel nieuwe gasten bij kunnen. Vraag de gasten uit kamer één naar kamer twee te vertrekken, stuur kamer twee naar kamer vier, kamer drie naar kamer zes, et cetera. Alle kamers met even nummers zijn nu bezet door oude gasten, maar alle oneven kamers zijn vrij. Aangezien er zowel oneindig veel even als oneindig veel oneven kamers zijn, kunnen er nu oneindig veel nieuwe gasten bij.
Wiskundig gezien is hier niets geks aan de hand. Als we dit experiment nog een stapje verder doorvoeren, komen we echter op moeilijkheden uit. Stel dat we met een leeg hotel beginnen en de gasten een nummertje moeten trekken in een oneindig lange rij aan kaartjesautomaten. Elke automaat geeft een getal tussen 0 en 9 en de gast vormt met alle cijfers die hij krijgt een getal tussen 0 en 1. Voor een gast die een 4 en een 6 trekt begint dit getal bijvoorbeeld met 0,46… Een gast die een 4, een 6 en vervolgens alleen maar nullen trekt komt dus precies op het getal 0,46 uit en mag naar kamer 46. Een gast die een 4, een 6 en een 3 gevolgd door nullen trekt krijgt 0,463 en slaapt in kamer 463. Echter, een gast die een 4, een 6, een 2 en vervolgens alleen maar negens trekt maakt het getal 0,4629999… Maar dat is hetzelfde als 0,463, dus deze gast mag óók aanspraak maken op kamer 463. En naar welke kamer mag de gast die bijvoorbeeld 0,33333333… trekt? Het oneindig grote hotel is te klein geworden!
Wat is hier aan de hand? Om alle mogelijke kaartcombinaties te laten voorkomen, moeten we meer oneindig veel gasten aantrekken dan dat er kamers zijn. In wiskundige termen zijn er aftelbaar veel kamers aan de gang, terwijl er overaftelbaar veel getallen tussen 0 en 1 te verdelen zijn.Wil je een wiskundig bewijs zien van het feit dat het écht nooit gaat passen, kijk dan het onderstaande filmpje:
Met deze methode komen er dus een grotere oneindige hoeveelheid gasten naar het hotel dan dat er kamers zijn. Zulke afwegingen leidden wiskundigen, waaronder de Duitse Georg Cantor, tot een theorie van verschillende soorten oneindigheden, puur en alleen aan de hand van theoretische overpeinzingen.
Gedachte-experimenten kunnen ons dus aan de ene kant in staat stellen om intuïtie te kweken of voorspellingen te doen voor echte experimenten. Aan de andere kant kunnen we ook op geheel nieuwe concepten stuiten, zonder dat deze ooit door een natuurlijk fenomeen gemotiveerd zijn. Al met al zijn gedachte-experimenten een onmisbaar hulpmiddel in de wiskunde en theoretische natuurkunde! In het vervolg van deze serie zullen we nog veel meer voorbeelden van dit mooie gereedschap tegenkomen.