
Afbeelding 1. Een quantumcomputer.IBM quantumcomputer gebaseerd op supergeleidende qubits. Een groot probleem voor quantumcomputers is hun instabiliteit: de structuur die de quantumbits hebben vervalt binnen (een paar) seconden. Dit komt door ongewenste interacties met de omgeving. Dergelijke machines zijn een goed voorbeeld van een quantummechanisch systeem waarbij dissipatie een belangrijke rol speelt. Foto: IBM.
Er wordt veel geschreven over de quantummechanica en toepassingen van die theorie in onze moderne samenleving. Daar is een goede reden voor: quantummechanica is verreweg de meest nauwkeurige theorie die we hebben voor de natuur. De theorie is getest op de meeste manieren, en op de meeste verschillende energieschalen (heel koud, en heel heet).
De bedenkers van de quantummechanica baseerden hun oorspronkelijke ideeën natuurlijk op experimenten, maar formuleerden al gauw ook de grondregels van de theorie. Deze grondregels, of axioma’s, zijn eigenlijk vrij eenvoudig. Een van deze axioma’s is het behoud van kansen: de kans dat er íéts gebeurt is 100%, dus gelijk aan één. Dit is vervolgens weer gelinkt aan een andere belangrijke natuurwet: het behoud van energie. Deze wet is onaantastbaar. Er zijn daarentegen wel systemen die energie uitwisselen met de omgeving en dus op zichzelf zich niet houden aan deze regel van behoud van energie. Denk aan aangedreven en verdampende systemen. Systemen die energie uitwisselen met hun omgeving, en die daardoor zelf niet in een thermodynamisch evenwicht zijn, noemen we dissipatief. In de praktijk zijn zulke systemen eigenlijk de meest reële systemen die we kunnen bedenken: in onze dagelijkse wereld verwarmen we steeds allemaal voorwerpen, om ze vervolgens af te laten koelen. Dit betekent dat voor het systeem in kwestie energie niet behouden is. Uiteraard is voor het dissipatieve systeem en de omgeving als geheel energie wel behouden.
Neem bijvoorbeeld een verbrandingsmotor: we stoppen er constant energie in, in de vorm van ontploffende benzine, en laten het ontstane gas vervolgens afkoelen waarbij we arbeid winnen voor beweging. De theorie voor dit soort motoren is vrij goed bekend, en in klassieke thermodynamica kan goed met dit soort systemen omgegaan worden. Nu kan je je afvragen: hoe werken zulke systemen in de quantumwereld? Daar komen dergelijke systemen ook zeer vaak voor. Dat is met name het geval bij interacties tussen materie en lichtvelden, zoals we veel zien in laboratoria wanneer we lasers gebruiken om atomen in een gewenste toestand te krijgen. Ook zien we quantumsystemen waarin energie niet behouden is opduiken bij de bouw van quantumhardware, zoals het apparaat in afbeelding 1.
Dit artikel gaat over de theorie van systemen die niet in evenwicht zijn met hun omgeving, en de implicaties daarvan. Het artikel is opgesplitst in twee delen: het eerste deel geeft een korte crash course in hoe men over het algemeen een quantummechanisch probleem aanpakt, en hoe dit uiteindelijk leidt tot de vergelijkingen die we nodig hebben voor speciale dissipatieve systemen. Het tweede deel vertelt over de implicaties en toepassingen van deze dissipatieve systemen.
Deel 1: Een crash course in dissipatieve quantummechanica
Quantummechanica heeft eigenlijk een heel eenvoudig stappenplan:
Stap 1: Schrijf de Schrödingervergelijking op:
\(-i\hbar \frac{d}{dt} \psi = H \psi\)
Stap 2: Los die vergelijking op om een golffunctie te vinden.
De Schrödingervergelijking (hierboven ter illustratie weergegeven, maar de precieze wiskunde is voor ons verhaal niet van belang) vertelt ons hoe een quantummechanisch object zich zal gaan gedragen in de loopt van de tijd. Als we die opgelost hebben, dan vinden we de golffunctie van dat quantummechanisch object. Die golffunctie is een wiskundige functie die een beschrijving geeft van het volledige gedrag van het quantummechanische object.
We kunnen deze methode uitbreiden naar de situatie die voor dissipatieve systemen van belang is: het geval dat we veel deeltjes tegelijk beschrijven. Dan zoeken we niet de golffunctie van één object, maar de golffunctie van een hele reeks objecten tegelijkertijd. Als het lukt om de Schrödingervergelijking op te lossen vinden we één golffunctie van een groot aantal variabelen die bijvoorbeeld de toestand van een hele reeks atomen tegelijkertijd beschrijft. De Schrödingervergelijking wordt in dit geval wel exponentieel ingewikkelder om op te lossen. Desondanks is de studie van zulke oplossingen een zeer interessant vakgebied. Het staat namelijk in direct contact met materiaalkunde. Zo kan je met zulke golffuncties metaalroosters bestuderen om daar nieuwe eigenschappen in te ontdekken. Dit leidt ook naar ‘spannendere’ onderwerpen zoals supergeleiders (geleidende materialen die geen weerstand hebben) of topologische isolatoren.
Tot nu toe lijkt het alsof we een heel eind kunnen komen. Wat ik alleen nog niet verteld heb, is dat de Schrödingervergelijking eigenlijk niet compleet is: die geeft ons alleen maar de dynamica van een quantummechanisch object in een zogeheten zuivere toestand. De term toestand’ betekent hier zoiets als: ‘de situatie waarin onze meerdere-deeltjes-golffunctie zich bevindt’. Een zuivere toestand is misschien het makkelijkst te begrijpen door te kijken naar zijn tegenpool, een gemengde toestand.
Intermezzo: gemengde en zuivere toestanden
De quantummechanica kent maar liefst twéé soorten kansbegrip. Allereerst zijn er de gewone kansen zoals in ons dagelijks leven: vaak weten we van een systeem niet precies in welke toestand het is, en beschrijven we onze onwetendheid met een kansverdeling – de kans is 10% dat het systeem in deze toestand in, 20% dat het in die toestand is, enzovoort. Een dergelijke ‘toestand van onwetendheid’ noemen we in de quantummechanica een gemengde toestand.
Mogelijk verwarrend is dat er in de quantummechanica hiernaast nog een heel speciaal soort ‘kansen’ bestaat: zelfs als we over een quantumsysteem namelijk álles weten, is het nog vaak zo dat we niet de uitkomst van een experiment kunnen voorspellen, maar alleen de kansen op verschillende uitkomsten. In het geval waarin we van een quantumsysteem alles weten wat we kúnnen weten, spreken we van een zuivere toestand. Daarbij is er dus nog steeds sprake van kansen, maar nu kansen die ontstaan uit onbepaaldheid, niet uit onwetendheid.
We moeten onze Schrödingervergelijking dus upgraden naar een vergelijking die daadwerkelijk álle quantumtoestanden kan beschrijven. Deze formule staat bekend als de Liouville-von Neumann vergelijking. De vergelijking heeft dezelfde ingrediënten nodig als de Schrödingervergelijking, maar is iets anders opgebouwd, waardoor niet alleen pure toestanden, maar ook gemixte toestanden beschreven kunnen worden. De wiskundige formulering wordt daarmee wel ingewikkelder. In plaats van een ‘golffunctie’ die de vorm heeft van een vector, beschouwen we nu een ‘dichtheidsmatrix’. Over wat matrices precies zijn kun je meer lezen in deze serie artikelen van Jeremy van der Heijden. De dichtheidsmatrix is een tegenhanger van een golffunctie voor het geval waarin we zowel pure als gemixte toestanden willen beschrijven. Als we dus een algemener quantummechanisch probleem willen oplossen moeten we dus eigenlijk de volgende stappen doorlopen:
Stap 1: schrijf de Liouville-von Neumannvergelijking op:
\(\frac{d}{dt}\rho = -i [H,\rho]\)
Stap 2: los die vergelijking op om de dichtheidsmatrix te vinden.
Een toepassing voor deze vergelijking vinden we bijvoorbeeld in de laserfysica. Met behulp van het bovenstaande formalisme is het mogelijk om te bepalen welke krachten een atoom ondervindt in een laserveld; iets wat niet mogelijk is met de normale Schrödingervergelijking. Deze kennis is van vitaal belang om te beschrijven hoe men een atoom kan laten zweven in een optische val, zoals aangegeven in de serie over het maken van ultrakoude gassen.
Met de Liouville-von Neumannvergelijking kunnen we in principe de wereld om ons heen beschrijven. Als we dat letterlijk voor de hele wereld willen doen, zouden we wel enorm veel informatie nodig hebben om de vergelijking op te lossen. Dat is natuurlijk onmogelijk. Wat we dus doen is niet het hele universum tegelijkertijd beschrijven, maar alleen dat object wat ons interesseert. Dit reduceert onze benodigde informatie tot iets behapbaars en brengt ons direct naar het oorspronkelijke doel van dit artikel: de vraag hoe een aangedreven of dissiperend quantummechanisch systeem werkt. De volgende afbeelding geeft een schematisch beeld van ons probleem:
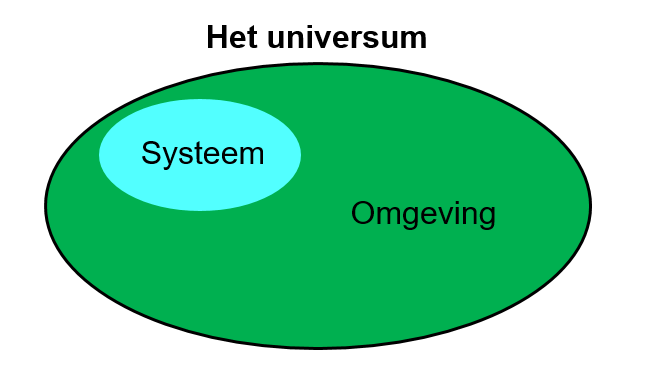
Afbeelding 2. Systeem en omgeving.Het universum is opgebouwd uit twee delen: het systeem wat ons interesseert, en de rest: ‘de omgeving’.
Het idee is dat we de Liouville-von Neumann vergelijking gebruiken, maar dan op een slimme manier alle informatie van de omgeving wegfilteren, zodat we alleen een effectieve formule overhouden die ons systeem beschrijft. Voor dat systeem is er dus geen energiebehoud. Het kan immers warmte of andere vormen van energie ontvangen van en afstaan aan zijn omgeving.
In de jaren 70 heeft de Zweedse natuurkundige Göran Lindblad bewezen dat alle vergelijkingen die het gedrag van dissipatieve systemen beschrijven, geschreven kunnen worden in een bepaalde vorm: de zogeheten Lindbladvergelijking. Deze vergelijking is dus voor zulke systemen het equivalent van de Schrödingervergelijking en vertelt ons exact wat er gebeurt voor ons specifieke systeem, voor zowel zuivere als gemengde toestanden. Er is wel een belangrijke voorwaarde om deze vergelijking te kunnen toepassen: het contact met de omgeving moet heel snel en soepel kunnen verlopen. Oftewel: als er energie weglekt naar de omgeving, dan is die energie weg uit het systeem, en kan niet meer terugkomen. Daarnaast mag de weggelekte energie de eigenschappen van de omgeving niet veranderen. Een typisch voorbeeld dat aan die eisen voldoet kwamen we ook eerder tegenin dit artikel: een atoom dat beschenen wordt door een laser. Het lichtveld van de laser functioneert als de ‘omgeving’ in afbeelding 2. Als het atoom een foton uitzendt, zal dit foton wegvliegen en het systeem verlaten. Daarnaast zal het ook het licht van de laser, en dus de omgeving, niet aanpassen.
De Lindbladvergelijking ziet er als volgt uit:
\(\frac{d}{dt}\rho = -i [H,\rho] + \mathcal{D} \rho\)
In woorden zegt de vergelijking het volgende: de tijdsevolutie van ons systeem wordt bepaald door een vergelijking zoals een Liouville-von Neumannvergelijking die we hierboven zagen plus een extra stuk, de term met de ‘D’. De factor ‘D’ bepaalt de interactie van ons systeem met de omgeving. In figuur 2 beschrijft deze vergelijking dus de evolutie van de blauwe bol, en ‘D’ vertelt hoe het blauw samenwerkt met het groen.
Deel 2: Dynamische fasen in quantummechanica
Het blijkt dat dynamisch aangedreven, dissipatieve systemen zeer exotische fase-overgangen vertonen, die niet voorkomen in de evenwichtsnatuurkunde zoals we zien in klassieke thermodynamica en quantummechanica. Wellicht is het leuk om te weten dat de theorie van dissipatieve systemen niet alleen maar ongewone toestanden voorspelt in allerlei natururkundige systemen, maar ook in de socio-economie en biologie, waar dergelijke niet-evenwichtssystemen meer norm dan uitzondering zijn.
In evenwichts-thermodynamica en, in zekere mate, in quantummechanica is vrij goed bekend hoe we de eigenschappen van een systeem kwalitatief kunnen beschrijven. Het blijkt zelfs dat faseovergangen van een (klassiek, thermodynamisch) materiaal zich vrijwel allemaal op een vergelijkbare manier gedragen. Een fenomeen dat ook wel ‘universaliteit’ wordt genoemd.
Voor dissipatieve systemen is een dergelijke eigenschap niet bekend – over deze systemen is sowieso nog weinig bekend. In het algemeen kijken we bij het bestuderen van zo’n systeem naar wat we noemen de ‘dissipative gap’. Dit is een maat voor de tijd die het ons systeem kost om te vervallen naar een bepaalde toestand die de ‘non equilibrium steady state’ wordt genoemd. Hoe groter de ‘gap’, hoe sneller het systeem vervalt. Vrijwel elk dissipatief systeem dat we kennen vervalt uiteindelijk naar een dergelijke toestand. De precieze eigenschappen van dit verval zijn echter kenmerkend voor het materiaal. Een typisch voorbeeld van een dynamisch aangedreven, dissipatieve faseovergang is de situatie zijn waarbij je, door de parameters van een systeem (meestal de sterkte van een magnetisch veld) te vaiëren, de ‘dissipative gap’ kan ‘sluiten’. Dit heeft als gevolg dat de dynamica van het systeem ineens heel langzaam wordt, of misschien zelfs volledig verdwijnt, om vervolgens weer te verschijnen, maar dan met een andere karakteristieke eigenschappen. Denk bijvoorbeeld aan de mogelijkheid om naar toestanden te vervallen die er eerst niet waren. Het is mogelijk om de verschillende fases van dergelijke systemen in een zogeheten ‘fasediagram’ te brschrijven. Dergelijke diagrammen zijn technisch en verder weinig illustratief; het volstaat om te weten dat als men gaat draaien aan de knop voor bijvoorbeeld magneetveldsterkte, het mogelijk is om de stabiliteit van het systeem te veranderen.
Toepassingen voor quantumcomputers
Het directe nut van de methodes die ik hierboven beschreven heb is immers niet eenvoudig te zien. Daarom sluit ik af met een aantal voorbeelden waar deze technieken een belangrijke rol spelen. Een vrij specifiek, maar zeer belangrijk voorbeeld komt voor in de optische natuurkunde. Het is overigens leuk om te weten dat het vakgebied van dissipatieve systemen ook zijn oorsprong vindt in de quantumoptica. De afbeelding hieronder geeft een schematische weergave van, zoals dat heet, een twee-levelsysteem. Je ziet een atoom dat in twee toestanden kan zijn, weergegeven door de onderste lijn in de inzet van de figuur en de bovenste lijn. Dit atoom wordt vastgehouden in een ‘optical cavity’. Een laser kan gebruikt worden om het systeem in de gewenste toestand te krijgen (bijvoorbeeld die met de hoogste energie), maar door ongewenste interacties met de omgeving zal het atoom op den duur toch spontaan vervallen naar de toestand met de laagste energie. Hoe groter de ‘dissipative gap’, hoe eerder dit verval gebeurt. Dergelijke systemen van atomen zijn prototypes van qubits die in quantumcomputers gebruikt worden. Onder meer aan de UvA wordt onderzoek gedaan naar het gebruik van zogeheten Rydbergatomen (atomen die in speciale toestanden geprepareerd worden met behulp van lasers) als qubits. In laboratoria waar in experimenten atomen vastgehouden worden en beïnvloed worden met lasers is gebleken dat een goed begrip van de theorie van dissipatieve systemen van vitaal belang is voor een goed functionerend experiment.
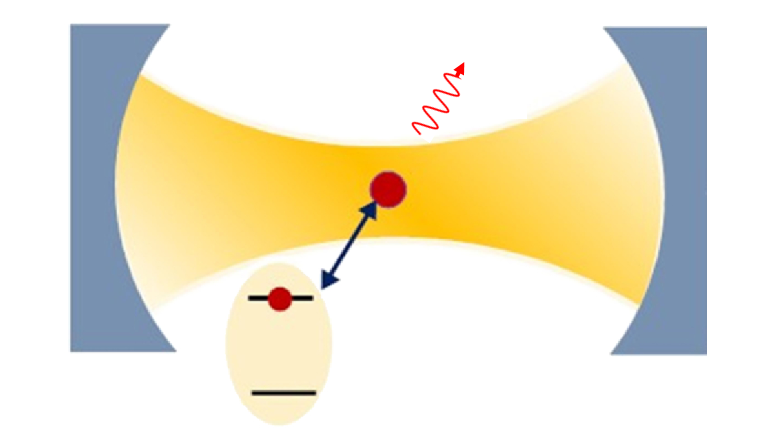
Afbeelding 3. Een twee-levelsysteem.Een schematische weergave van een twee-levelsysteem dat opgesloten is in een ‘optical cavity’, waarbij een atoom zich bevindt tussen twee kromme spiegels waarin licht ‘opgesloten’ is (voortdurend heen en weer kaatsend op beide spiegels). De rode pijl naar rechts boven impliceert spontaan verval van het atoom, wat meestal een ongewenst proces is, en wat we proberen te begrijpen met behulp van de Lindbladvergelijking.
Qubits zijn uiteraard van vitaal belang als het gaat over het ‘hot topic’ van quantumcomputers (zie afbeelding 1). Quantumcomputers zijn zoals gezegd machines die hun rekenkracht niet halen uit gewone bits, maar uit hun quantummechanische tegenhanger: qubits. Deze machines zouden een geweldige sprong in rekenkracht kunnen bewerkstelligen en allemaal fantastische dingen kunnen waarmaken voor de wetenschap en de maatschappij. Eén van de grote uitdagingen voor het bouwen van een quantumcomputer is het verval van de qubits. Atomen (die de qubits vormen) die in een bepaalde toestand zijn gebracht, wat nodig is voor berekeningen, zullen op den duur vanzelf vervallen naar een andere toestand. Dit proces is niet tegen te houden, het zal hoe dan ook gebeuren. Het verval gebeurt namelijk doordat het atoom ondanks isolerende maatregelen, toch contact heeft met zijn omgeving. We kunnen het gewoonweg niet perfect daarvan afsluiten. En dan is er ook nog het contact met het lichtveld, of andere signalen, waarmee een atoom in een supercomputer zou worden aangestuurd. Het verval van de qubits moet dus begrepen worden, zodat men wellicht een manier vind om deze ongewenste processen de kop in te drukken.
Dit brengt ons weer terug naar de fases van dissipatieve systemen. Als we willen kunnen beïnvloeden hoe lang atomen stabiel zijn voor ze vervallen, is een groot begrip nodig van de verschillende toestanden van een atoom in contact met zijn omgeving. Hiervoor zijn formules zoals de Lindbladvergelijking een heel nuttig gereedschap. De kennis die we hiermee opdoen zou ons uiteindelijk kunnen helpen om in de toekomst echte quantumhardware te maken.