Stel je eens voor: het is de zeventiende eeuw en je ligt ’s avonds op bed te peinzen over het universum. Je weet dat de gangbare opvatting is dat het heelal oneindig oud en groot is, en niet verandert – kosmologen noemen dat een ‘statisch’ heelal. Verder lijkt het je logisch dat de sterren in het heelal homogeen verdeeld zijn over de ruimte. Wat hebben deze eigenschappen van het heelal tot gevolg? Als het heelal oneindig groot is en de sterren homogeen verspreid zijn, dan zijn er ook oneindig veel sterren. Er zou, waar je ook precies kijkt, altijd een ster in jouw gezichtslijn moeten staan. Maar dan is er dus waar je ook kijkt een lichtpuntje: het kan niet donker zijn in zo’n heelal! Je springt op van je bed en kijkt naar buiten: het is donker. Wat concludeer je?
Afbeelding 1. Heinrich Wilhelm Olbers (1758-1840).Heinrich Olbers, naar wie de “dark night sky paradox” is vernoemd. Het probleem was echter al aan het begin van de zeventiende eeuw geformuleerd. Lithografie van Rudolph Suhrlandt.
Op die laatste vraag zijn verschillende antwoorden mogelijk, maar duidelijk is in elk geval dat je aannames over het heelal niet allemaal juist kunnen zijn. Dit probleem staat bekend als Olbers’ paradox, naar de amateurastronoom Heinrich Wilhelm Olbers (overigens niet de eerste die hierover schreef). Laten we, voor we naar oplossingen van de paradox kijken, nog iets preciezer beargumenteren waarom het altijd licht zou moeten zijn in een statisch, oneindig oud heelal. We moeten immers ook rekening houden met het feit dat sterren die verder weg staan minder lichtopbrengst geven. Verdeel het heelal om je heen in gedachten in allemaal bolschillen van gelijke dikte, bijvoorbeeld één lichtjaar. Stel dat er in de schil tussen 1000 en 1001 lichtjaar van ons weg een miljoen sterren zitten. Het volume in de schil tussen 2000 en 2001 lichtjaar is vier keer zo groot en bevat dus (als de sterren homogeen verdeeld zijn over het heelal) vier miljoen sterren. Maar: de lichtkracht van een ster neemt kwadratisch áf met de afstand, en is voor deze sterren dus vier keer zo klein. Beide effecten heffen elkaar precies op, dus uiteindelijk is de totale lichtopbrengst per schil gelijk. In een oneindig groot, oud heelal ontvangen wij licht van oneindig veel van die schillen, en dus zou de hemel oneindig verlicht zijn.
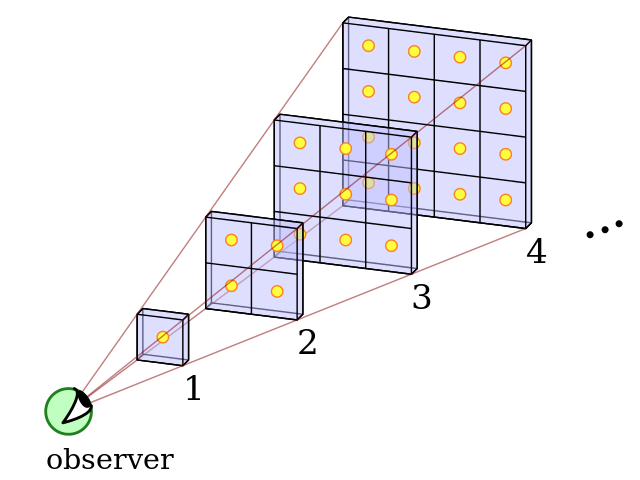
Afbeelding 2. Meer en meer sterren.Het aantal sterren per schil neemt kwadratisch toe met de afstand. De lichtkracht per ster neemt echter kwadratisch af met de afstand… en dus is de lichtopbrengst per schil gelijk! Afbeelding: Wikipedia-gebruiker Htkym.
Een voor de hand liggende oplossing voor Olbers’ paradox is dat we simpelweg (nog) niet alle sterren kunnen waarnemen. Hoe zou dat kunnen? Als het heelal niet oneindig oud is en de lichtsnelheid eindig, dan heeft het licht van verre sterren nog niet genoeg tijd gehad om ons te bereiken en is het dus, op het licht van de sterren die dichtbij genoeg staan na, donker. Hoewel het heelal in deze oplossing nog steeds oneindig groot kan zijn, is het waarneembare heelal dat niet. Grappig genoeg was het overigens de dichter Edgar Allan Poe die in 1848 in het essay Eureka als een van de eersten in die richting dacht:
Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy – since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all.
Binnen het huidige model van het heelal – het oerknalmodel – wordt de donkere nacht mede verklaard door een van de andere aannames los te laten: het heelal is niet statisch, maar dynamisch. Dat leidt in eerste instantie tot een nieuwe paradox. Het universum was kort na de oerknal namelijk ontzettend licht (elk punt aan de hemel had toen een helderheid vergelijkbaar met die van het oppervlak van de zon), en als we nu ver weg in het heelal kijken (en dus terug in de tijd) komt onze gezichtslijn meestal uit in die overblijfselen van de oerknal: het zou wéér overal licht moeten zijn! Dit keer biedt de uitdijing van het heelal de oplossing: daardoor heeft al het licht een zogeheten roodverschuiving gekregen, waardoor het een (veel) lagere energie krijgt. Dit is vergelijkbaar met het dopplereffect dat optreedt als een ambulance langs komt: de frequentie (en dus de energie) van het geluid verandert als de auto naar je toe of van je weg rijdt.
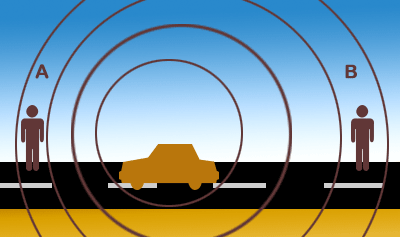
Afbeelding 3. Het dopplereffect. Als een auto of ambulance van je af beweegt (B), wordt de golflengte van het geluid groter, en daarmee de frequentie (en dus de energie) lager. Hetzelfde gebeurt met het licht van sterren die van ons af bewegen: de frequentie (energie) wordt lager. Afbeelding: Zappys Technology Solutions.
We zien dus wel nog een overblijfsel van die enorme lichtintensiteit, maar dan met veel lagere energie: de kosmische achtergrondstraling. Die is echter bij lange na niet voldoende om ons tijdens onze avondwandeling bij te kunnen oriënteren: er komt net zo veel licht vanaf als van een object dat gloeit met een minuscule temperatuur van 2,75 Kelvin – zo’n -270 graden Celsius!
Hoewel je dit feit en het oerknalmodel misschien niet zomaar tijdens je nachtelijke overpeinzingen had kunnen bedenken, blijft het indrukwekkend hoeveel we kunnen afleiden uit de simpele constatering dat het ’s avonds donker wordt. Een goede reden om ’s nachts naar de sterren te staren en over het heelal na te denken!