
Kunstmatige neurale netwerken
Een neuraal netwerk is een verzameling van onderling verbonden knooppunten die signalen met elkaar kunnen uitwisselen. Zulke netwerken vind je in het bijzonder terug in het menselijk brein, waar zenuwcellen (neuronen) door synapsen met elkaar verbonden zijn. Kunstmatige neurale netwerken zijn wiskundige modellen die geïnspireerd zijn op deze biologische structuur. De neuronen worden nagebootst door kunstmatige eenheden die bepaalde waardes aan kunnen nemen, en de synapsen worden gerepresenteerd door verbindingen tussen deze eenheden.
De netwerkstructuur wordt gebruikt om computersoftware te maken die bepaalde vaardigheden van het menselijk brein nabootst. In tegenstelling tot traditionele computersoftware, die opereert op basis van heldere, vooraf vastgelegde instructies, kunnen neurale netwerken door middel van voorbeelden getraind worden. Hierdoor kunnen ze bepaalde taken uitvoeren die te ingewikkeld of te vaag zijn om in stap-voor-stap instructies te vertalen. Nobelprijswinnaars Hopfield en Hinton maakten gebruik van natuurkundige principes om neurale netwerken te ontwerpen die informatie kunnen reconstrueren en interpreteren.
Het Hopfield-netwerk
Stel je voor dat je slechts een deel van een liedje hoort. Automatisch vul je het lied in gedachten aan, denk je aan andere nummers van dezelfde artiest, of herinner je je het concert waar je bent geweest. Dit zijn allemaal voorbeelden van associaties. Je staat er misschien niet bij stil, maar dit soort associaties vinden continu plaats in je hersenen en zijn cruciaal voor de werking van je geheugen. Geïnspireerd door dit proces publiceerde John Hopfield in 1982 een artikel over een een neuraal netwerk dat het associatieve geheugen imiteert. Het Hopfield-netwerk kan patronen opslaan en, als het vervolgens een incompleet of vervormd patroon voorgeschoteld krijgt, zoeken naar het opgeslagen patroon dat daar het meest op lijkt.
De werking van het Hopfield-netwerk is gebaseerd op natuurkundige principes die gelden in magnetische materialen. Magnetisme in deze materialen is een gevolg van de spin van de elektronen, een eigenschap waardoor die elektronen zich gedragen als een soort kleine magneetjes. De spin van een elektron wordt beïnvloed door de spin van naburige elektronen, waardoor gebieden van elektronen met dezelfde spin ontstaan. Hopfield realiseerde zich dat zenuwcellen in de hersenen elkaar op een vergelijkbare manier beïnvloeden en ontwierp een kunstmatig netwerk dat dit gedrag imiteert.
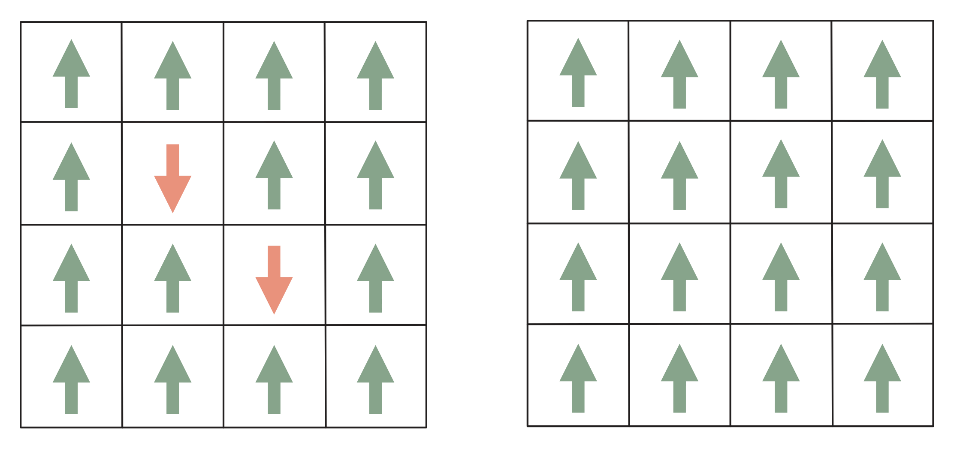
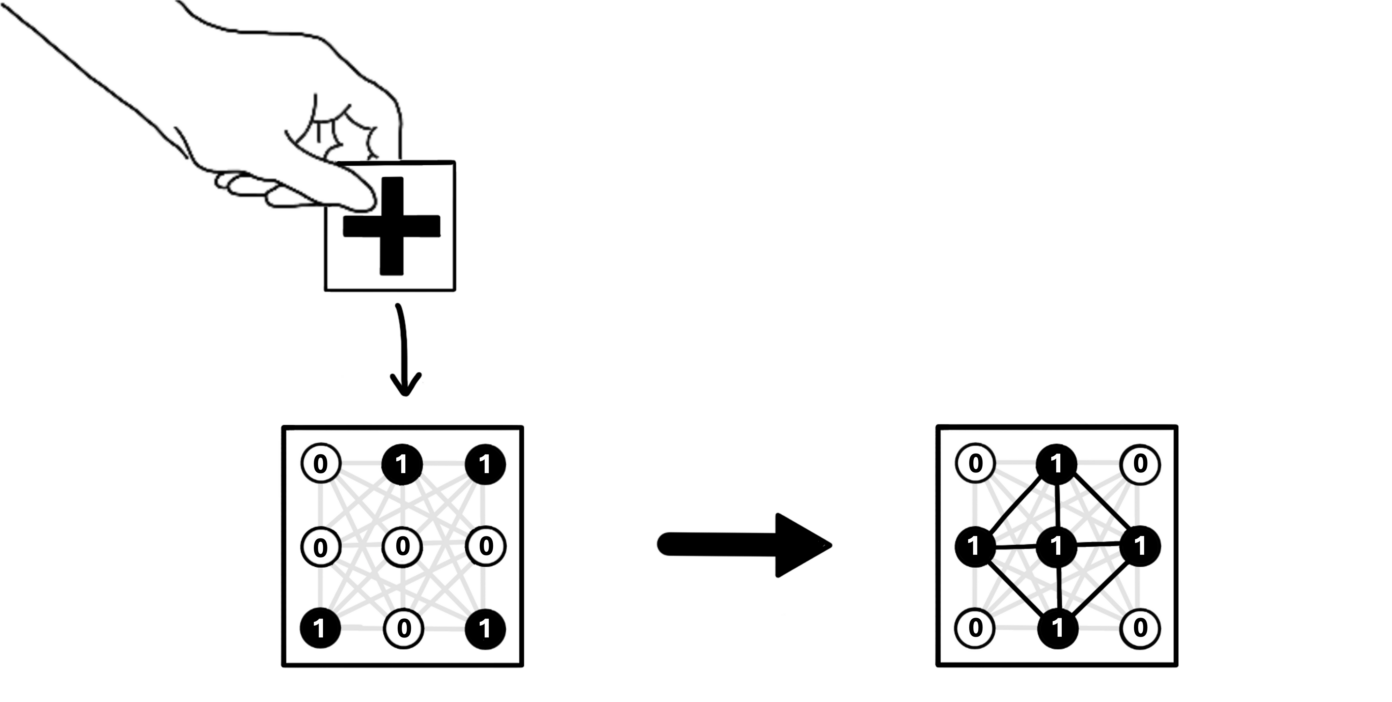
Het oorspronkelijke Hopfield-netwerk bestond uit knooppunten die de waardes 0 of 1 aan kunnen nemen en die met elkaar verbonden zijn met verbindingen van variabele sterktes. Aan iedere toestand van het netwerk (iedere verzameling van knooppuntwaardes en verbindingssterktes) wordt een bepaalde energie toegekend, die vergelijkbaar is met de energie van een magnetisch materiaal. Om het netwerk te trainen, geven we het een zwart-witafbeelding, waarbij we de witte pixels als ‘0’ invoeren, en de zwarte pixels als ‘1’. In het netwerk wordt deze informatie opgeslagen door de verbindingen tussen de knooppunten te veranderen, op zo’n manier dat de gegeven afbeelding een lage energie heeft.
Als we een andere afbeelding aan het netwerk geven, dan zal het netwerk de pixels één voor één langsgaan en voor elke pixel controleren of het netwerk een lagere energie heeft als we die pixel van kleur (in dit geval: zwart of wit) veranderen. Als dit het geval is, wordt de kleur van de pixel veranderd. Dit is vergelijkbaar met het veranderen van de elektronspin als zijn buurelektronen een tegenovergestelde spin hebben. Het proces gaat door totdat er geen verbeteringen meer mogelijk zijn. In veel gevallen zal het netwerk nu de afbeelding waarop het getraind is, gereconstrueerd hebben.
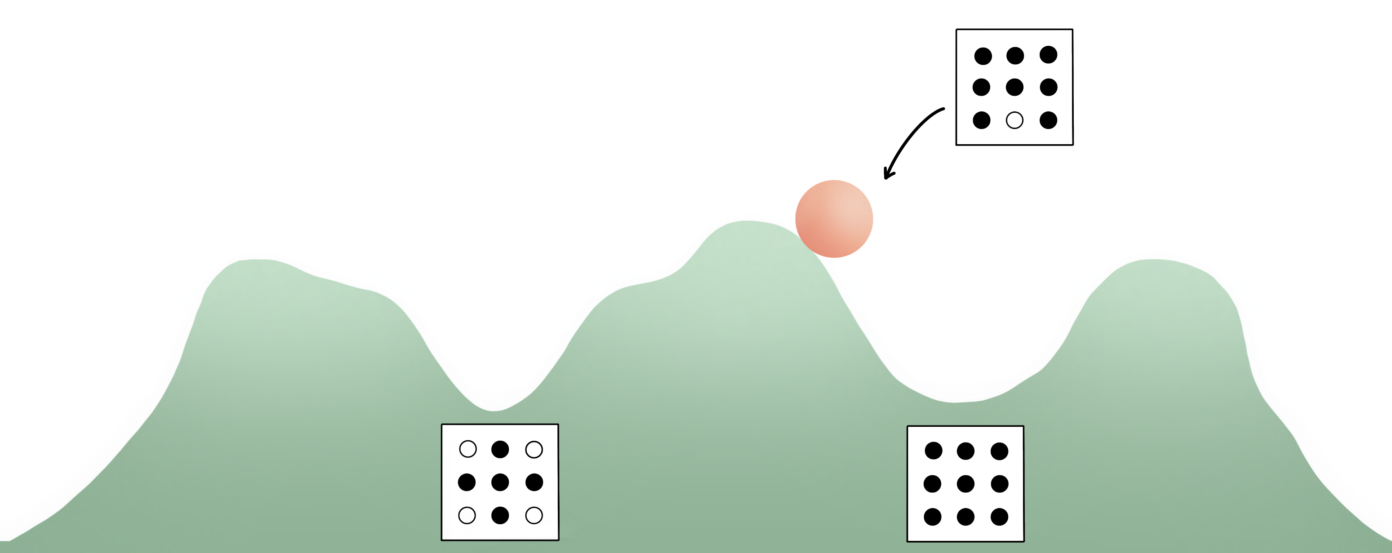
Het bijzondere aan de netwerkstructuur van Hopfield is dat deze niet alleen één patroon, maar ook een hele verzameling patronen kan opslaan. Om dit uit te leggen, vergeleek Hopfield het netwerk met een heuvelachtig landschap. Elk dal representeert een patroon dat opgeslagen is in het netwerk. Als we het netwerk een willekeurig patroon geven, is dit vergelijkbaar met het loslaten van een bal op een plek in het landschap: de bal zal naar beneden rollen totdat hij terechtkomt in een dal – de dichtstbijzijnde opgeslagen ‘herinnering’.
De Boltzmann-machine
Geoffrey Hinton en zijn collega Terrence Sejnowski bouwden voort op het werk van Hopfield door een netwerk te ontwikkelen dat niet alleen informatie kon reconstrueren, maar ook kon interpreteren. Het tweetal maakte gebruik van ideeën van Ludwig Boltzmann, een van de grondleggers van de statistische fysica. Dit gebied van de natuurkunde gebruikt kansrekening en statistiek om grote verzamelingen van ‘vrijheidsgraden’, bijvoorbeeld atomen in een gas, te beschrijven. Het idee achter het gebruik van een statistische beschrijving is dat het onmogelijk is om de bewegingen van alle moleculen in het gas te volgen, en dat we in plaats daarvan alleen de ‘gemiddelde’ eigenschappen van het gas als geheel, zoals druk en temperatuur, zien.
Boltzmann realiseerde zich dat bij één bepaalde macrosopische toestand van het gas, vastgelegd door onder andere druk en temperatuur, vele microscopische toestanden van de afzonderlijke atomen hoorden. De temperatuur komt bijvoorbeeld voort uit de gemiddelde snelheid van de atomen. Al bij een systeem van twee atomen is het duidelijk dat je de atomen veel verschillende snelheden kan geven zonder dat hun gemiddelde snelheid, en dus de temperatuur, verandert. Het ‘aantal mogelijkheden’ (zie dit artikel voor een precieze definitie van dat begrip) waarop een bepaalde toestand gerealiseerd kan worden, beïnvloedt de kans dat je het gas in die toestand aantreft: hoe meer mogelijkheden, hoe groter de kans. Boltzmann vatte dit idee samen in een wiskundige formule, die nu de naam Boltzmann-verdeling draagt.
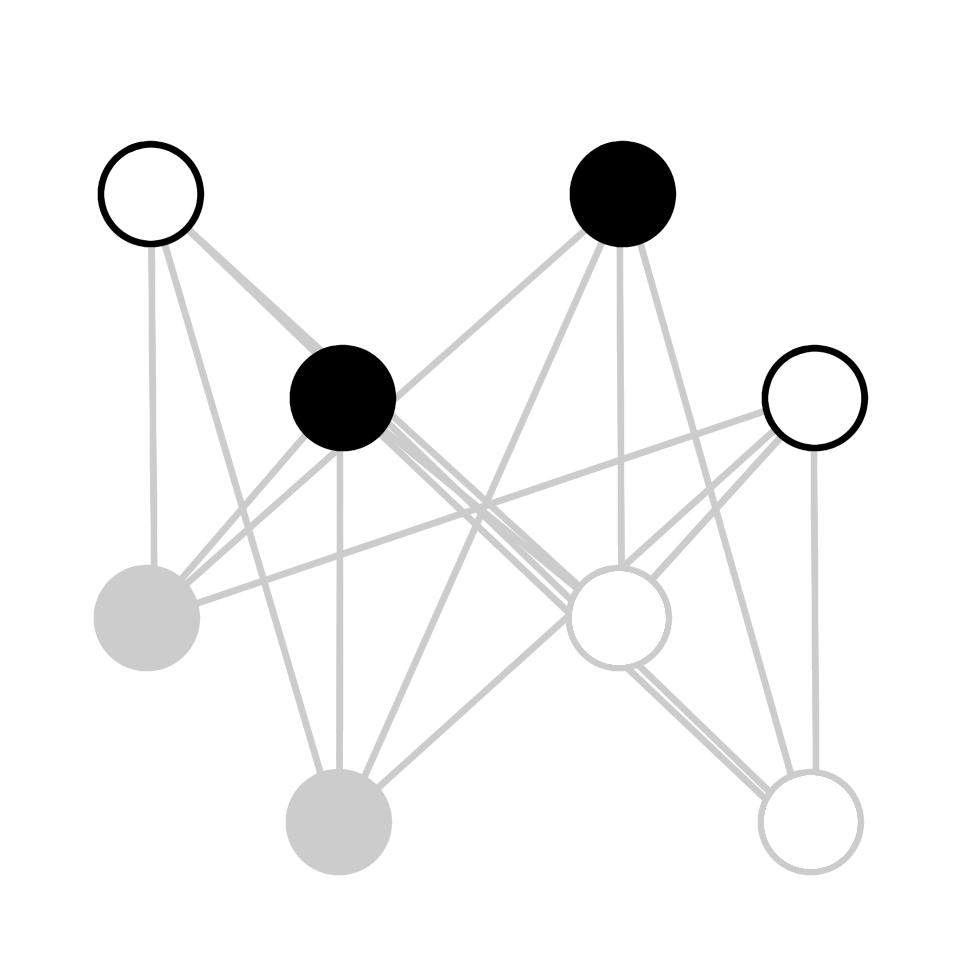
Het netwerk van Hinton en Sejnowski, dat de treffende naam Boltzmann-machine kreeg, bestaat uit twee groepen van knooppunten: de ‘zichtbare’ en de ‘verborgen’ knooppunten. Alle knooppunten dragen bij aan de werking van het netwerk, maar alleen de zichtbare knooppunten worden gebruikt om informatie uit te wisselen tussen het netwerk en de gebruiker. De verborgen knooppunten zijn toegevoegd om kansverdelingen in het netwerk te modelleren.
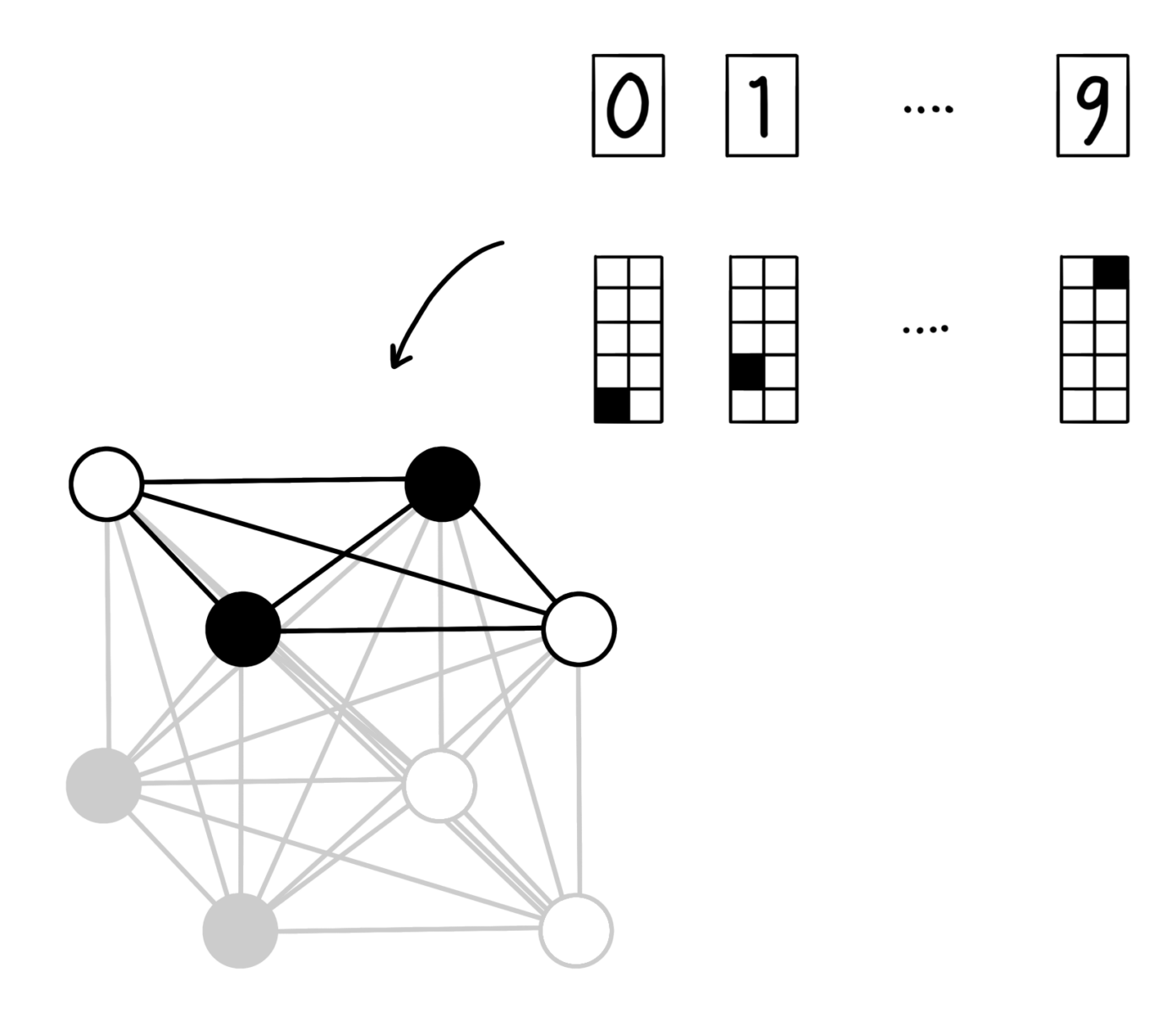
Stel bijvoorbeeld dat we het netwerk willen trainen om de getallen 0 tot en met 9 uit handschriften te herkennen. Hiervoor geven we het netwerk een verzameling van voorbeelden van zulke handgeschreven getallen, samen met een tiental pixels om te labelen welke getallen er op de afbeeldingen staan. Het leerproces komt nu neer op opslaan welke pixels vaak samen voorkomen in de trainingsdata. De verbindingssterktes in het netwerk worden aangepast, zodat vaak voorkomende combinaties een lage energie krijgen, en er dus een grote kans is dat deze combinaties tevoorschijn komen als de machine aan het werk is. De verborgen knooppunten worden hierbij gebruikt om opvallende combinaties van pixels op te slaan: een enkele streep is waarschijnlijk een 1, twee cirkels geeft een 8.
Geven we het getrainde netwerk nu een nieuwe handgeschreven 8, dan zal het op vergelijkbare manier als het Hopfield-netwerk de pixels langsgaan en veranderen, waarbij de kans groot is dat de pixel die het getal 8 labelt, aan gaat. Andersom kunnen we het netwerk ook vragen om een 8 te produceren, en zal het ons dan waarschijnlijk een afbeelding met twee verbonden cirkels geven, die meer op een 8 lijkt naarmate het netwerk beter getraind is.
De originele Boltzmann-machine was erg langzaam. Om de machine efficiënter te maken, werden de verbindingen tussen knooppunten van dezelfde soort (zichtbaar of verborgen) verwijderd, zodat er alleen nog verbindingen tussen knooppunten van verschillende soorten overbleven. Deze beperkte Boltzmann-machines worden vaak als onderdeel van een groter netwerk gebruikt. Hinton en zijn collega’s ontwikkelden bovendien een manier om een netwerk te ‘pretrainen’ met een aantal lagen van Boltzmann-machines, waarbij de verborgen knooppunten van het ene netwerk gebruikt worden als zichtbare knooppunten voor het volgende netwerk. Dit verbeterde het trainingsproces enorm.
Nobelprijsuitreiking
John Hopfield en Geoffrey Hinton krijgen op dinsdag 10 december in Stockholm de Nobelprijs voor Natuurkunde uitgereikt voor ‘fundamentele ontdekkingen en innovaties die machine learning met kunstmatige neurale netwerken mogelijk maken’. Ook de Nobelprijs voor Scheikunde gaat dit jaar naar onderzoek dat gerelateerd is aan AI. Wil je de uitreikingen van de Nobelprijzen of de bijbehorende lezingen van de prijswinnaars live meekijken, of later nog eens terugkijken, dan kan dat via deze link.