Topologie
Topologie is een tak van de wiskunde die zich bezighoudt met continue vervormingen. Iets preciezer: de centrale vraag in de topologie is welke eigenschappen van objecten niet veranderen als we het object continu (op een “vloeiende” manier) vervormen.

Afbeelding 1. Topologie.Een koffiekop en een donut zijn topologisch gezien precies hetzelfde object. Animatie: Lucas V. Barbosa.
In afbeelding 1 zien we een voorbeeld van topologie dat vaak gegeven wordt: een koffiekop en een donut hebben totaal verschillende vormen, maar zijn op continue wijze in elkaar over te vormen. De belangrijke eigenschap die deze twee voorwerpen gemeen hebben, is dat ze allebei precies één gat hebben. Een voetbal daarentegen heeft géén gaten, en is daarmee ook niet continu te vervormen tot een donut of een koffiekop.
Het aantal gaten dat een voorwerp heeft, is daarmee een voorbeeld van een topologische invariant. Het is een eigenschap die niet verandert als we een voorwerp vervormen, en daardoor kunnen voorwerpen met een verschillend aantal gaten nooit in elkaar vervormd worden.
Cruciaal hierbij is dat het aantal gaten van een voorwerp discreet is – dat wil zeggen: gegeven door een geheel getal. Er bestaat niet zoiets als een half gat, of 0,0003 gat. Dit is de wiskundige reden voor het feit dat het aantal gaten van een voorwerp niet vloeiend van 0 naar 1 kan veranderen.
Topologie in de natuur
Ook in de natuurkunde komt het begrip topologie veelvuldig voor. Kijk bijvoorbeeld eens naar afbeelding 2 hieronder. In de afbeelding zien we viermaal een vlak met een gat erin. We kunnen ons dit vlak bijvoorbeeld voorstellen als een dunne metalen plaat. In het vlak staan pijltjes getekend, die we kunnen zien als de uitbeelding van iets wat een richting heeft – denk aan de richting van magneten, de richting van een elektrisch veld, of de draaiïngsas van atomen. De pijltjes zijn zo getekend dat ze van plaats tot plaats vloeiend veranderen.

Afbeelding 2. Topologie in de natuur.De bovenste twee configuraties zijn continu in elkaar te vervormen; de onderste twee ook. De bovenste kunnen echter niet continu in de onderste vervormd worden.
Wie een tijdje naar de plaatjes staart, zal zien dat de bovenste twee configuraties continu in elkaar vervormd kunnen worden, en de onderste twee ook. Het is echter niet mogelijk om de configuraties bovenaan continu te vervormen zodat de onderste ontstaan. De onderscheidende topologische invariant is in dit geval het zogeheten windingsgetal van de pijltjes. Als we in de figuur rechtsboven “een rondje om het gat lopen”, zullen we zien dat de pijltjes weliswaar wat heen-en-weerwiebelen, maar dat ze na een heel rondje om het gat precies evenveel rechtsom gewiebeld hebben als linksom, en zo weer in hun oorspronkelijke stand zijn teruggekomen. Doen we hetzelfde echter in het onderste plaatjes, dan wiebelen de pijltjes beduidend meer rechtsom dan linksom. Na een heel rondje om het gat zijn ze precies 360 graden meer rechtsom gedraaid dan linksom, en op die manier weer in hun oorspronkelijke toestand terechtgekomen.
Er zijn ook configuraties denkbaar (teken ze zelf!) waarbij de pijltjes na een rondje om het gat 720 graden gedraaid zijn, of 1080 graden. In totaal moet de draaiing natuurlijk altijd een veelvoud van 360 graden zijn, zodat het oorspronkelijke pijltje bij terugkomst gereproduceerd wordt. Een geheel veelvoud, om precies te zijn – en daarmee hebben we weer een “onvervormbaar” discreet getal – dus: een topologische invariant – gevonden!
Minder dan 3 dimensies
In zekere zin lijkt het voorbeeld hierboven misschien wat kunstmatig. Om te beginnen is onze “natuur” (het grijze vlak met het gat erin) in dit voorbeeld tweedimensionaal, terwijl de echte wereld om ons heen driedimensionaal is. Toch zijn er in de natuurkunde allerlei systemen die bij heel goede benadering tweedimensionaal zijn. Denk aan heel dunne lagen van een materiaal die bijvoorbeeld als coating gebruikt worden, of aan het tweedimensionale grensvlak tussen twee driedimensionale materialen met heel verschillende eigenschappen. Ook ééndimensionale systemen komen in de natuur veel voor, in de vorm van draden, of in de vorm van overgangslijnen tussen twee verschillende tweedimensionale systemen.

Afbeelding 3. Een draaikolk.Een wateroppervlak is een voorbeeld van een tweedimensionaal systeem. Als er in dit oppervlak een defect is, kan er een vortex ontstaan: een draaikolk. Afbeelding: Wikipedia-gebruiker Shutinc.
Juist in zulke lagerdimensionale systemen blijkt topologie vaak een interessante rol te spelen, en het zijn juist zulke systemen die Thouless, Haldane en Kosterlitz bestudeerd hebben.
Een ander opzicht waarin ons voorbeeldsysteem nogal kunstmatig lijkt, is het feit dat er een gat in zit. Dat gat is echter van essentieel belang voor de toplogie: we moeten immers ergens een rondje omheen kunnen maken om van een windingsgetal te kunnen spreken.
Nu ogen gaten wellicht kunstmatig, maar objecten waar we omheen kunnen lopen komen in de natuur heel veel voor. Vaak is zo’n ‘object’ niet meer dan een ‘foutje’ in het systeem – bijvoorbeeld een atoom van een andere soort dan de atomen waarvan de rest van het materiaal gemaakt is, of een ‘gat’ in het wateroppervlak bij een draaikolk. Een dergelijk foutje wordt ook wel een topologisch defect genoemd. Wanneer een bepaalde eigenschap om zo’n defect heen een windingsgetal heeft, spreken we van een vortex. Het voorbeeld van de draaikolk (zie afbeelding 3) is misschien wel het bekendste voorbeeld van zo’n vortex. De pijltjes die de snelheid van het water aangeven, hebben rondom het centrum van de draaikolk een windingsgetal dat gelijk is aan 1.
Quantumvortices
Topologie en vortices komen we al tegen in de alledaagse fysica van draaikolken en wervelstormen. Het bovenstaande verhaal blijkt echter nog veel interessanter te worden als we het bekijken in de wondere wereld van de quantummechanica.
Dit is misschien een onverwacht domein om topologische fysica in te zoeken: voor iets als een draaikolk is immers een grote hoeveelheid materiaal nodig, terwijl de quantummechanica juist gaat over extreem kleine systemen, zoals individuele atomen of andere elementaire deeltjes.
Het blijkt echter dat quantummechanische effecten soms ook doordringen in veel grotere systemen. Om dit mogelijk te maken, moet zo’n systeem in extreme ‘rust’ worden gebracht, zodat allerlei grotere fluctuaties de kleine quantumeffecten niet uitdoven. Die rust wordt bereikt door een materiaal heel sterk af te koelen, vaak tot enkele graden of zelfs fracties van een graad boven het absolute temperatuurnulpunt, zo’n -273 graden Celsius. Bij dergelijke temperaturen worden quantumeigenschappen van materialen opeens op grote schaal zichtbaar, en zien we effecten zoals extreem goede stroomgeleiding (supergeleiding) of extreme vloeibaarheid van vloeistoffen (superfluïditeit).
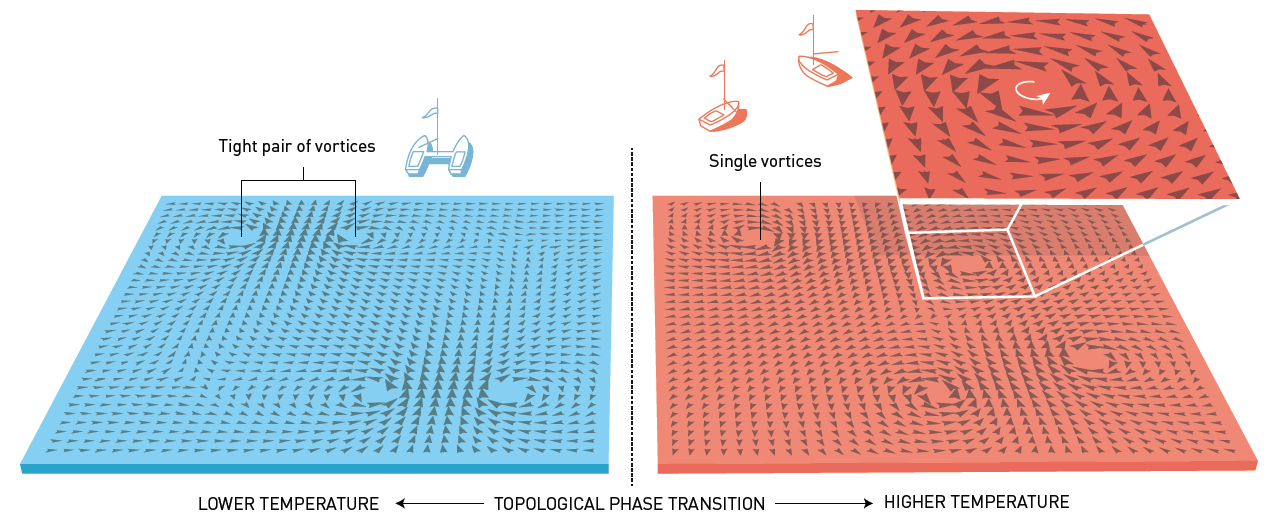
Afbeelding 4. Vortices in quantummaterie.In quantummaterie – dat wil zeggen: extreem koude materie – komen vortices vaak in paren voor. Bij hogere temperaturen kunnen de vortices los door de materie heen bewegen. Afbeelding uit de populairwetenschappelijke beschrijving bij de Nobelprijs van de Royal Swedish Academy of Sciences, gemaakt door Johan Jarnestad,
Ook vortices in materialen krijgen bij heel lage temperaturen vaak speciale eigenschappen. Zo krijgen vortices bijvoorbeeld de neiging om in tweetallen voor te komen, waarbij het windingsgetal in de ene vortex dat in de andere vortex opheft. Als we een beetje uitzoomen vanaf zo’n vortexpaar, zien we een combinatie die als geheel geen windingsgetal heeft. Het quantummateriaal blijkt een energiegunstige toestand op te zoeken waarin zo veel mogelijk van deze combinaties gevormd zijn.
Zodra we het materiaal echter opwarmen, gaat deze quantumparing op een gegeven moment verloren. Er ontstaat een materiaal waarin individuele vortices vrij rond kunnen bewegen. Een dergelijk materiaal kan totaal andere eigenschappen hebben (in termen van bijvoorbeeld stroomgeleiding, vloeibaarheid, warmtegeleiding, enzovoort) dan het oorspronkelijke gekoelde materiaal. Vergelijk dit met water, dat bij een lage temperatuur (ijs, onder de nul graden) totaal andere eigenschappen heeft dan bij een hogere temperatuur (vloeibaar water, boven de nul graden, of stoom, boven de honderd graden). Net als bij water spreken we ook in dit geval van fase-overgangen, en de verschillende toestanden worden topologische fases genoemd. Wanneer een zeldzame toestand zoals die van gepaarde vortices alleen bij zeer lage temperatuur (of andere extreme omstandigheden) voorkomt, wordt ook wel van exotische materie gesproken.
De prijzen
Thouless, Haldane en Kosterlitz wonnen hun prijzen voor het ontdekken van de theoretische mogelijkheid dat topologische fases en hun overgangen bestaan – een mogelijkheid die later ook in experimenten echt gerealiseerd bleek. Kosterlitz en Thouless beschreven als eerste het tweedimensionale voorbeeld dat we hierboven noemden; samen met Haldane beschreef Thouless (die de helft van het totale prijzenbedrag mee naar huis krijgt) ook een ééndimensionaal voorbeeld.

Afbeelding 5. De Nobelprijs.De medaille die alle Nobelprijswinnaars, naast natuurlijk een fors geldbedrag, ontvangen.
De studie naar topologische fases van materialen en de overgangen tussen die fases, begon zoals gezegd met theorie, en werd al snel ook een experimentele wetenschap. Ook de volgende stap wordt gezet: materialen waarin bijzondere fase-overgangen plaatsvinden, kennen allerlei potentiële technologische toepassingen – bijvoorbeeld voor het maken van schakelingen met bijzondere stroomgeleidingseigenschappen of het ontwikkelen van quantumcomputers. Kortom: de theorie van exotische materie leidt tot praktische toepassingen die steeds minder ‘exotisch’ worden – een ontdekking, dus, die de Nobelprijs meer dan waard is!
Meer weten?
Op het internet zijn inmiddels tal van artikelen over de Nobelprijs te vinden. Een kleine selectie:
Nederlandstalig
- Nobelprijs voor natuurkunde naar ontdekkers exotische materie, De Volkskrant, door Martijn van Calmthout.
- Nobelprijs Natuurkunde voor vreemde stroom van geknoopte elektronen, NRC, door Bruno van Wayenburg
- ‘In de zomer geeft Haldane met regelmaat workshops aan onze faculteit’, Folia, door Laura Cardona
- Nobelprijs natuurkunde voor vreemde materietoestanden, Kijk, door Jean-Paul Keulen
- Nobelprijs voor Natuurkunde voor onderzoek naar exotische toestanden van materie, New Scientist, door Dorine Schenk
- Nobelprijs Natuurkunde voor ontdekking ’topologische’ exotische materialen, De Kennis van Nu, door Arnout Jaspers
- Pfew, geen Nobelprijs voor Ronald Hanson!,Vrij Nederland, door Gerard Janssen
Engelstalig
- Populairwetenschappelijke beschrijving van de website van het Nobelcomité.
- Physics of 2D exotic matter wins Nobel, Nature, door Elizabeth Gibney en Davide Castelvecchi
- Trio snares physics Nobel for describing exotic states of matter, Science Magazine, door Adrian Cho
- 3 Who Studied Unusual States of Matter Win Nobel Prize in Physics, New York Times, door Dennis Overbye en Sewell Chan
- Physics Nobel Awarded for Breakthroughs in Exotic States of Matter, Scientific American, door Lee Billings
- Physics Nobel goes to discoverers of world of stranger things, New Scientist, door Timothy Revell
- David Thouless, Duncan Haldane and Michael Kosterlitz win 2016 Nobel Prize for Physics, Physics World, door Tushna Commissariat en Hamish Johnston
- Special over topologische materie, uit het juli-nummer van Nature.
- Webcollectie van Nature rond de Nobelprijs 2016.