
Topologie beschrijft de eigenschappen van een systeem die niet veranderen als we het systeem geleidelijk vervormen, bijvoorbeeld door het uit te rekken of te buigen. Drastische veranderingen zoals scheuren en gaten maken, kunnen de topologische eigenschappen wél veranderen. Een belangrijk voorbeeld van een materiaal met zulke robuuste eigenschappen is een topologische isolator. Dit is een materiaal dat geen elektriciteit geleidt aan de binnenkant, maar wel langs de rand. Bovendien heeft de stroom langs de rand een vaste richting. Deze oppervlaktegeleiding blijft bestaan, ongeacht kleine materiële imperfecties.
Wetenschappers van de Universiteit van Californië – San Diego vertaalden deze eigenschappen naar een dans, en leerden de dans aan scholieren van de Orange Glen High School in Escondido, Californië. De dansvloer bestaat uit een rooster van vierkanten, die plekken in het rooster van de deeltjes in het materiaal voorstellen. Op elke plek waar een elektron zich kan bevinden, staat een danser die twee vlaggetjes vasthoudt. Met deze vlaggetjes kan de danser drie dansbewegingen uitvoeren: de vlaggetjes omhoog wapperen, omlaag wapperen of stilhouden. In ieder vierkant op de vloer staan blauwe en rode lijnen, die aangeven of de dansers in die vierkanten op dezelfde manier moeten bewegen (beiden omhoog, omlaag of stil) of juist tegenovergesteld (de ene omhoog en de andere omlaag, of andersom). Verschillende dansvloeren corresponderen met verschillende natuurkundige modellen.
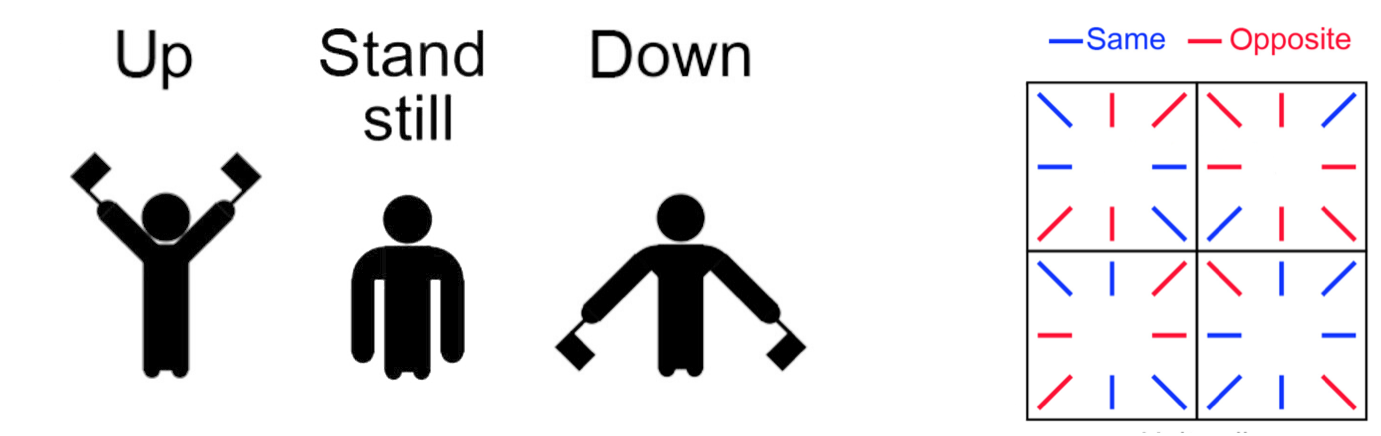
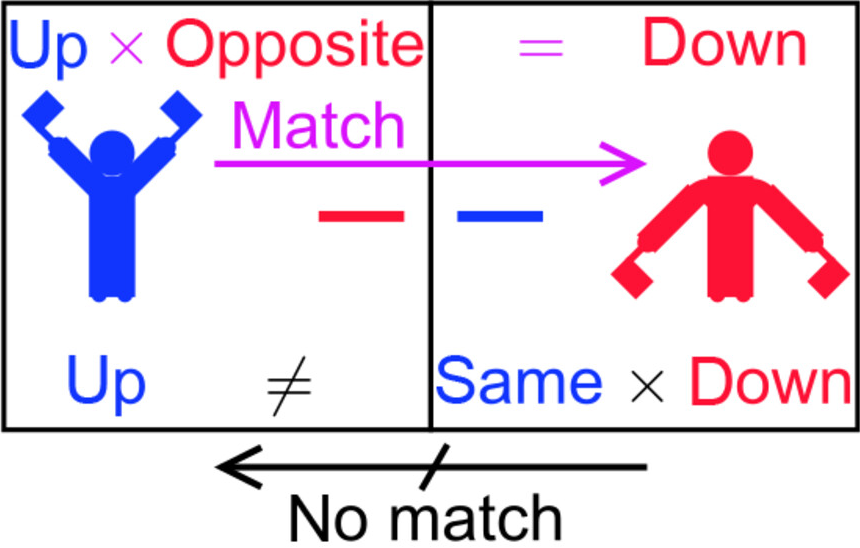
In hun onderzoek maken de wetenschappers gebruik van één vaste dansvloer1. De dans begint wanneer iemand buiten het rooster aan een van de dansers (de ‘commandant’) de opdracht geeft om de vlaggetjes naar boven of naar beneden te wapperen. Je kunt dit vergelijken met het onder spanning zetten van een topologische isolator. Vervolgens beginnen de dansers die om de commandant heen staan met hun vlaggetjes te wapperen, in dezelfde of tegenovergestelde richting, afhankelijk van de kleur van de lijn in het vierkant van de commandant in de richting van de danser. Als alle buren dansen, houdt de commandant de vlaggetjes stil. Degenen die nu met hun vlaggetjes wapperen gaan op zoek naar een ‘match’: dansen zij en (ten minste een van) hun buren in overeenstemming met de lijnen op de grond, dan stoppen ze met dansen. Voor de dansvloer uit het onderzoek is er hooguit één danser die geen matches heeft. Deze danser blijft wapperen met de vlaggetjes en wordt de nieuwe commandant, waarna het proces opnieuw begint. Op deze manier ‘loopt de stroom’ door het rooster van dansers. De dans stopt wanneer alle dansers een match hebben.
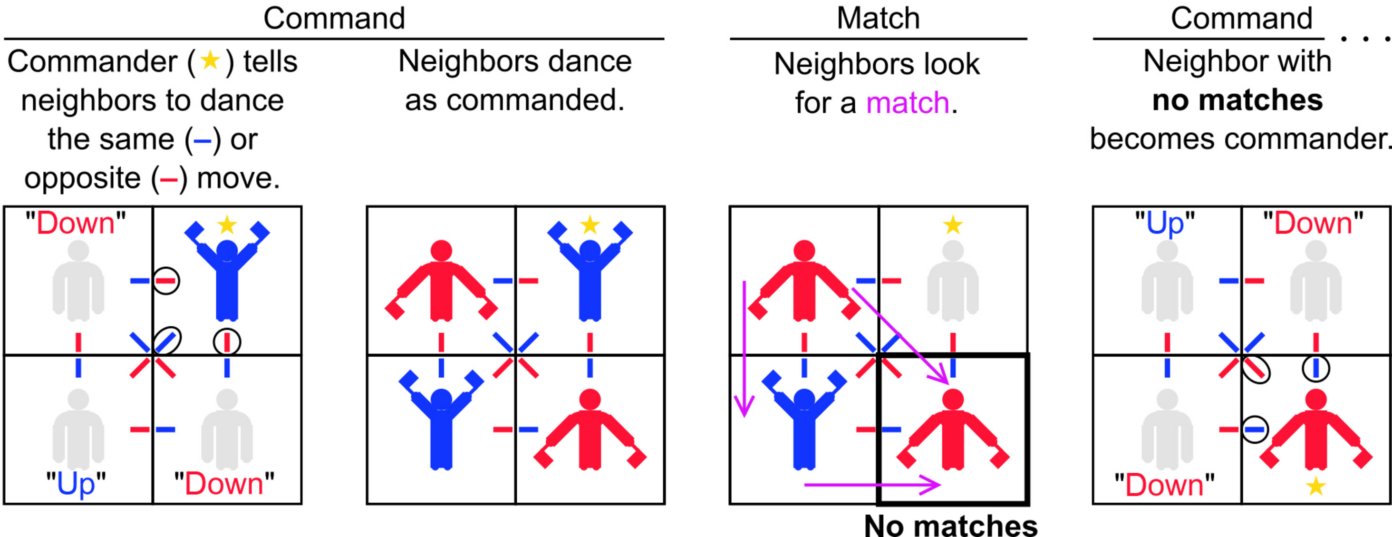
In het onderzoek worden verschillende beginsituaties van de dans bekeken. Als de eerste commandant zich aan de rand van de dansvloer bevindt, zal het commandantschap zich met de klok mee langs de rand verplaatsen. Net als met een echte topologische isolator treedt dit effect ook op als de rand niet een perfect vierkant is, maar een grillerige vorm heeft. Als de eerste commandant zich echter ergens anders op de dansvloer bevindt, zal de dans na één ronde al afgelopen zijn: niemand wordt de nieuwe commandant, en de binnenkant van de isolator geleidt in dit model dus geen stroom.
In het onderzoek ligt de focus dus op één natuurkundig model, maar de wetenschappers hopen met hun werk een blauwdruk te geven voor tastbare simulaties van verschillende topologische isolatoren.
Dit artikel is gebaseerd op de publicatie: Du, M. et al. “Chiral edge waves in a dance-based human topological insulator” Sci. Adv. 10, eadh7810 (2024). In de bijlagen bij het artikel vind je ook enkele filmpjes waarin de leerlingen de dans uitvoeren. (De afbeelding bovenaan dit artikel is een screenshot uit een van die filmpjes.)
[1] Deze dansvloer beschrijft het zogenaamde Harper-Hofstadtermodel.