Superpositie is een moeilijk voorstelbaar fenomeen. Ik zie de tafel waaraan ik nu zit, of de toetsen waarop ik typ, namelijk nooit op twee verschillende plekken tegelijkertijd. In afbeelding 1 doe ik een poging om een superpositie van het systeem “de toets Q” op mijn toetsenbord te visualiseren. De toets Q is zowel een beetje op positie X als op positie Y. Moet ik, aangezien ik zulke effecten in het dagelijkse leven niet zie, dan concluderen dat een tafel of een toets geen quantumsystemen zijn? Een intuïtief eerste antwoord op deze vraag zou “ja” kunnen zijn, maar er zijn ten minste drie bezwaren tegen deze conclusie te geven.
Allereerst impliceert een “ja” dat een tafel, die uit allemaal quantummechanische deeltjes bestaat, zelf niet quantummechanisch is. Dat zou het geval zijn als systemen vanaf een bepaalde grootte om een of andere reden plots helemaal niet meer quantum zijn. Een dergelijke overgang wordt ook wel de Heisenberg cut genoemd. Zo’n overgang voelt onnatuurlijk aan, en we kunnen er ook geen motivatie of theoretische verklaring voor geven.
Ten tweede kunnen experimentele natuurkundigen tegenwoordig van steeds grotere objecten laten zien dat ze niet alleen intern, maar ook als geheel quantumeffecten vertonen en niet zomaar klassieke systemen zijn met een exact bepaalbare positie. De Heisenberg cut, als deze bestaat, wordt door experimenten steeds verder verplaatst naar steeds grotere systemen. Deze verplaatsing suggereert dat de Heisenberg cut helemaal niet bestaat: als zelfs grote moleculen, die uit meer dan 2000 atomen bestaan, quantumeffecten vertonen, waarom zou mijn wimper dan niet ook quantumeffecten vertonen? En waarom dan niet mijn vingernagel? Of mijn hele vinger? Als de Heisenberg cut niet bestaat zijn alle systemen, ook jij en ik, quantumsystemen!
Een derde reden dat ook een groot systeem zoals mijn toetsenbord tóch een quantumsysteem kan zijn terwijl ik geen quantumeffecten observeer, is dat quantumeffecten voor grotere systemen onderdrukt kunnen worden: misschien is de toets Q wél op meerdere plekken tegelijkertijd, maar is de afstand tussen die verschillende posities zo klein dat ik de verschillen met het blote oog niet kan zien. De toets Q is dan niet op de duidelijk verschillende posities van toetsen X en Y, maar op een aantal vlak bij elkaar liggende posities tussen W en Tab. In afbeelding 2 zie je dat nog steeds wat overdreven weergegeven; ook zo’n wazige Q zien we in de praktijk natuurlijk niet. Wat we zien is afbeelding 3, waar de toets Q zich hooguit bevindt op verschillende plekken die zo dicht bij elkaar liggen dat ze niet met het blote oog van elkaar te onderscheiden zijn.
We staan dus voor een keuze. We nemen ofwel aan dat er een Heisenberg cut bestaat en dat systemen vanaf een bepaalde grootte klassiek worden. In dat geval zijn wij mensen en onze meetapparaten klassiek en staan we voor het probleem dat we geen idee hebben hoe quantumsystemen en klassieke systemen met elkaar interageren en waarom de Heisenberg cut bestaat. Als alternatief kunnen we de natuurlijkere aanname maken dat systemen die uit heel veel quantumdeeltjes bestaan nog steeds quantumsystemen zijn. Dan ontstaat er echter een ander fundamenteel probleem.
Het meetprobleem
Als alles quantum is, geldt quantummechanica op alle schalen, en is dus een universele theorie. Hier laat ik systemen die op hoge snelheden bewegen buiten beschouwing, omdat deze de theorie onnodig compliceren. Onder de aanname dat quantummechanica universeel is, vertoont de theorie echter een groot probleem, dat direct volgt uit de postulaten die de theorie vastleggen. Dit probleem is al sinds 1930, vlak na de formulering van de quantummechanica zelf, bekend als het meetprobleem omdat het zich heel duidelijk voordoet tijdens een quantummeting. Tijdens een quantummeting meet een groot meetapparaat een klein quantumsysteem en komen de quantumwereld en de door ons ervaren klassieke wereld bij elkaar. Ik zal het meetprobleem aan de hand van een voorbeeld illustreren.
Het meetapparaat
Stel dat een meetapparaat zo is ingesteld dat het kan meten of een quantumsysteem op positie X of positie Y is. Voordat een meting plaatsvindt is het meetapparaat in de neutrale toestand:
Na het meten is het meetapparaat in de toestand
afhankelijk van de positie van het gemeten quantumsysteem. Merk op dat we de toestand
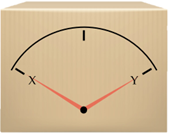
een superpositie van de twee, nooit observeren: het meetapparaat heeft maar één pijl en die zien we nooit op twee verschillende plaatsen tegelijkertijd.
Het gemeten systeem
Stel nu dat we de locatie van een enkel watermolecuul gaan meten. Zo’n molecuul kunnen we schematisch zo weergeven:
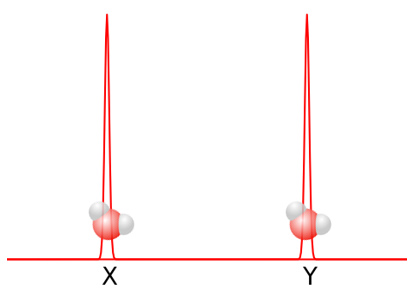
Een ‘klassiek’ watermolecuul zou zich op een vaste positie bevinden – in ons voorbeeld ofwel op positie X, ofwel op positie Y:
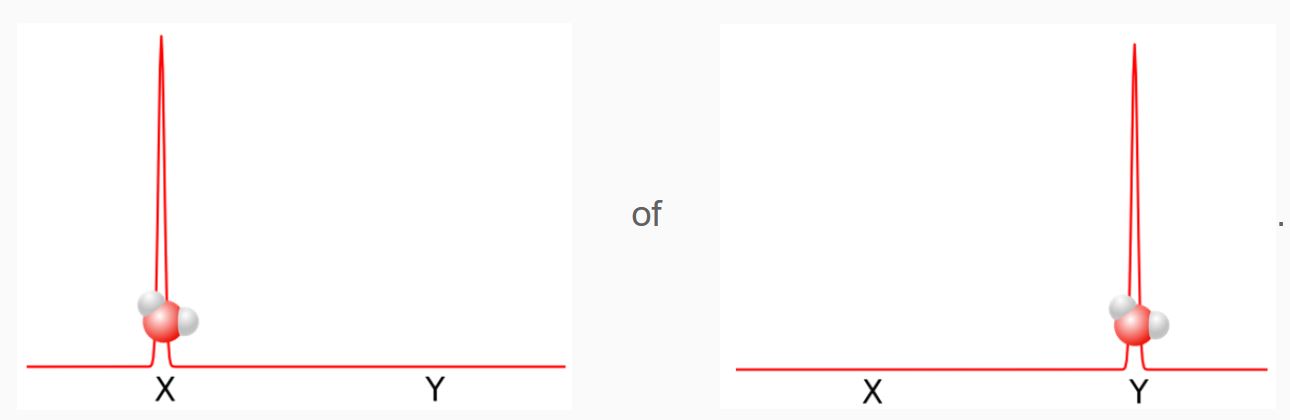
De gepiekte grafiekjes op de achtergrond (waarvoor de technische term de golffunctie is) geven weer dat het molecuul in deze toestanden echt maar op één plaats is. Quantummechanisch gezien kan het molecuul echter ook op beide posities tegelijk zijn:
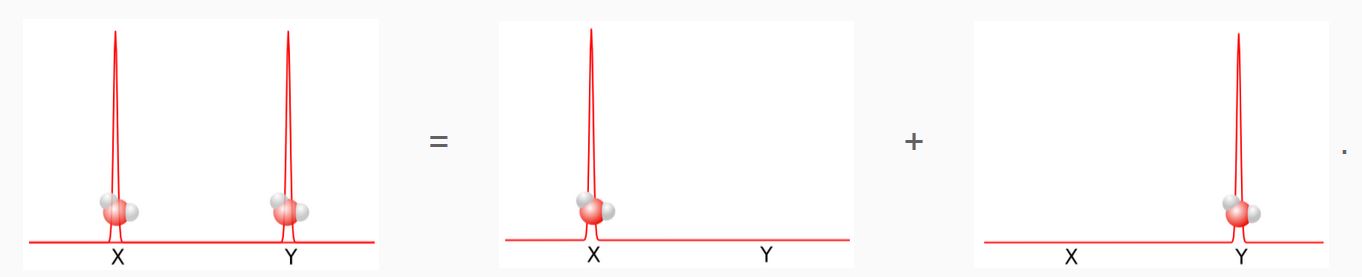
In de bovenstaande afbeelding bevindt het watermolecuul zich dus in een superpositie van twee verschillende posities, wiskundig1 aangegeven met de “+”.
De meting
De tijdsevolutie van een systeem beschrijft de verandering van het systeem terwijl de tijd verstrijkt. Voor quantumsystemen wordt de tijdsevolutie gegeven door de zogeheten Schrödingervergelijking. De wiskundige details van die vergelijking doen hier niet ter zake; in plaats daarvan zal ik een schematische weergave geven van de evolutie van het systeem
“meetapparaat” & “waterstofmolecuul”
wanneer we een quantummeting doen. Hierbij zal ik het “&”-teken gebruiken om het tegelijkertijd samenzijn van twee quantumsystemen weer te geven.2
We beginnen met het meetapparaat in neutrale toestand en het watermolecuul in een superpositie, oftewel:
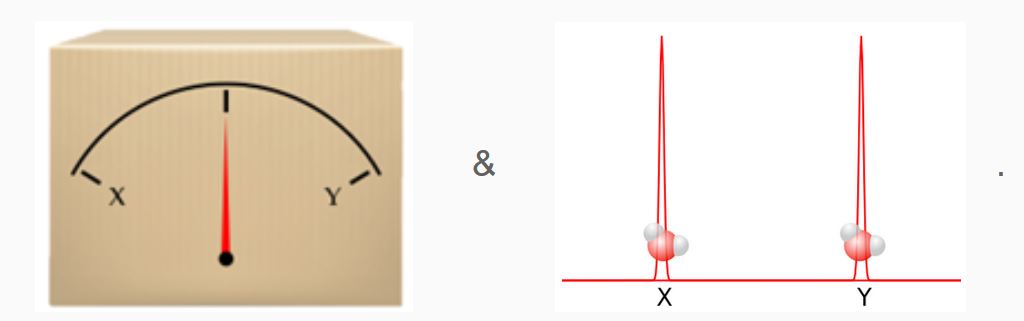Bovenstaande toestand is – per definitie van de superpositie – gelijk aan de toestand
In de wiskunde van de quantummechanica kunnen we de haakjes uitwerken; door dat te doen kunnen we deze toestand dus ook schrijven als
Aangenomen dat ons meetapparaat een goed meetapparaat is, zal een interactie tussen het meetapparaat en het waterstofmolecuul ervoor zorgen dat het meetapparaat de positie van het waterstofmolecuul aangeeft. Evolutie volgens de Schrödingervergelijking vertelt ons dan dat bovenstaande toestand na de interactie tussen molecuul en meetapparaat de volgende toestand wordt:
Maar nu is er een erg onnatuurlijke situatie ontstaan: het quantumsysteem bestaande uit “meetapparaat” & “watermolecuul” bevindt zich als geheel in een superpositie: er geldt dat het meetapparaat X aangeeft en het watermolecuul op X is én er geldt dat het meetapparaat Y aangeeft en het watermolecuul op Y is, op hetzelfde moment. Oftewel, als je het meetapparaat nu weer als los systeem beschouwt is het in de superpositie
terechtgekomen, waarover ik eerder opmerkte dat we deze nooit observeren! Wat is er aan de hand? Het antwoord is “eenvoudigweg” dat we tegen het meetprobleem zijn aangelopen: door metingen te beschrijven via tijdsevolutie met de Schrödingervergelijking ontstaan er onvermijdelijk vreemde superposities die we in het dagelijks leven niet zien. Om het verhaal overzichtelijk te houden heb ik hierboven niet alle wiskundige details genoemd, maar ook mét deze details volgt het meetprobleem uit:
- de rekenregels van de quantummechanica – dat wil zeggen: rekenregels over hoe je twee quantumsystemen samen beschrijft, hoe je superposities beschrijft, en hoe een quantumsysteem in de loop van de tijd evolueert,
- én de aanname dat quantumtheorie universeel is, dus op alle schalen geldt.
Oplossingen voor het meetprobleem
We staat voor een groot probleem: onze quantummechanische theorie kan niet verklaren waarom we geen vreemde superposities van grote systemen, zoals toetsen, tafels en mensen zien. Sterker nog: de theorie voorspelt dat we ze wel zien! En dat terwijl de theorie voor kleine systemen juist ontzettend precieze voorspellingen doet en vele problemen oplost. Hebben we iets over het hoofd gezien, of is onze theorie incompleet? Over het antwoord op deze vraag zijn de meningen in de wetenschappelijke gemeenschap al bijna een eeuw lang verdeeld.
Interpretaties van de quantummechanica
Sommige wetenschappers zeggen dat de quantummechanica anders geïnterpreteerd moet worden dan ik zojuist impliciet heb gedaan. Door de theorie te herinterpreteren kan het meetprobleem soms voorkomen en ogenschijnlijk opgelost worden. Twee bekende voorbeelden van herinterpretaties van de quantumtheorie zijn de statistische interpretatie en de vele-werelden (many worlds) interpretatie.
Kortgezegd zegt de statistische interpretatie dat de superposities waar ik eerder over sprak, dus bijvoorbeeld de superpositie van het watermolecuul op twee locaties:
niet het quantumsysteem zelf weergeven, maar enkel de mogelijkheden waarin het systeem zich kan bevinden. In dat geval is de superpositie
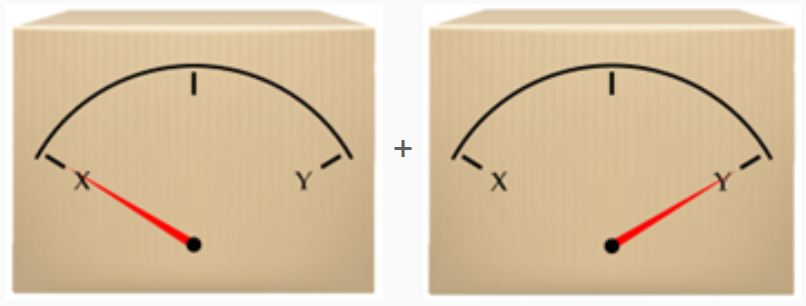
van het meetapparaat in twee verschillende posities ook niet vreemd. Inderdaad: het meetapparaat kan naar links wijzen en het kan naar rechts wijzen. Het lastige aan de statistische interpretatie is dat de interpretatie niet uitlegt hoe gedurende onze meting van de positie van het watermolecuul de ene keer de toestand
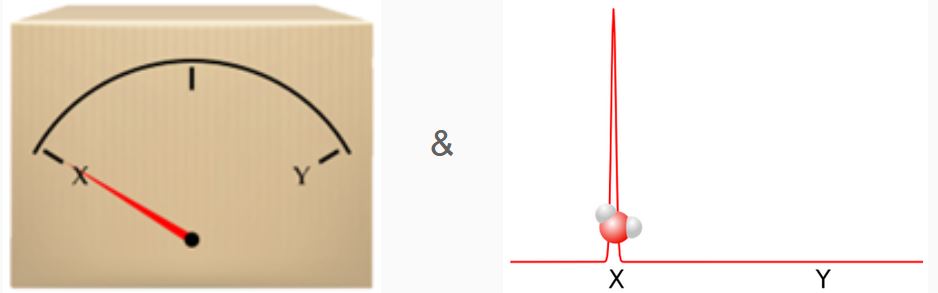
en de andere keer de toestand
ontstaat. Het meetprobleem lijkt door de statistische interpretatie dus nog niet helemaal opgelost.
De velen-wereldeninterpretatie zegt iets anders interessants, namelijk dat in een superpositie van een groot systeem, zoals het systeem “meetapparaat” & “watermolecuul” na interactie
de twee verschillende toestanden twee verschillende werelden beschrijven. Dit wil zeggen dat de wereld, als ik de positie van het watermolecuul meet, opsplitst in twee werelden. De eerste wereld is in de toestand
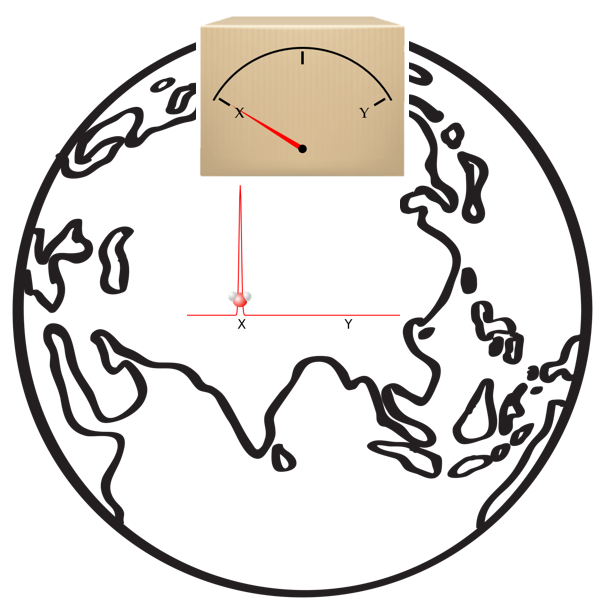
en de tweede wereld is in de toestand
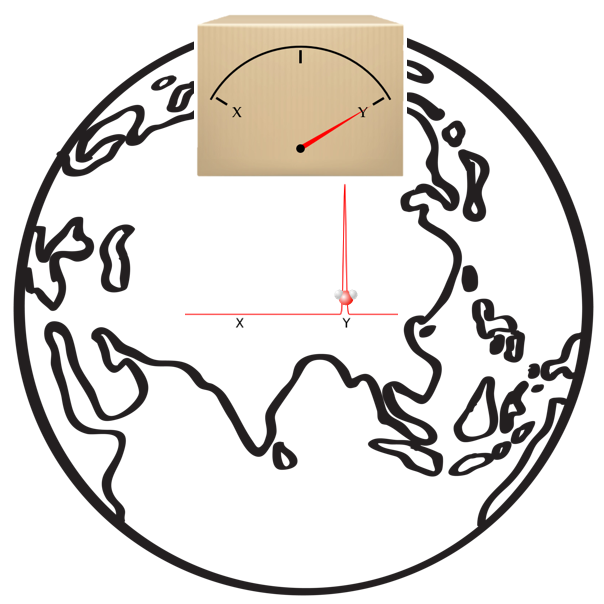
Ik heb de aarde bij ons quantumsysteem weergegeven om aan te geven dat het echt gaat om een splitsing van de hele wereld – eigenlijk zelfs van het hele universum: één universum waarin positie X wordt gemeten, en één universum waarin positie Y wordt gemeten. Er zijn vanaf de meting dus ook twee versies van mij: één die positie X observeert, en één die positie Y observeert. Omdat de twee toestanden in de superpositie verschillende werelden representeren, komt één van die versies van mij, die in één van de twee werelden zit, de vreemde superpositie
nooit tegen en is er dus geen meetprobleem. De vele-wereldeninterpretatie is een conceptueel interessante quantuminterpretatie die in populariteit groeit. Een van de nadelen van de interpretatie is dat de kansen waarmee een zekere meting gedaan wordt moeilijk te interpreteren zijn. In de vele-wereldeninterpretatie splitst de wereld bij elke meting, maar wat betekent het om met meer kans in de ene dan in de andere wereld terecht te komen als beide werelden werkelijk zijn?
Een aangepaste theorie
Voor alle quantuminterpretaties geldt dat ze de quantumtheorie niet veranderen. De voorspellingen die de interpretaties doen verschillen niet van elkaar of van de voorspellingen van de standaardinterpretatie van de quantummechanica. Een voorkeur voor de ene of de andere interpretatie is daarom gebaseerd op persoonlijke of filosofische redenen. Bovendien hebben de verschillende interpretaties elk nog hun eigen gebreken in het oplossen van het meetprobleem. We hebben bijvoorbeeld gezien dat in de statistische interpretatie niet uitgelegd kan worden hoe een toestand bij een enkele meting verandert, en dat in de vele-wereldeninterpretatie kansen moeilijk te interpreteren zijn. Naast al die interpretaties is er echter nog een alternatief mogelijk, dat bovendien voorspellingen doet die meetbaar verschillen van standaard quantumtheorie. Het is idee is als volgt.
Zou het kunnen dat de Schrödingervergelijking, die de evolutie van elk quantumsysteem beschrijft, slechts een benadering van de quantumwerkelijkheid is? Misschien is een kleine aanpassing van de vergelijking wel in staat om het meetprobleem op te lossen! Zogeheten objective collapse theories (in het Nederlands: objectieve ineenstortingstheorieën, maar deze benaming wordt nergens gebruikt) laten zien dat het inderdaad mogelijk is om quantummeting te modelleren door de Schrödingervergelijking aan te passen, zonder de succesvolle voorspellingen die de standaard quantummechanica doet te verliezen. Zo bieden objective collapse-theorieën een mogelijke oplossing voor het meetprobleem. Door een kleine verstoring aan de Schrödingervergelijking toe te voegen kan een quantummeting dan dynamisch worden beschreven, wat wil zeggen dat we de evolutie van de toestand
naar bijvoorbeeld de toestand
met onze vergelijking beschrijven. Aangezien we de ene keer het watermolecuul op positie X en de andere keer het watermolecuul op positie Y vinden, zal de verstoring van de Schrödingervergelijking stochastisch moeten zijn. Dit wil zeggen dat de verstoring van een variabele afhangt die voor elke afzonderlijke meting een andere waarde aanneemt.
Maar hoe ziet deze verstoring er dan uit? Hoe zorgen we ervoor dat de aangepaste vergelijking niet té veel afwijkt van standaard quantummechanica? Om deze vragen te beantwoorden moeten theoretische en experimentele natuurkunde nauw samenwerken. Aan de theoretische kant is het de kunst om een vergelijking te geven die fysisch gemotiveerd is en overeenkomt met de experimenten: vreemde superposities – zoals die van ons meetapparaat, met één pijltje op twee posities – moeten instabiel zijn onder de verstoring en vrijwel meteen naar een van de bekende klassieke toestanden evolueren. Deze evolutie gaat zo snel dat we hem niet kunnen observeren. De tijdsevolutie van kleine, onbetwiste quantumsystemen zoals het watermolecuul blijft echter vrijwel onverstoord en zal zich als een quantumsysteem blijven gedragen. Op deze manier komt de theorie overeen met de huidige experimenten.
Voor iets minder grote systemen dan het meetapparaat – systemen die in grootte tussen de kleine quantumsystemen en de grote, ogenschijnlijk klassieke systemen in zitten – zal de evolutie van een superpositie naar een ‘klassieke toestand’ echter wél plaatsvinden en een bepaalde meetbare tijd duren. Het is absoluut niet makkelijk om zulke betrekkelijk grote systemen in een superpositie te brengen, maar in principe kunnen we testen of quantumsystemen evolueren volgens de Schrödingervergelijking of volgens een aangepaste Schrödingervergelijking. Pogingen tot zulke testen worden al gedaan in onder andere Leiden, via een reeks van indrukwekkende experimenten die beogen steeds grotere systemen in een superpositie te brengen. Deze experimenten zijn nog volop in ontwikkeling en zullen ons op den duur hopelijk nieuwe inzichten geven.
Er is nog veel meer over motivaties voor en bezwaren tegen objective collapse-theorieën en verschillende quantuminterpretaties te vertellen, maar dat is iets voor een volgend artikel. Voor nu heb ik hopelijk laten zien dat een groot theoretisch probleem – het meetprobleem van de quantummechanica – vele mogelijke oplossingen van zowel filosofische als theoretische aard heeft, maar dat de juiste oplossing uiteindelijk toch door de experimenten, onze relatie met de werkelijkheid, bepaald wordt!
[1] Voor de liefhebbers: we laten hier numerieke factoren die aangeven dat het molecuul ‘half’ in de ene en ‘half’ in de andere toestand is achterwege. In nette wiskundige termen: we werken met niet-genormeerde golffuncties.
[2] Normaal wordt hiervoor het symbool “\( $\otimes$ \)” gebruikt, om een wiskundige operatie aan te geven die het tensorproduct heet.