Leven in een universum met maar één ruimtelijke dimensie klinkt niet als een pretje. Het blijkt echter dat de natuurkunde in deze vereenvoudigde modellen erg interessant is en ons veel kan leren over de natuurkunde in ons eigen heelal. Zo is in twee dimensies (we tellen de tijd meestal ook mee) een quantumbeschrijving van zwaartekracht binnen handbereik door gebruik te maken van toevalsoppervlakken en toevalsmatrices. In onze eigen vier dimensies is zoiets nog altijd niet goed gelukt! In dit vervolgartikel op ons artikel ‘toevalsmatrices en zware atoomkernen’ zullen we eerst uitleggen wat men precies bedoelt met tweedimensionale zwaartekracht en het begrip toevalsoppervlak, en vervolgens hoe toevalsmatrices kunnen worden ingezet om deze oppervlakken te modelleren.
Zwaartekracht in twee dimensies
De statistiek van toevalsoppervlakken is al sinds het begin van de jaren 80 goed bestudeerd. De originele motivatie voor het bekijken van deze wiskundige objecten kwam vanuit de natuurkunde: uit de zoektocht naar een quantumbeschrijving van zwaartekracht. Zoals al in eerdere artikelen op deze website is beschreven, is het enorm lastig om Einsteins algemene relativiteitstheorie – die de zwaartekracht tussen objecten in ons heelal beschrijft – en de quantumfysica – waarmee we natuurkunde op hele kleine schaal beschrijven – met elkaar te verenigen. Hoewel veel natuurkundigen hier hun hoofd over hebben gebroken, is dit probleem nog steeds verre van opgelost. Een manier om toch vooruitgang te boeken in zo’n situatie is om een eenvoudiger vraagstuk te bekijken dat genoeg overeenkomsten heeft met het probleem dat we willen oplossen. Eén zo’n vereenvoudiging is om zwaartekracht niet in onze gebruikelijke drie ruimtelijke dimensies te bekijken, maar in een model met minder dimensies. Dit vereist wat voorstellingsvermogen. Zo zou je je wellicht kunnen voorstellen dat we in een universum leven met maar één ruimtelijke dimensie: in plaats van de drie richtingen waarin we ons normaal gesproken kunnen bewegen (boven/onder, links/rechts, voor/achter), kunnen we ons in dit nieuwe universum enkel in één richting heen en weer bewegen, bijvoorbeeld naar links en naar rechts. Hieronder zie je een afbeelding waarin duidelijk is hoe de twee situaties van elkaar verschillen. De bewoners van het eendimensionale universum leven op een lijn. De hoop is nu dat de natuurkunde in dit vereenvoudigde universum ons iets kan leren over de natuurkunde in ons eigen heelal.
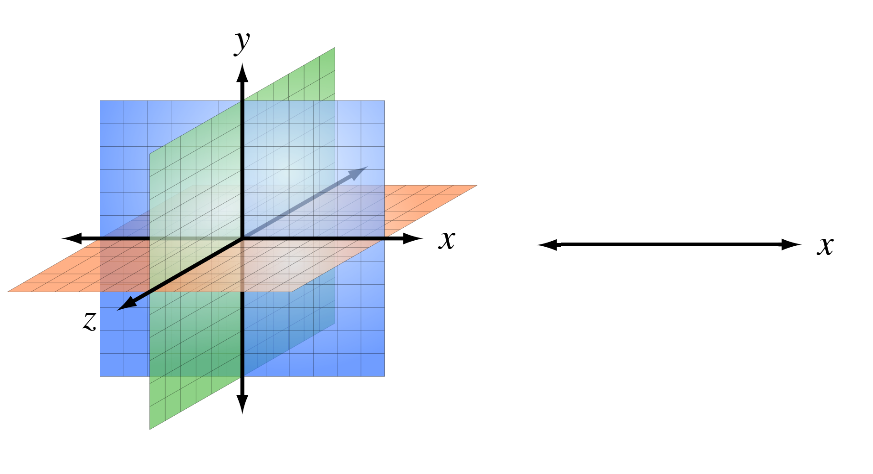
Afbeelding 1. Dimensies.Links: Een universum met drie ruimtelijke dimensies aangegeven met x,y en z. (Afbeelding: Sakurambo~commonswiki.) Rechts: een universum met één ruimtelijke dimensie aangegeven met x.
In de bovenstaande plaatjes komt de tijd niet voor. Binnen de natuurkunde is het echter gebruikelijk om ruimte en tijd op gelijk voet te behandelen en daarom ook tijd als een extra dimensie toe te voegen. De ruimtetijd van ons eigen universum is daarmee vierdimensionaal en het vereenvoudigde model heeft een ruimtetijd met twee dimensies. Bij de vier dimensies van onze eigen ruimtetijd is het lastig om je nog iets voor te stellen, maar een ruimtetijd van twee dimensies kun je gewoon tekenen als een vlak met één ruimte- en één tijddimensie.
Laten we nu bekijken hoe zwaartekracht zich gedraagt in dit vereenvoudigde tweedimensionale model. Om te beginnen staan we toe dat de ruimtetijd een meer algemene vorm kan aannemen – dus niet per se een plat vlak zoals hierboven beschreven. In deze wiskundige veralgemenisering kan de ruimtetijd de vorm hebben van ieder oppervlak in twee dimensies, bijvoorbeeld een boloppervlak, of een donutoppervlak (een torus), om maar iets exotisch te noemen.

Afbeelding 2. Een torus.Een mogelijke vorm van een tweedimensionale ruimtetijd: de torus. Afbeelding: Oleg Alexandrov.
Wat betekent het om zwaartekracht te hebben op dit oppervlak? Eén manier om over zwaartekracht na te denken is in termen van de meetkunde van het oppervlak. Om precies te zijn: de natuurkundige formules die beschrijven hoe objecten in een zwaartekrachtsveld bewegen, kunnen worden afgeleid uit de manier waarop afstanden in ruimtetijd worden gemeten en hoe vlak of krom de ruimtetijd op een bepaalde plek is. Als deze uitleg niet meteen duidelijk is, hoef je je niet druk te maken: dit is in feite een samenvatting van Einsteins algemene relativiteitstheorie in één zin! Voor nu is het belangrijk om te onthouden dat het bestuderen van zwaartekracht gelijk staat aan het bestuderen van de meetkunde van de ruimtetijd. Het abstracte wiskundige object dat alle informatie over deze meetkunde en de afstanden op een oppervlak bevat, is de zogenaamde metriek. Twee verschillende metrieken op hetzelfde oppervlak kun je interpreteren als twee verschillende zwaartekrachtsvelden op een ruimtetijd met dezelfde globale vorm. Gegeven een bepaalde metriek kunnen we in theorie berekenen hoe bepaalde objecten gaan bewegen onder invloed van dit zwaartekrachtsveld.
Quantumzwaartekracht en toevalsoppervlakken
Tot dusver hebben we het woord quantumfysica nog niet genoemd. De beschrijving van zwaartekracht in termen van meetkunde is volledig ‘klassiek’: daarmee bedoelen we dat die beschrijving erg goed blijkt te werken voor objecten die groot genoeg zijn. De grote vraag is nu of het verband tussen zwaartekracht en meetkunde nog steeds geldt op de hele kleine schalen waar quantumfysica een rol speelt. Het probleem van quantumzwaartekracht bestaat eruit om de bovenstaande meetkundige beschrijving van zwaartekracht te verenigen met de quantumtheorie van de allerkleinste deeltjes. Dat is niet eenvoudig, maar het blijkt dat er voor tweedimensionale zwaartekracht een aanpak is die heel dicht in de buurt komt van een oplossing.
Om deze aanpak te begrijpen is het noodzakelijk om één belangrijk aspect van de quantumfysica verder toe te lichten: het idee van Richard Feynman dat je in een quantumberekening alle mogelijke ‘paden’ mee moet rekenen. Een manier om het verschil tussen de klassieke- en de quantumwereld te formuleren is namelijk als volgt: waar een klassiek deeltje zich via een vast pad van punt A naar punt B beweegt (een kanonskogel bijvoorbeeld altijd in een paraboolbaan), bewandelt een quantumdeeltje in feite alle mogelijke paden van A naar B elk met een bepaalde kans. Feynman bedacht hoe je al deze mogelijkheden in één berekening kunt meenemen – zie voor meer daarover bijvoorbeeld dit of dit artikel. In de context van zwaartekracht komt het bestuderen van alle ‘paden’ overeen met de uitspraak dat alle mogelijke metrieken – dat wil zeggen: alle mogelijke zwaartekrachtsvelden – op het oppervlak kunnen voorkomen, elk met een bepaalde kans. De metriek en de vorm van het oppervlak hangen in dit quantummodel dus van het toeval af, en worden daarom ook wel toevalsoppervlakken genoemd. Om iets te kunnen zeggen over quantumzwaartekracht moeten we daarom een manier vinden om de informatie over al deze mogelijke toevalsoppervlakken op te sommen.
Dit is precies waar de toevalsmatrices van pas komen. Zoals in het vorige artikel al duidelijk werd, zijn matrices vaak een heel handige manier om informatie over een natuurkundig probleem op te slaan. We hebben daar gezien hoe de energieniveaus van zware atoomkernen kunnen worden gemodelleerd via een matrix die van het toeval afhangt. Nu zullen we zien dat deze toevalsmatrices ook een mooie manier geven om toevalsoppervlakken te beschrijven. De cruciale stap die deze identificatie mogelijk maakt is een laatste vereenvoudiging van het probleem.
Hoe betegel je een oppervlak?
Zoals al eerder benadrukt is, kan de metriek op een gegeven toevalsoppervlak een erg gecompliceerd object zijn: de metriek bevat immers informatie over afstanden tussen alle punten op het oppervlak. Een veel gebruikte manier om toch iets te zeggen over de verschillende mogelijkheden is door de metriek te benaderen met een betegeling van het oppervlak. Wat bedoelen we precies met een betegeling? Dit kunnen we het beste uitleggen met een voorbeeld:
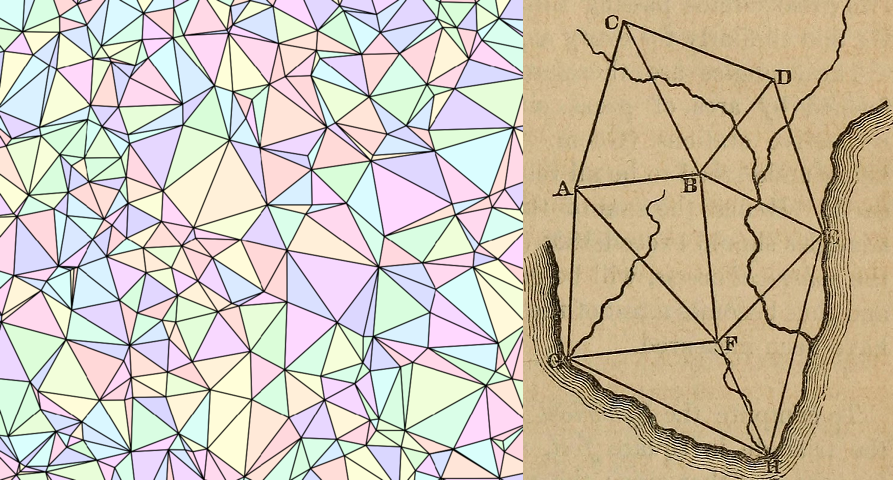
Afbeelding 3. Betegelingen.Links: een voorbeeld van een betegeling van het vlak. (Afbeelding: Adam Becker, University of Michigan.) Rechts: afstandsbepaling op een landkaart. (Afbeelding uit “Elements of trigonometry“.)
In de bovenstaande afbeelding (links) zien we een betegeling van het vlak met tegels in de vorm van een driehoek. In een dergelijke betegeling heeft iedere tegelrand een vaste lengte en op deze manier geeft dit ons een afstandsbegrip tussen verschillende tegelhoeken. Dit is te vergelijken met een landkaart waarop verschillende steden – zoals in de afbeelding (rechts) hierboven – zijn verbonden via een rechte weg. Door een lengte toe te kennen aan de zijdes van de driehoeken kunnen we de reisafstand tussen verschillende steden bepalen. Het mooie is dat je hiermee ook kromming kunt weergeven: als de landkaart rechts een groot deel van de aardbol omvat, kun je uit de afstanden tussen de steden bijvoorbeeld afleiden dat die niet op een plat vlak maar op een bol liggen! Een betegeling lijkt daarmee erg op het concept van metriek – de betegeling geeft ons een afstand tussen de verschillende hoekpunten van de betegeling. Er is echter een belangrijk verschil! Waar de betegeling alleen een manier geeft om afstanden te meten tussen de verschillende hoekpunten van de tegels, bevat een metriek de informatie over de afstanden tussen alle punten op het oppervlak. Daarom vormt een betegeling alleen een benadering van een metriek. Door meer en meer (steeds kleinere) tegels te blijven toevoegen kun je je voorstellen dat je een steeds betere en betere benadering krijgt van een metriek op het oppervlak.

Afbeelding 4. Een betegeling van een torus.Een betegeling van de ruimtetijd uit afbeelding 2. Afbeelding: Fashionslide.
De statistiek van toevalsmatrices
Om quantumzwaartekracht te beschrijven laten we de verschillende betegelingen van het toeval afhangen: met iedere betegeling associëren we een bepaalde kans. De reden dat zwaartekracht in twee dimensies bijzonder is, is dat we de informatie van zo’n betegeling efficiënt in termen van een toevalsmatrix kunnen schrijven. Dat is niet heel onlogisch: voor een betegeling in twee dimensies hoef je alleen maar een lijstje punten op te schrijven, en vervolgens tussen elke twee punten de afstand te geven. Die informatie past heel mooi in een tabel – de hoeveelheid informatie die je moet geven is dus precies de hoeveelheid informatie die in een matrix past! Het verband tussen metrieken en toevalsmatrices geeft ons een manier om daadwerkelijk berekeningen te doen en dingen te modelleren. In iedere betegeling kunnen we een netwerk tekenen door in het midden van iedere driehoek een punt te zetten en de middelpunten van aangrenzende driehoeken met elkaar te verbinden. In de afbeelding hieronder is zo’n netwerk van punten en lijnen weergeven. Zoals je kunt zien heeft dit netwerk punten waaruit steeds drie lijnen ontspingen.
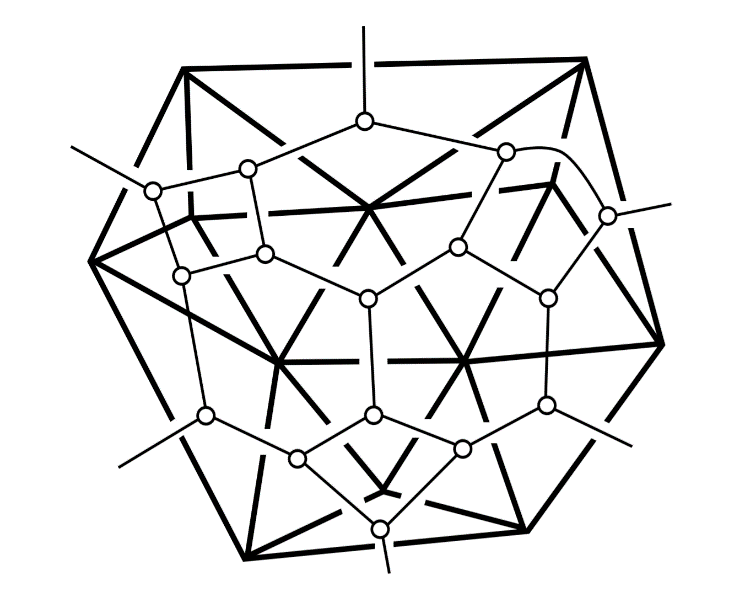
Afbeelding 5. Van betegeling naar netwerk.Een voorbeeld van een netwerk behorende bij een betegeling. (Afbeelding uit lecture 10 van de notes van Bram Petri.)
Er blijkt een manier te zijn zulke netwerken behorende bij een betegeling in termen van toevalsmatrices te schrijven. Het precieze voorschrift om dit te doen is een beetje technisch en zullen we hier niet uitgebreid uitleggen, maar wie in meer detail wil weten hoe dit zit kan dit artikel over Feynmandiagrammen nog eens lezen. Daar wordt uitgelegd hoe Richard Feynman (inderdaad: dezelfde natuurkundige die we eerder noemden) een manier vond om een quantumtheorie te beschrijven aan de hand van betrekkelijk eenvoudige diagrammen: Feynmandiagrammen. Het mooie is nu: als we een geschikte quantumtheorie van toevalsmatrices opstellen, zijn deze Feynmandiagrammen exact de netwerken zoals in afbeelding 5 die een betegeling beschrijven!
Kortom: de quantumtheorie van toevalsmatrices is een quantumtheorie van netwerken, daarmee een quantumtheorie van betegelingen, daarmee een quantumtheorie van metrieken, en daarmee dus een quantumtheorie van de tweedimensionale zwaartekracht… een flink aantal stappen, maar met een verrassend en heel erg nuttig resultaat. Hiermee hebben we opnieuw een interessante toepassing van matrices binnen de natuurkunde gezien. De zoektocht naar een quantumbeschrijving van zwaartekracht heeft ons geleid naar een vereenvoudigd model van ons universum met maar één ruimtelijke dimensie. Hoewel deze modellen misschien wat gek aandoen, blijken ze een fijn speelveld om het probleem van quantumzwaartekracht te bestuderen. De meetkundige beschrijving van zwaartekracht en de formulering van de quantumfysica in termen van kansberekening komen op een mooie manier samen in het begrip toevalsoppervlak. Het feit dat we dingen kunnen berekenen in dit model volgt uit verassende connectie met toevalsmatrices. Toevalsmatrices zijn een onmisbaar stuk gereedschap in de quantumfysica – en dat is dan weer beslist geen toeval!