
Een beschrijving van de theoretische fysica is uiteraard niet volledig zonder uit te wijden over haar iets minder bekende zusje: de mathematische fysica. De argeloze lezer vraagt zich wellicht af: hoezo mathematisch? Is de theoretische discipline niet al meer dan wiskundig genoeg? In deze onschuldige vraag dient zich een heuristische definitie aan: een mathematisch fysicus is iemand voor wie het antwoord op bovenstaande vraag `nee!’ is. Het staat buiten kijf dat de theoretische natuurkunde al eeuwenlang grootafnemer van zuivere wiskunde is, en dat andersom die eerste een niet te onderschatten inspiratiebron is en blijft voor de tweede. De wiskundige bagage die bijvoorbeeld een snaartheoreticus absoluut nodig heeft in haar werk is indrukwekkend te noemen; zonder gedegen kennis van ingewikkelde machinerie als differentiaalmeetkunde, representatietheorie, Lie-theorie, functionaalanalyse en (algebraïsche) topologie is zij nergens. Aan de andere kant: een theoreticus blijft vooral een fysicus. Zij gebruikt haar wiskundige toolkit om natuurkunde te doen en zal, gewapend met haar fysische intuïtie, genoegen nemen met minder precieze argumenten en wiskundige inconsistenties. Dit is precies waar het verschil met een mathematische fysicus zit; mathematische fysica is wiskunde – met dezelfde hoge eisen aan precieze redeneringen en bewijzen – die zich bezighoudt met theoretische natuurkunde. Theoretische natuurkunde in de mal van de wiskunde gieten is minder mediageniek maar levert niet zelden prachtige wiskunde op die later op haar beurt op onverwachte wijze weer van essentieel belang in nieuwe natuurkunde blijkt te zijn. Een voorbeeld: de eeuwenoude wetten van Newton en Hamilton gaven in de 20e eeuw aanleiding tot het bestuderen van Hamiltoniaanse dynamica en symplectische meetkunde, zeer complexe en diepe deelgebieden die een centrale positie innemen in de hedendaagse analyse en differentiaal- en algebraïsche meetkunde, én hoofdrolspelers zijn in state-of-the-art snaar- en braanmodellen van quantumzwaartekracht, bij uitstek 21e-eeuwse natuurkunde!
Let wel, deze scheiding tussen theoretische en mathematische fysica is af en toe vaag en soms zeer artificieel: snaartheorie is zo mathematisch complex dat je haar beoefenaars vaak prima als mathematisch fysici kan bestempelen.
In het beschrijven van de wiskunde die op natuurlijke wijze opduikt in de theoretische natuurkunde is dus voor mathematische fysica bij uitstek een sleutelrol weggelegd, maar in dit artikel zullen we trachten licht te schijnen op een veel onverwachter (en spannender) tak van mathematische fysica: kunnen we natuurkundige theorieën loslaten op problemen in de zuivere wiskunde die alle beproefde methodes weerstaan? De natuurkunde helpt dan de wiskunde, in plaats van andersom.
Het voorbeeld dat we hier bespreken heeft natuurkundige en wiskundige aspecten die, zoals zo vaak, twee kanten van dezelfde medaille blijken te zijn.
Knopentheorie
Knopen worden al eeuwenlang bestudeerd in de wiskunde. Let wel: een wiskundige knoop heeft geen uiteinde. In wiskundig jargon is een knoop precies een cirkel ingebed in driedimensionale ruimte. Intuïtief is het logisch dat als je een knoop beweegt zonder een van de strengen door te knippen, je de knoop eigenlijk niet verandert. De exacte wiskundige realisatie van dit idee noemen we een ambiënte isotopie . Inderdaad, minstens de helft van de complexiteit zit in het taaltje dat wiskundigen spreken. Merk op dat de lus in je schoenveters (met de uiteinden aan elkaar vast gemaakt, anders is het geen wiskundige knoop) niet écht verknoopt is; deze raakt immers los als je eraan trekt, en dit is een ambiënte isotopie.
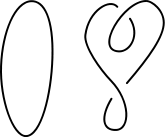
Afbeelding 1.De onknoop en een knoop die ambiënt isotoop is aan (“eigenlijk hetzelfde is als”) de onknoop.
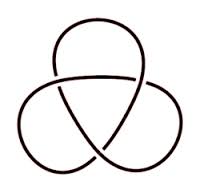
Afbeelding 2.De trefoil-knoop. Je ziet dat deze niet equivalent is aan de onknoop: we kunnen de trefoil níet ontknopen.
Hoewel een knoop inherent een object in een driedimensionale ruimte is kunnen we alle informatie in een knoop slim tweedimenisonaal representeren, als we maar precies aangeven voor elke kruising welke streng boven en onderlangs gaat, zoals aangegeven in de knoopdiagrammen hierboven.
Dé centrale probleemstelling in de knopentheorie, de uitdaging die aanstichter is van alle wiskundige progressie in dit vakgebied, is de volgende: bepaal voor twee willekeurige knopen of ze hetzelfde zijn of niet (en met hetzelfde bedoelen we uiteraard ambiënt isotoop). Dit is heel, héél erg moeilijk. Bekijk, om een voorzichtige indicatie te krijgen van hoe complex dit onschuldig klinkende probleem is, de volgende knoop.
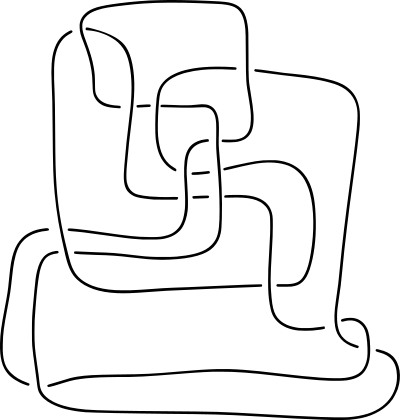
Afbeelding 3. Thistlethwaite-knoop.
Deze ingewikkelde “Thistlethwaite-knoop” is eigenlijk equivalent aan de onknoop, de niet-verknoopte cirkel!
De situatie is gelukkig niet hopeloos. De Duitse wiskundige Kurt Reidemeister bewees in een briljant werk, al in 1926, dat twee knopen alleen aan elkaar equivalent zijn als je de één uit de ander kunt verkrijgen door op de ander een eindige reeks van drie locale operaties toe te passen. Deze Reidemeister moves zien er zo uit:
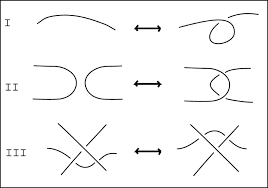
Afbeelding 3. Reidemeister moves. Source: “KnotPad: Visualizing and Exploring Knot Theory with Fluid Reidemeister Moves”, IEEE Transactions on Visualization & Computer Graphics, Dec. 2012
Dit geeft ons uiteraard nog geen classificatie van alle knopen, maar maakt het probleem wel behapbaar. We weten nu precies wat we moeten controleren om te concluderen dat twee knopen ambiënt isotoop zijn.
Onze centrale probleemstelling – classificeer alle knopen- blijkt een tikje te ambitieus, dus we pakken een simpeler (maar nog steeds extreem complex) probleem aan: we pogen een manier te vinden om uit te maken wanneer twee knopen zeker niet hetzelfde zijn.
Schetsmatig is het idee het volgende. We kennen aan elke knoop een algebraïsch object toe dat we praktisch kunnen uitrekenen, een getal of een polynoom, zodat dit object hetzelfde is voor ambiënt isotope knopen. Als we dit object (in ons geval altijd een polynoom) uitrekenen voor twee knopen, en het resultaat is niet hetzelfde, moeten we concluderen dat de knopen ook niet equivalent kunnen zijn. Zo’n polynoom dat hetzelfde is voor ambiënt isotope knopen noemen we een knoopinvariant. Bedenk ook dat als we eenmaal een knooppolynoom gedefinieerd hebben (we zullen straks zien hoe je zoiets doet) we alleen hoeven te checken dat het polynoom niet verandert als we de drie Reidemeister moves toepassen om na te gaan dat het polynoom daadwerkelijk een knoopinvariant is.
Het Jones-polynoom en Chern Simons-quantumveldentheorie
Knoopinvarianten klinken veelbelovend, maar het is op dit punt nog helemaal niet duidelijk dat dit soort invariante knooppolynomen überhaupt bestaan en interessant genoeg zijn. (Je kan natuurlijk het constante polynoom ‘0’ toekennen aan elke knoop. Dit is vanzelfsprekend een invariant, maar vertelt ons niets.). Ook dit is heel lastig. Het eerste interessante voorbeeld van een knooppolynoom is pas ontdekt in 1984 door Vaughan Jones: het naar hem vernoemde Jones-polynoom. Het is in essentie vrij eenvoudig te beschrijven wat het Jones-polynoom precies doet: ken aan de onknoop het constante polynoom ‘1’ toe, en leg de voorwaarde op dat voor drie knopen L+, L- en L0 die locaal verschillen als de Jones-polynomen V(L+), V(L-) en V(L0) voldoen aan de strengrelatie:
![]() ,
,
waarbij t de onafhankelijke variabele van het polynoom is. Doe dit vooral zelf thuis: probeer het Jones-polynoom van de trefoil-knoop uit te rekenen. Dit is niet constant ‘1’, dus de trefoil kan niet stiekem de onknoop zijn! Dit wisten we natuurlijk al, maar voor ingewikkeldere knopen is het Jones-polynoom een heel krachtige tool om ze van elkaar te onderscheiden.
Het bewijs van Jones dat deze procedure inderdaad een knoopinvariant geeft is heel ingewikkeld, en zijn constructie geeft ook geen hints hoe we andere, wellicht betere knoopinvarianten kunnen maken.
Is er misschien een slimmere manier om systematisch knoopinvarianten te vinden? Die is er inderdaad, en maakt gebruik van theoretische fysica!
Elders op deze site kan je lezen dat een enorm deel van de hedendaagse fysica berust op quantumveldentheorie. De centrale objecten in dit soort theorieën zijn velden die aan quantumwetten voldoen; we interpreteren de excitaties, de ‘trillingen’ van deze velden, als quantumdeeltjes. Zoals je misschien weet kunnen we alleen kansen toekennen aan natuurkundige processen in de quantumtheorie: nooit is met volledige zekerheid te zeggen op welke manier het proces of de interactie precies zal plaatsvinden. Eén van de interessante dingen die natuurkundigen in een quantumveldentheorie kunnen uitrekenen is de kans dat een excitatie, het bijbehorende quantumdeeltje dus, van punt A naar punt B beweegt in de lege ruimte (het vacuüm) waarin de quantumtheorie werkt.
We maken nu de connectie met knopen. Neem een of andere knoop, en herinner je dat deze in de driedimensionale ruimte leeft. In drie dimensies bestaat er een specifieke quantumveldentheorie, de zogenaamde Chern-Simonstheorie, die natuurkundigen heel goed begrijpen. We kunnen dus de kans berekenen dat een quantumdeeltje, waarvan de quantumwetten gecontroleerd worden door de Chern-Simonstheorie, precies langs de knoop beweegt door het vacuüm. Het prachtige en onverwachte resultaat is nu dat voor een specifieke variant van de Chern-Simonstheorie, deze kans exact het Jonespolynoom is van de knoop! Deze kans is in principe alleen een interessant natuurkundig object, maar heeft dus een interpretatie als heel diepe invariant in de knopentheorie. Blijkbaar is de Chern-Simonstheorie heel goed in het slim organiseren van wiskundige informatie over knopen!
Dit briljante inzicht uit het einde van de jaren ‘80 staat op naam van Edward Witten en Maxim Kontsevich, de belangrijkste namen in de mathematische fysica van de laatste 30 jaar. Als je geïnteresseerd bent in deze natuurkunde en wiskunde zal je ze ongetwijfeld vaker tegenkomen.
Het idee dat we hier zeer rudimentair hebben uitgelegd is veel verder uitgewerkt aan het eind van de jaren ’80 en begin van de jaren ’90 door mathematisch fysici als Nicolai Reshetikhin, Vladimir Drinfeld en Vladimir Turaev. Door verschillende symmetrieën toe te laten vinden we allerlei verschillende varianten van de Chern-Simonstheorie, die allemaal hun eigen knooppolynomen hebben. Zo geeft deze diepe connectie met theoretische fysica op een systematische manier een enorme hoeveelheid nieuwe knoopinvarianten, die toepasselijk quantuminvarianten worden genoemd.
Het uitdiepen van dit soort verrassende verbanden tussen natuurkundige ideeën en zuivere wiskunde is typische mathematische fysica.