Op het moment dat licht je ogen bereikt, is het al vele malen in aanraking gekomen met de moleculen in de lucht of bijvoorbeeld de atomen in een ruit. Door die interacties verandert het licht telkens van richting. Die verandering van richting hangt af van het soort materiaal. De grootheid die we hiervoor gebruiken noemen we de brekingsindex. Deze grootheid is gelijk aan 1 als er geen sprake is van een richtingsverandering, zoals in het vacuüm, maar ongelijk aan 1 als het licht wordt afgebogen, bijvoorbeeld als licht door glas gaat. De relatie die de richtingsverandering relateert aan de brekingsindex is de wet van Snellius:
n1 Sin(θ1) = n2 Sin(θ2).
Hierin zijn n1 en n2 de brekingsindices van medium 1 en medium 2 en de hoeken θ1 en θ2 zoals aangegeven in de figuur hieronder.
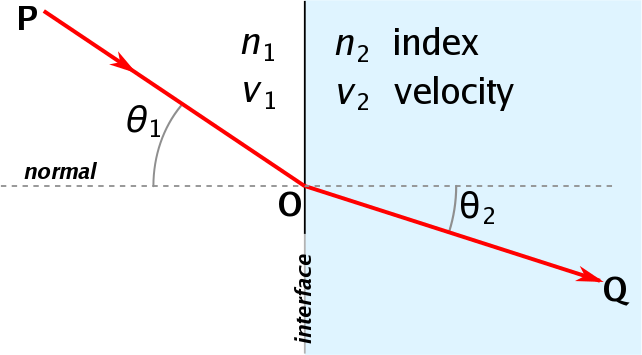
Afbeelding 1. Breking van lichtDoor de verandering van brekingsindex gaat licht breken; het verandert van richting.
De wet van Snellius kan afgeleid worden uit de Maxwellvergelijkingen. Deze prachtige vergelijkingen beschrijven elektromagnetisme en daarmee ook de interactie tussen licht en atomen. Met behulp van deze vergelijkingen hoeven we niet precies te weten hoe licht met elk individueel atoom botst, maar kunnen we kijken naar een gemiddelde van al die botsingen. Dit is maar goed ook, want anders zouden we, vanwege de enorme hoeveelheid atomen in een stukje materie, theoretisch gezien vrijwel niets kunnen uitrekenen. De brekingsindex is dus een effectieve manier om de interactie van licht en materie te beschrijven.
Voor de meeste materialen die we in de natuur tegenkomen is de brekingsindex een positief getal. Dit betekent dat een lichtstraal met een bepaalde richting min of meer dezelfde richting aanhoudt als het door een stukje glas gaat. Een negatieve brekingsindex komt niet in de natuur voor, maar is niet verboden volgens de Maxwellvergelijkingen. Het zou dus in principe mogelijk moeten zijn om zulke materialen te maken!
In het jaar 2000 is het Amerikaanse onderzoekers gelukt om een dergelijk materiaal te maken. Als licht door dit materiaal reist, zal het wel een grote richtingsverandering ondergaan. Een rietje in een glas water met negatieve brekingsindex, gaat er dan heel gek uit zien en lijkt gebroken te zijn. Een simulatie van deze hypothetische situatie is hieronder weergegeven.

Afbeelding 2. Negatieve brekingsindexVloeistof met een rietje erin. Links heeft de vloeistof een negatieve brekingsindex, terwijl het rechter glas normaal water bevat. Foto: Tiffany C. Inglis
Materialen zoals deze, ook wel metamaterialen genoemd, zijn niet alleen interessant vanuit een theoretisch oogpunt. Ook praktisch gezien zijn ze veel belovend. De wetenschapper prof. sir John Pendry beschreef in een artikel uit 2000 bijvoorbeeld dat een lens gemaakt van een materiaal met negatieve brekingsindex bijna perfect kan zijn en niet gelimiteerd is door de golflengte van licht. Vier jaar later werd zo’n lens inderdaad gebouwd, en bleek die drie keer zo goed te werken als voorheen mogelijk was. Het enige nadeel van deze lens is dat hij zo goed werkt voor microgolven, maar niet voor zichtbaar licht. Zou een dergelijke lens voor licht van andere golflengtes ook geproduceerd kunnen worden, dan is dit goed nieuws voor bedrijven als ASML, omdat zulke lenzen in de machines waarin chips gemaakt worden voor nog kleinere transistoren zouden kunnen zorgen, en daarmee voor nog krachtigere elektronica.
We hebben in dit stuk nog maar het oppervlak van alle mogelijke metamaterialen bekeken. Er zijn vele variaties mogelijk, sommigen nog exotischer dan anderen. Zo zijn er bijvoorbeeld ook metamaterialen die ervoor kunnen zorgen dat het licht om een object heen wordt gebogen waardoor het onzichtbaar lijkt. Dat lijkt een eerste stap naar een echte onzichtbaarheidsmantel zoals in de Harry Potterfilms. In een volgend artikel zullen we meer van dit soort fascinerende natuurkunde bekijken en zien hoe licht en materie met elkaar wisselwerken.