
Afbeelding 1. Een donutplaneet.Artistieke impressie van hoe de aarde er zou kunnen uitzien als hij de vorm van een torus (donut) had, al zouden in werkelijkheid de atmosfeer en de geologie drastisch anders zijn dan hier afgebeeld. (Bron: screenshot YouTubefilmpje LifesBiggestQuestions, via vice.com.)
Eerst iets over de precieze vorm en vorming van zo’n absurde planeet. Het is belangrijk te beseffen dat materie op de schaal van planeten zich in essentie als een vloeistof gedraagt: de inherente kracht van welk mineraal of metaal dan ook is vele malen te klein om de zwaartekracht in de richting van het centrale punt te weerstaan. Er moet dus een andere kracht aan het werk zijn die ervoor zorgt dat de materie zich niet verzamelt rond het middelpunt en een “saaie” bolvormige planeet vormt. Deze kracht (technisch gezien een ‘schijnkracht’) ervaar je wanneer je een rondje op de draaimolen zit: centrifugale kracht. De centrifugale (of: middelpuntvliedende) kracht werkt van het middelpunt áf, wat onder de juiste omstandigheden precies de zwaartekracht kan compenseren. Dat toonde Henri Poincaré in 1885 al aan in een behandeling van allerlei roterende lichamen.
Rudimentaire simulaties tonen aan dat de meeste donutvormige hemellichamen alsnog binnen de kortste keren uiteen zouden spatten of een afgeplatte bol zouden vormen. Sommige zijn echter wel stabiel: bijvoorbeeld een torus met een massa die zes keer zo groot is als die van de aarde, een oost-westomtrek van meer dan drie keer die van de aarde, een noord-zuidomtrek van bijna 80%, en het voornaamste: een omwentelingstijd van slechts 3,5 uur. De versnelling die een persoon op het oppervlak van een dergelijke planeet voelt, is ook een combinatie van de twee krachten die de planeet vorm hebben gegeven, en is sterk afhankelijk van de plaats waarop deze persoon zich bevindt – zie afbeelding 2. Opvallend is dat je het zwaarst bent net een beetje aan de binnenkant van de ‘polen’ van de torus. Dat is onder andere het gevolg van het feit dat de doorsnede van de torus eivormig is, en dus niet precies rond.
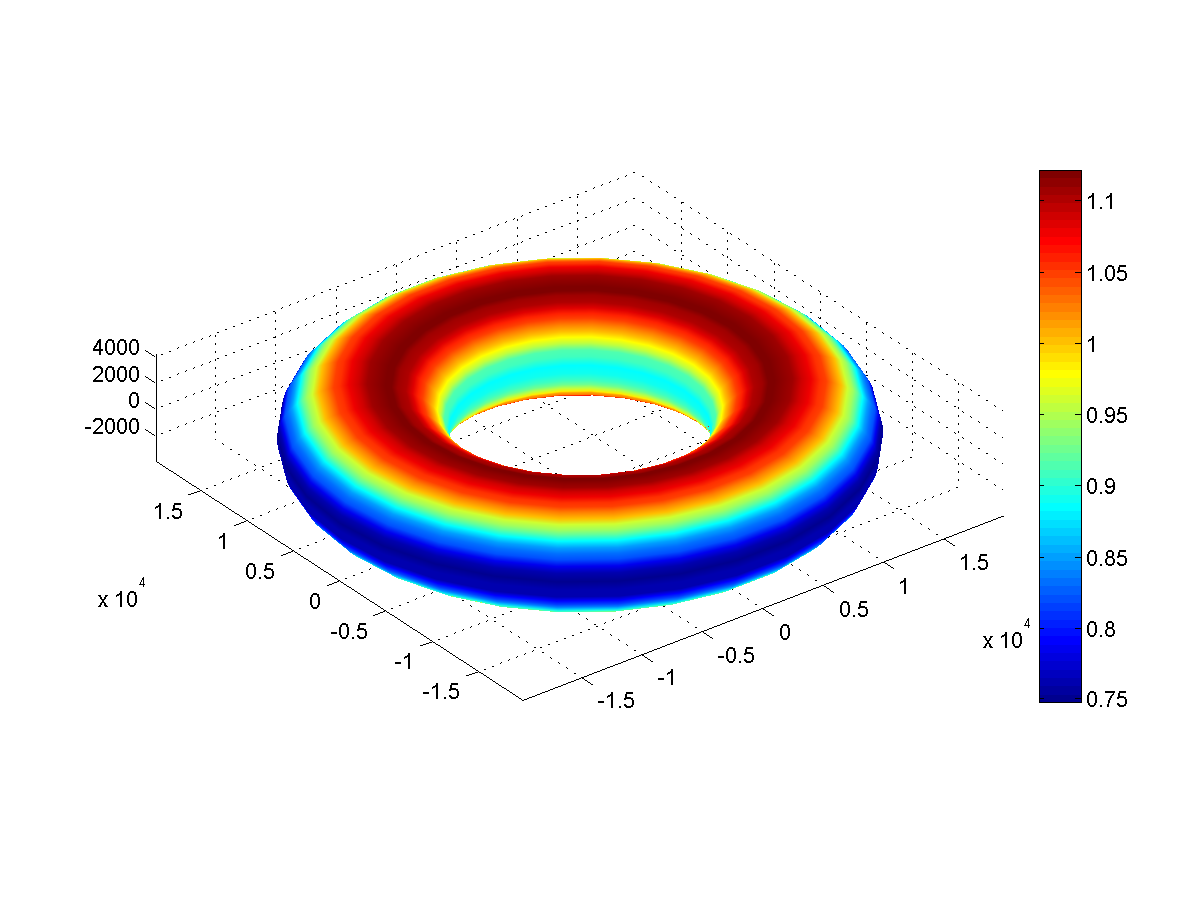
Afbeelding 2. Zwaartekracht op een donutplaneet.De valversnelling op een stabiele torus, gemeten als veelvoud van de versnelling op aarde (9,81 m/s2). Door van pool naar buitenste evenaar te lopen, kan je meer dan een kwart van je gewicht verliezen! (Bron: Anders Sandberg in Gizmodo.)
De volgende vraag die we onszelf kunnen stellen, is welke klimaateffecten deze bizarre fantasieplaneet in petto heeft. Ten eerste zijn, zoals vermeld, de dagen met 3,5 uur veel korter dan op aarde. De vermoedelijk hallucinante helrode zonsopgang langs de binnenkant van de ring, waar de zon na anderhalf uur nacht terug langs de enorme boog in zicht gebracht wordt, staat na enkele minuten al vele graden boven de horizon. Dat wil zeggen: als de zon natuurlijk überhaupt nog boven de bergketens uitkomt; omwille van het feit dat continenten in hun tektonische drift naar het centrum enorm moeten inkrimpen om te kunnen passen, valt te verwachten dat het op onze planeet krioelt van de stenen mastodonten, die door de relatief lage zwaartekracht ook nog eens veel trager afbrokkelen. Gelukkig zijn de nachten tussen die ijzige pieken helemaal zo donker niet: het licht dat op de planeet aan de andere kant van het centrale gat gereflecteerd wordt, is zo helder dat van “nacht” amper sprake kan zijn. Let op: we zijn ervan uitgegaan dat ook van deze planeet, net als bij de aarde, de draaias onder een hoek van 23 graden op het baanvlak rond de centrale ster staat. Is die hoek echter minder dan een paar graden, dan heerst in de binnenzone een permanente nacht, en is het bestaan van een vuurbal in de lucht een mythe afkomstig van verdwaalde reizigers uit de buitenregionen.
Nog interessanter wordt het wanneer we gaan kijken naar de baan die een satelliet (zoals een maan) kan volgen rond dit topologisch kunstwerk. Helaas maar waar: hoe mooi het ook zou zijn, een zwevende maan in het middelpunt is uitgesloten. Dit is immers een zogenaamd “instabiel Lagrange-punt”; wiskundig gezien kan hier wel een voorwerp zweven, maar elke afwijking van het exacte middelpunt zal worden uitvergroot totdat de maan tussen de bergen belandt. Andere, wel degelijk mogelijke banen zijn evenwel minstens zo opmerkelijk: simulaties tonen bijvoorbeeld aan dat een maan op en neer zou kunnen vliegen, precies door het Lagrange-punt heen! Ook kan een satelliet een “vaaspatroon” beschrijven, of zelfs een 8-vorm in precessie – zie afbeelding 3.
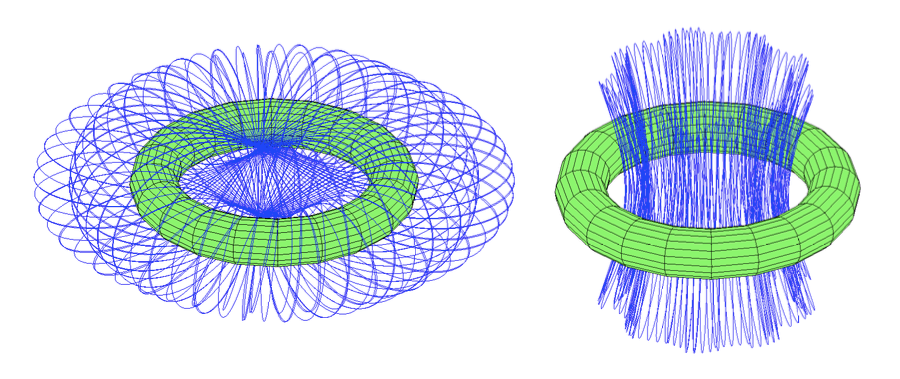
Afbeelding 3. Bijzondere banen.Enkele satellietbanen die volgens rudimentaire simulaties toegestaan zijn. Links: een maan legt een 8-vorm af door het gat van de torus, en voert daarbij ook een precessie uit die de vorm van de planeet volgt. Rechts: een “vaasvormige” baan, iets wat op het eerste gezicht onmogelijk lijkt. (Bron: Anders Sandberg in Gizmodo.)
Realistischer zijn toch banen die we herkennen van onze eigen maan: rond de planeet. Nog steeds zijn de banen van een dergelijke maan een stuk exotischer dan de onze. Kijk bijvoorbeeld naar de maan in het equatoriale vlak van de planeet: een baan met een enorme ellipticiteit die bovendien opnieuw een precessie vertoont en zo een knappe rozet beschrijft – afbeelding 4. Ondanks het feit dat dit de meest met onze ervaring overeenkomende omwenteling is, is ook deze baan waarschijnlijk op de lange termijn instabiel als gevolg van getijdekrachten (die in de simulaties niet werden meegenomen). Spijtig genoeg wint de realiteit het ook hier van de schoonheid.
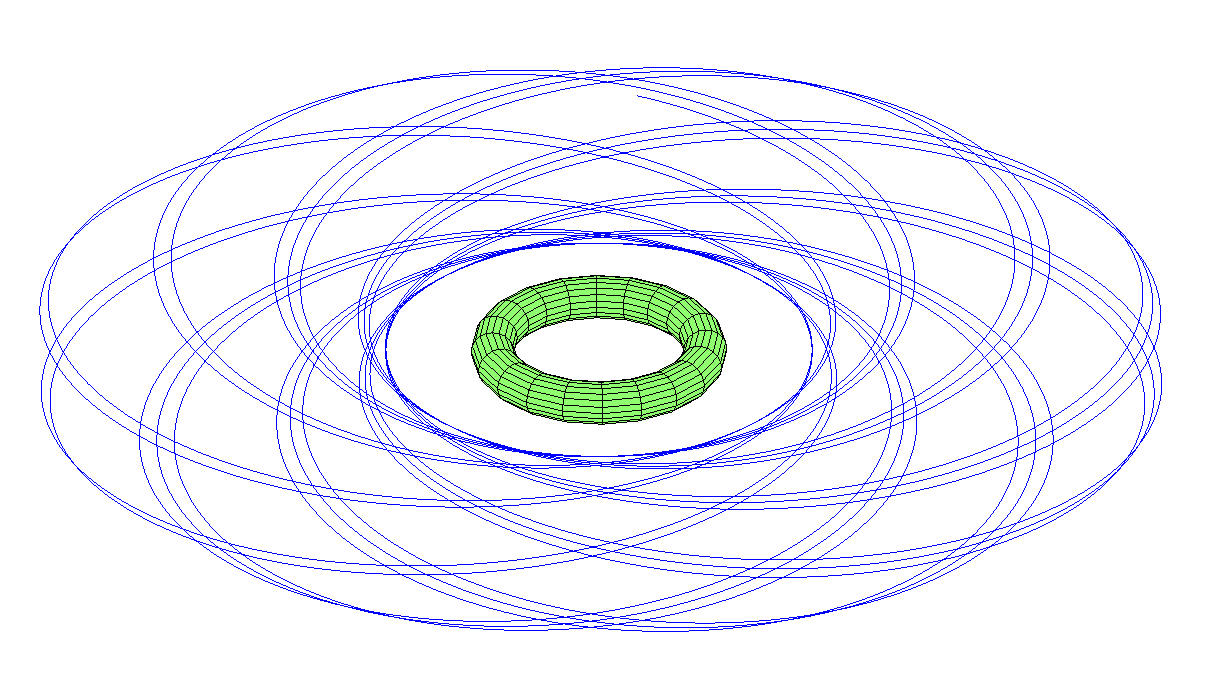
Afbeelding 4. Een “gewone” baan.Een maan die in het equatoriale vlak een rozet beschrijft. (Bron: Anders Sandberg in Gizmodo.)
Titanische cyclonen, klimaatbanden zoals op het oppervlak van Jupiter, krankzinnige geologische activiteit, ingewikkelde magnetische velden… er zijn nog tal van eigenschappen van onze hypothetische ringwereld die ik hier niet besproken heb maar waarover wild – maar beredeneerd – gespeculeerd kan worden. Naast het feit dat je door het bestuderen van zo’n exotische mogelijkheid het nodige kan leren over de situatie hier op onze gezonde ronde grond, is het vooral leuk om de technieken van de natuur- en wiskunde te gebruiken om onze fantasie binnen de grenzen daarvan de vrije loop te laten. Ooit zullen die technieken ons misschien in staat stellen om zodanig geavanceerde simulaties te ontwikkelen dat speculaties antwoorden worden. In de tussentijd dromen we rustig verder van groene wezens ergens op een donutplaneet die, onder het smullen van besuikerde bollen gefrituurd deeg, discussiëren over hoe het leven op een ronde planeet zou zijn.
Lees voor meer informatie over dit onderwerp het artikel van Anders Sandberg op Gizmodo waarop veel kennis over toruswerelden werd ontleend: “What would the Earth be like if it was the shape of a donut?”, of kijk het filmpje “If Planets Were Donuts” van YouTuber Artifexian. De fundamenten van symmetrie en evenwicht worden op YouTube dan weer toegelicht door het uitstekende PBS Space Time in een clipje dat de naam “Why is the Earth Round and the Milky Way Flat?” draagt. Het artikel van Henri Poincaré dat in de tekst werd vermeld heet “Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation”, werd gepubliceerd in 1885 en is gratis online beschikbaar.