
Afbeelding 1. Een sneeuwkristal.Een sneeuwkristal bij een sterke vergroting onder een rasterelektronenmicroscoop. Afbeelding: Electron and Confocal Microscopy Laboratory, US Department of Agriculture (Wikipedia).
Heerlijk symmetrisch
Kristallen zijn natuurkundig mooie systemen omdat ze wiskundig simpel beschreven kunnen worden. Dit is in tegenstelling tot amorfe stoffen, wat harde stoffen zijn die van binnen níet geordend zijn; het bekendste voorbeeld daarvan is glas. Een kristal bevat twee belangrijke soorten symmetrieën: translatiesymmetrie en interne symmetrieën. De eerste symmetrie zit in de periodiciteit (het herhalingspatroon) van een kristalrooster. De ‘bouwstenen’ van een kristal zijn zogeheten eenheidscellen die op elkaar gestapeld zijn, als een soort legoblokjes. Iedere eenheidscel is precies hetzelfde is als alle andere, dus als je het hele kristal een eenheidscel opschuift, blijft het rooster precies hetzelfde: dit is translatiesymmetrie. Auguste Bravais liet in 1848 al zien dat er in drie dimensies maar 14 soorten eenheidscellen mogelijk zijn: de Bravaistralies (afbeelding 2). Op de positie van de ‘bollen’ in de afbeelding kunnen zich atomen, ionen of moleculen bevinden. Een kristal van tafelzout is bijvoorbeeld opgebouwd uit de ionen Na+ en Cl–, terwijl een ijsblokje is opgebouwd uit watermoleculen.
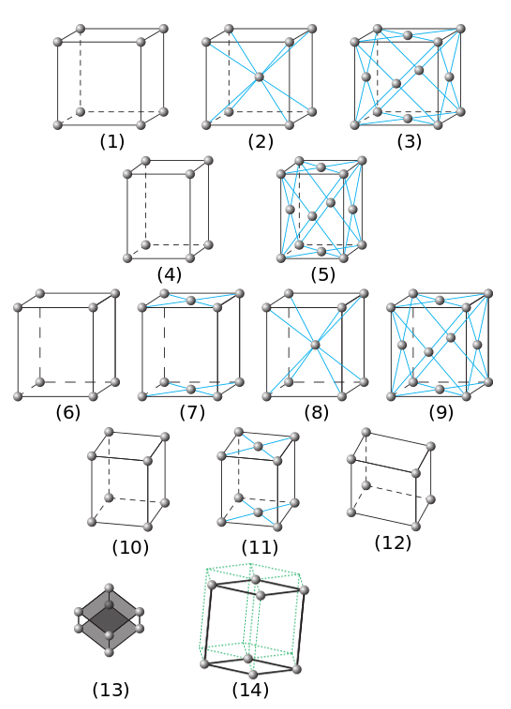
Afbeelding 2. De Bravaistralies.Alle mogelijke ‘bouwstenen’ van een kristal: de 14 Bravaistralies. Als je deze bouwstenen opstapelt, heb je een kristal! Afbeelding: Wikipediagebruiker Napy1kenobi.
Behalve translatiesymmetrie hebben de bouwstenen van een kristal zelf interne symmetrieën. Neem als voorbeeld hiervoor een simpel kubisch tralie (afbeelding 3). De posities van de bollen blijven hetzelfde als je het rooster spiegelt in het blauwe vlak, een kwartslag roteert om de as loodrecht op het oranje vlak, of inverteert (of puntspiegelt) in het groene punt in het midden van de kubus. Het tralie heeft dus spiegelsymmetrie, (4-voudige) rotatiesymmetrie, en inversiesymmetrie.
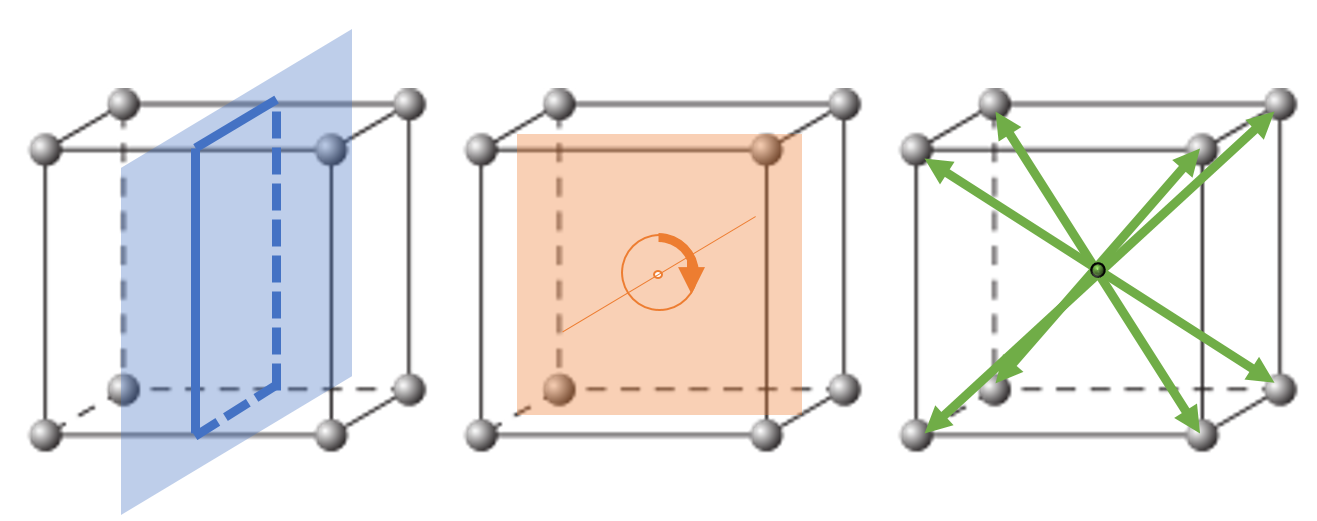
Afbeelding 3. Symmetrieën van een kubisch tralie.Interne symmetrieën: spiegeling (blauw), rotatie (oranje) en inversie (groen).
Aan de regels houden
De Bravaistralies laten zien dat kristallen alleen maar bepaalde rotatie-symmetrieën kunnen hebben, namelijk 2-, 3-, 4-, of 6-voudig. Een kubisch rooster (zoals (1) in afbeelding 2) heeft bijvoorbeeld 2-, 3- en 4-voudige rotatiesymmetrie, en een hexagonaal rooster (zoals (14) in afbeelding 1) heeft 2-, 3- en 6-voudige rotatiesymmetrie. (Kun je dit zelf inzien? Pak er anders een dobbelsteen bij, of knip een zeshoek uit een stuk papier, en draai ze maar eens rond.) De sneeuwvlok in afbeelding 1 heeft een 6-voudige rotatiesymmetrie, waardoor je kunt zien dat het kristalrooster hexagonaal is.
Je vraagt je misschien af waarom een 5-voudige rotatiesymmetrie dan niet kan. Dit kun je voor jezelf uittekenen in twee dimensies, als je begint met een enkele regelmatige vijfhoek. Probeer er nu maar soortgelijke vijfhoeken aan vast te plakken zonder dat je gaten in het tweedimensionale rooster introduceert. Je zult al snel merken dat dit niet lukt, want het past gewoon niet!
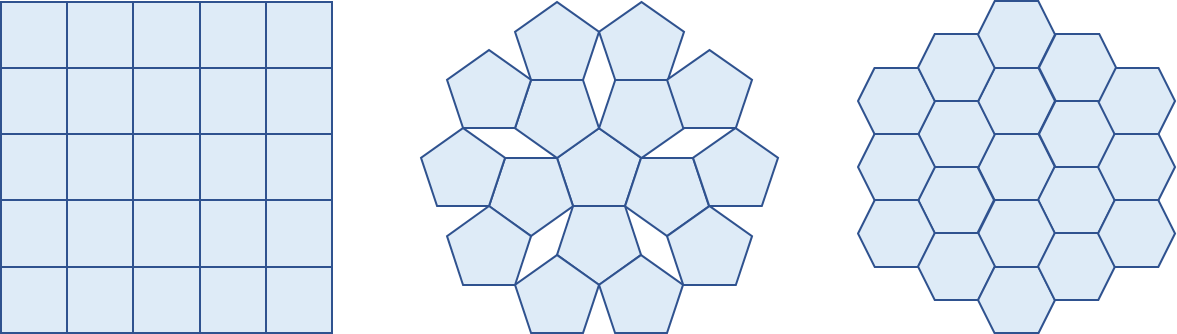
Afbeelding 4. Tweedimensionale roosters.Tweedimensionale roosters met (v.l.n.r) 4-, 5-, en 6-voudige rotatiesymmetrie. Een rooster opgebouwd uit vijfhoeken kan niet zonder gaten gemaakt worden, en kan dus ook geen kristal vormen.
Quasikristallen
De wiskundig fysicus Roger Penrose bestudeerde in de jaren ’70 tweedimensionale niet-periodieke roosters, opgebouwd uit twee of meer soorten ‘tegels’. Hij bewees hiermee dat het mogelijk is om een tweedimensionaal vlak te vullen (zonder gaten) met deze tegels, op zo’n manier dat het een 5-voudige rotatiesymmetrie bevat, en zelfs ook een spiegelsymmetrie, maar géén translatiesymmetrie. Afbeelding 5 is hier een voorbeeld van: door het rooster een vijfde slag (72 graden) rond te draaien, of door het in een verticale lijn door het midden te spiegelen, verander je niets, maar er is geen manier om het vlak naar rechts of links te schuiven zodat alle tegels weer bovenop elkaar vallen. Hoewel het wel geordend is, is het rooster zonder translatiesymmetrie niet periodiek, en kan het dus ook niet als (tweedimensionaal) kristal beschouwd worden! Dit noemen we een quasikristal, met het Latijnse voorvoegsel “quasi-” dat “alsof” betekent.
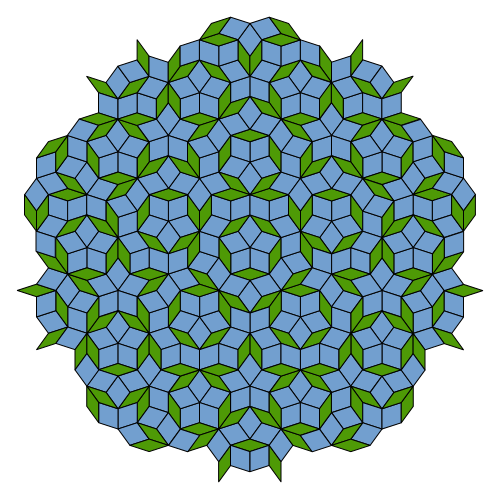
Afbeelding 5. Een Penrose-betegeling.Een Penrose-betegeling. Deze betegeling heeft een 5-voudige rotatiesymmetrie en een spiegelsymmetrie, maar is niet kristallijn omdat het geen translatiesymmetrie bevat. Afbeelding: Wikipediagebruiker Inductiveload.
Wiskundig gezien zijn Penrose-betegelingen wel grappig, maar bestaan er ook driedimensionale quasikristallen? Je kunt je voorstellen dat je een normaal kristal kunt vormen door gewoon eenheidscellen een voor een aan elkaar vast te plakken, wat ook kan omdat alles makkelijk in elkaar past. In een quasikristal maakt de volgorde en manier waarop de verschillende eenheidscellen (zoals de tegels in afbeelding 5) aan elkaar geplakt zijn veel uit, want als het niet op de juiste manier gedaan wordt eindig je met een ongeordend (amorf) systeem. Zo werd er jarenlang in het veld van kristallografie gedacht dat quasikristallen niet in de natuur voor zouden komen.
Toch ontdekte Dan Shechtman op 8 april 1982 een materiaal met een 5-voudige rotatiesymmetrie. Pas in 1984 durfde hij het te publiceren, en zette hij hiermee de kristallografische wereld op zijn kop. In 2011 kreeg hij voor deze ontdekking de Nobelprijs voor de scheikunde, en tegenwoordig zijn er honderden voorbeelden van quasikristallen bekend. De meeste quasikristallen die bekend zijn worden gemaakt door een vloeibaar mengsel van metalen heel snel af te koelen, maar in 2010 werd ook het eerste natuurlijke quasikristal gevonden: het mineraal Al63Cu24Fe13. Dit mineraal komt waarschijnlijk uit een meteoriet die door het neerstorten op aarde heel snel afkoelde. Een quasikristal maken blijkt dus geen makkie!
