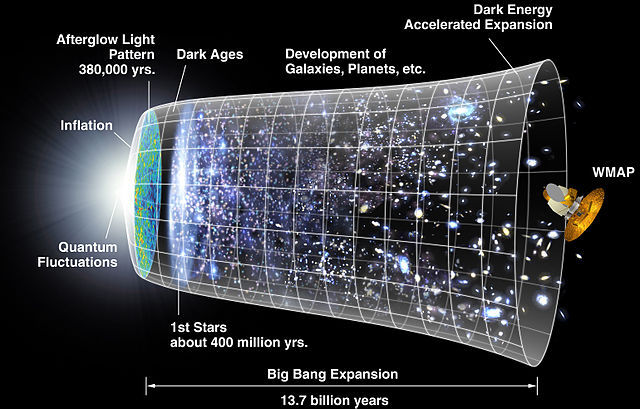
Afbeelding 1. De groei van het heelal.In deze afbeelding is schematisch de groei van het heelal in de loop van de geschiedenis weergegeven. Links zien we dat het vroege heelal enorm snel lijkt te zijn uitgedijd. Het bestaan van deze kosmische inflatie zou zowel het vlakheidsprobleem als het horizonprobleem kunnen oplossen. Afbeelding: NASA/WMAP.
Het vlakheidsprobleem
Volgens de algemene relativiteitstheorie van Albert Einstein moeten we de ruimte om ons heen (of eigenlijk zelfs: de ruimte en de tijd om ons heen) zien als een kneedbare, vervormbare substantie. Voor drie ruimtedimensies is die vervormbaarheid erg lastig voor te stellen, maar met een dimensie minder wordt dat makkelijker: het ‘speelveld’ van het heelal is geen groot, onvervormbaar, plat bord, maar valt beter te vergelijken met een groot stuk rubber, dat lokaal vervormd en gekromd kan worden.
Dat roept echter onmiddelijk een vraag op. Als we om ons heen het heelal in kijken, zien we nauwelijks iets van die vervorming. De ruimte om ons heen zou op grote schaal vervormd kunnen zijn, maar is dat nauwelijks. Dat valt ook heel precies te meten. Zie afbeelding 2 hieronder: in een platte ruimte is de som van drie hoeken van een driehoek 180 graden, maar in een gekromde ruimte is dat meer of minder. We kunnen hoeken meten tot aan de verste uithoeken in het heelal (hoe precies, dat wordt in de video hieronder uitgelegd), en het heelal lijkt extreem plat te zijn.
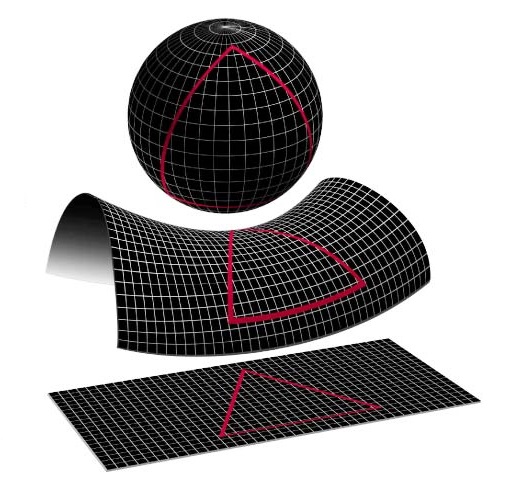
Afbeelding 2. Is het heelal plat?In een vlakke ruimte (onder) is de som van de drie hoeken van een driehoek altijd gelijk aan 180 graden. In een gekromde ruimte kan dat meer (boven) of minder (onder) zijn. Ons heelal lijkt een driedimensionale versie van het onderste plaatje te zijn. Afbeelding: NASA.
Is dat heel verbazend? Jazeker! Het blijkt namelijk dat eventuele kromming in het heelal zichzelf in de loop van de tijd versterkt. Als het heelal ook maar een klein beetje gekromd was begonnen, zou die kromming inmiddels gigantisch moeten zijn. Het heelal is dus niet alleen altijd al heel vlak geweest; het moet zelfs extreem vlak begonnen zijn om te kunnen verklaren dat het nu nog steeds zo vlak is. Hoe kan dat?
Het horizonprobleem
Een tweede raadsel in de kosmologie komen we tegen als we naar de verste uithoeken van het heelal kijken. Het licht dat we van deze enorm verre uithoeken ontvangen, heet de achtergrondstraling. Het is licht dat niet alleen van heel ver komt, maar ook heel oud is – het is immers heel lang onderweg geweest! Het opvallende aan dit licht is dat het er in alle richtingen vrijwel hetzelfde uitziet. Met andere woorden: alle extreem verre stukken heelal die wij zien, zijn vrijwel even warm, hebben vrijwel dezelfde dichtheid, enzovoort. Het vroege heelal was dus enorm homogeen.
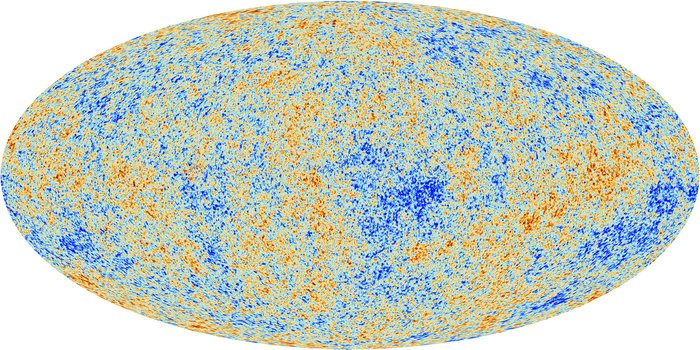
Afbeelding 3. De kosmische achtergrondstraling.Op deze “uitgerolde hemelkaart” zien we het licht dat we vanaf de verste afstanden in alle richtingen uit het heelal opvangen: de kosmische achtergrondstraling. Opvallend is dat het plaatje dat we zien enorm homogeen is. Om überhaupt lichte en donkere plekken te kunnen zien, moet het contrast gigantisch versterkt worden. In werkelijkheid is het verschil is temperatuur (een maat voor de “helderheid”) tussen de helderste en zwakste gebieden in de orde van 0,001%. Afbeelding: ESA.
Ook hier kunnen we weer vragen: is dat zo bijzonder? En ook hier is het antwoord: ja! Als we kijken naar twee verafgelegen stukken heelal in tegengestelde richtingen aan de hemel, bevinden deze gebieden zich immers gigantisch ver van elkaar af. Sterker nog: de afstand tussen die twee gebieden is zó groot, dat ze nog nooit met elkaar in contact zijn geweest! In de gehele leeftijd van het heelal heeft het licht – het allersnelste medium in het heelal – nog niet genoeg tijd gehad om vanuit het ene gebied het andere te bereiken. De gebieden hebben elkaar dus nooit kunnen zien of beïnvloeden: ze liggen niet binnen elkaars “horizon”.
Homogeniteit ontstaat echter uit interactie. Mijn kop thee krijgt, als ik die lang genoeg laat staan, dezelfde temperatuur als de kamer eromheen. Zonder zulke interactie is er geen enkele reden waarom een willekeurige kop thee en een willekeurige kamer dezelfde temperatuur zouden hebben. Waarom ziet het heelal er dan toch in alle richtingen hetzelfde uit?
Inflatie
Eén mogelijke oplossing voor dit probleem is het idee van inflatie. Wellicht is het hele heelal in een vroeg stadium van zijn bestaan met een enorme snelheid “opgeblazen” – zo snel dat het in een minieme fractie van een seconde vele machten van 10 groter werd. Dat zou zeker de vlakheid verklaren: wie een ballon opblaast, merkt ook dat het oppervlak daarvan steeds vlakker en vlakker wordt. Een enorm opgeblazen heelal zal dus ook plaatselijk enorm vlak zijn.
Ook het horizonprobleem wordt door het idee van inflatie opgelost. Twee gebieden kunnen immers vóór de periode van inflatie al uitgebreid met elkaar in contact zijn geweest, en daardoor met elkaar in evenwicht zijn gekomen, waarna inflatie ze op de gigantische afstand bracht die we vandaad de dag zien.
Maar wacht eens even… Betekent dat dan niet dat het heelal zelf sneller dan het licht moet zijn uitgedijd? Jazeker! Maar dat is natuurkundig gezien geen enkel probleem. Einstein toonde weliswaar aan dat niets sneller dan het licht door de ruimte kan bewegen, maar die ruimte zelf kan willekeurig snel vervormd worden. Vergelijk het weer met een stuk rubber: een mier die daar overheen loopt, kan dat maar met een bepaalde snelheid doen, maar intussen kunnen we het rubber zo snel uitrekken als we willen.
Meer weten over dit intrigerende idee van inflatie? Het Youtubekanaal PBS Space Time, waarvan we al eerder een video hebben geplaatst, maakte vorige week een aflevering over dit onderwerp. De video valt hieronder terug te kijken: